情感与信任关系结构方程模型修正结果

1.模型修正的思路

模型拟合指数和系数显著性检验固然重要，但对于数据分析更重要的是模型结论一定要具有理论依据，换言之，模型结果要可以被相关领域知识所解释。因此，在进行模型修正时主要考虑修正后的模型结果是否具有现实意义或理论价值，当模型效果很差时^[6]可以参考模型修正指标对模型进行调整。

当模型效果很差时，研究者可以根据初始模型的参数显著性结果和Amos 提供的模型修正指标进行模型扩展（Model Building）或模型限制（Model Trimming）。模型扩展是指通过释放部分限制路径或添加新路径，使模型结构更加合理，通常在提高模型拟合程度时使用；模型限制是指通过删除^[7]或限制部分路径，使模型结构更加简洁，通常在提高模型可识别性时使用。

Amos 提供了两种模型修正指标：修正指数（Modification Index）和临界比率（Critical Ratio）。^[8]

修正指数用于模型扩展，是指对于模型中某个受限制的参数，若容许自由估计（譬如在模型中添加某条路径），整个模型改良时将会减少的最小卡方值。^[9]使用修正指数修改模型时，原则上每次只修改一个参数，从最大值开始估算。但在实际中，也要考虑让该参数自由估计是否有理论依据。

临界比率用于模型限制，是计算模型中的每一对待估参数（路径系数或载荷系数）之差，并除以相应参数之差的标准差所构造出的统计量。在模型假设下，CR 统计量服从正态分布，所以可以根据CR 值判断两个待估参数间是否存在显著性差异。若两个待估参数间不存在显著性差异，则可以限定模型在估计时对这两个参数赋以相同的值。

2.本研究模型修正过程

在对本研究中，初始模型运算结果如表5-14，各项拟合指数尚可。但从模型参数的显著性检验中可发现：

表5-13　5%水平下不显著的估计参数

排除上面表5-10 中的路径系数在0.05 的水平下不显著外，该模型其他各个参数在0.05 水平下都是显著的，首先考虑去除p 值较大的路径，即结构方程部分中信任认知度（ξ1）和家庭情感关系（ξ3）对情感行为意向（η2）两条不显著的路径。由于家庭情感关系（ξ3）的结构方程部分的平方复相关系数为0.035，非常小。另外，从实际的角度考虑，考研学生一般都是即将毕业的学生，也就是在学校已经经历四年的学习生活，个人交往对象中多数是老师和同学，家庭的影响在此期间相比较弱，更重要的是，随着知识的增加，个人处事行为更理性，处世更成熟，因此感性行为出现较少。而信任认知度是明显的理性行为的表现，因此去掉其对情感行为意向的影响也是合理的。所以，考虑将两对潜变量的路径在本书的结构方程模型中去除。修改的模型如图5-6 所示：

图5-6　修正的模型一

表5-14　常用拟合指数计算结果

从表5-14 可以看出，卡方值几乎没变，但自由度增加了，并且各拟合指数有所提高，最重要的是模型变简单了，因此做此改变是值得的。修正后模型的各个参数在0.05 的水平下都是显著的，并且从实际考虑，各因子的各个路径也是合理存在的。(www.xing528.com)

下面考虑通过修正指数对模型修正，δ8 与δ11 的MI 值为5.768，表明如果增加δ8 与δ11 之间的残差相关的路径，则模型的卡方值会最少减小5.768。从实际考虑，“您与父亲的关系怎样”（Q24_1）与“个人的情感完全是自由的”（Q40d_1）之间也确实存在相关。设想一下，对个人而言，追求情感的自由很大程度上是受其家庭的影响，特别是中国的家庭一般是父亲主导管理的，因此我们在追求自由情感这一问题上，与父亲的关系较为显著。因此考虑增加δ8 与δ11 的相关性路径。（这里的分析不考虑潜变量因子可测指标的更改，理由是我们在设计问卷的题目的信度很好，而且题目本身的设计也不允许这样做，以下同）

重新估计模型，重新寻找MI 值较大的，δ4 与δ1 的MI 值较大，为4.041，表明如果增加δ4 与δ1 之间的残差相关的路径，则模型的卡方值会减小较多。这也是“您与同学的关系如何”（Q28_1）与“人与人之间应当相互信任”（Q40e_1）之间也确实存在相关，因此考虑增加δ4 与δ1 的相关性路径。另外，从剩下的变量之间MI 值没有可以做处理的变量，因此考虑MI 值修正后的模型如图5-7 所示：

表5-15　5%水平下不显著的协方差相关路径

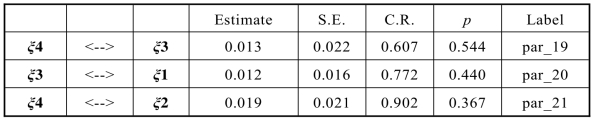
除上面表5-15 中的路径系数在0.05 的水平下不显著外，该模型其他各个协方差参数估计在0.05 水平下都是显著的，考虑依次去除p 值较大的路径，即结构方程部分中情感认知度（ξ4）与家庭情感关系（ξ3）、信任认知度（ξ1）与家庭情感关系（ξ3）、情感认知度（ξ4）与学习情感关系（ξ2）之间的路径。修改的模型如图5-8 所示：

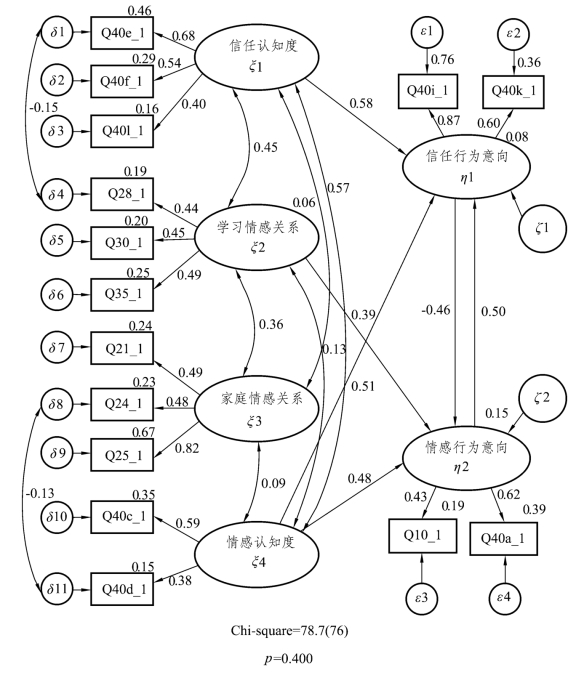
图5-7　修正的模型二

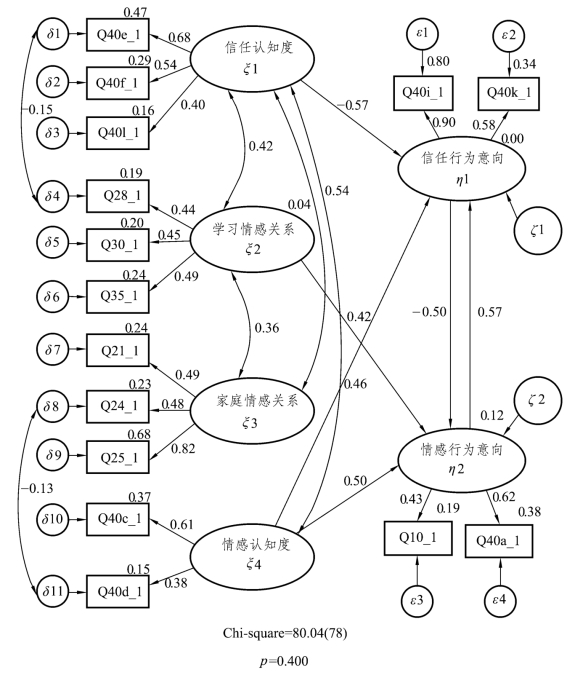
图5-8　修正的模型三

根据上面提出的如图5-8 所示的模型，在Amos 中运用极大似然估计运行的部分结果如表5-17 所示。

表5-16　常用拟合指数计算结果

从表5-16 可以看出，卡方值减小了很多，并且各拟合指数都得到了较大的改善。该模型的各个参数在0.01 的水平下都仍然是显著的，各方程对应的测定系数增大。经过修正之后的模型是合理的，是可用于分析的模型。表5-17 为各潜变量在外显指标上的负载和误差。

表5-17　各潜变量在外显指标上的负载和误差（N=384）

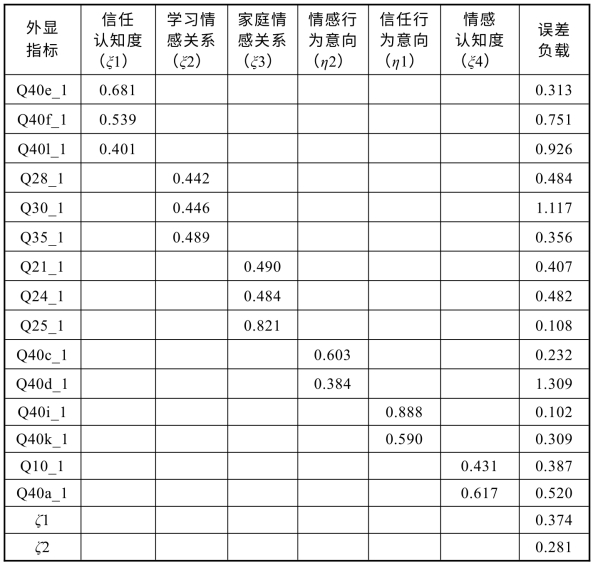
说明：Q40e_1——人与人之间应当相互信任；Q40f_1——人与人之间的信任是可以做到的；Q40l_1——信任别人会得到好的回报；Q40i_1——在家靠父母，出外靠朋友；Q40k_1——与人打交道还是谨慎点好；Q28_1——与同学关系；Q30_1——喜欢参加学校或班级开展活动；Q35_1——重视学习环境中的人际关系；Q21_1——家是最温暖的地方；Q24_1——与父亲的关系；Q25_1——与母亲的关系；Q10_1——对情感的态度；Q40a_1——人离不开爱情、亲情、友情这些情感的支持；Q40c_1——应当尊重情感生活的隐私性；Q40d_1——个人的情感是完全自由的