情感与信任关系的结构方程模型建构与验证成果

结构方程模型（Structural Equation Modeling，简称SEM）是一种非常通用的、主要的线性统计建模技术，被广泛应用于经济学、心理学、社会学、管理学等领域的研究中。在社会科学研究领域，有时需要处理多个原因、多个结果的关系，或者遇到不可直接观测的变量（潜变量），传统的统计方法对这些问题往往无能为力。而结构方程模型的发展，弥补了传统统计方法的不足，并迅速成为多元数据分析的重要工具。

所谓结构方程式模型旨在描述潜在自变量与潜在因变量之间的因果关系的模式，即界定潜在自变量与潜在因变量之间的线性关系。这种模式中的因和果通常是通过小型理论所假定或推定而来。潜变量分析方法的建模是以协方差矩阵为基础，使用最大似然估计法（maximum-likelihood estimation）得到参数估计值。主要按照假设的理论模型对所观测到的协方差矩阵进行计算，得到一个假设模型框架下的协方差矩阵，这两个协方差矩阵的吻合程度即为判定理论模型是否可接受的依据。二者都是用可观察到的外显变量来代替潜在变量。这种潜变量分析方法和多元回归相比，其优点表现为：首先，潜变量是由同一结构的多种任务共同组成的，每一个任务对结构内部相关估计的影响很小；其次，每一项任务的测量误差不包括在潜变量中，单项任务的测量误差和不可靠性对整体结果的影响比较小，从而单项任务的因素负荷具有较高的精确度。因此，潜变量分析法对设想结构的测量更加可靠、准确。

（一）结构方程模型架构

在 SEM 模式中，变量分为“潜在变量（latent variables）”与“观察变量（observed variables）”两大类。

1.潜在变量

潜在变量是一般行为，是社会科学中无法直接观察或测得的，必须由观察变量（observed variables）来间接推测得知。如本研究中的信任认知度（ξ1）、学习情感关系（ξ2）、家庭情感关系（ξ3）、情感认知度（ξ4）、信任行为意向（η1）与情感认知度（η2）。潜在变量又可分为以下两类：

（1）潜在自变量（latent Independent variable，ξ）：影响其他潜在变量的自变量，但潜在自变量之间不会彼此影响。如本研究中的信任认知度（ξ1）、学习情感关系（ξ2）、家庭情感关系（ξ3）、情感认知度（ξ4）。

（2）潜在因变量（latent dependent variable，η）：受到潜在自变量所影响的因变量，也可能受到其他潜在因变量的影响。如本研究中的信任行为意向（η1）与情感认知度（η2）。

2.观察变量

观察变量是可通过直接观测而得到的变量，大部分问卷中的测试题目均是观察变量。观察变量分为以下两类：

（1）X 变量：属于潜在自变量的观察指标；

（2）Y 变量：属于潜在因变量的观察指标。

潜在自变量与潜在因变量，都可经由观察变量来加以界定，在观察变量中，属于潜在自变量ξ的观察指标者称为X 变量，属于潜在因变量η的观察指标者称为Y 变量。这四种变量中，潜在自变量ξ与Y 变量没有直接关系，潜在因变量η与X 变量没有直接关系，η、ξ、X、Y 四种变量有下列五种关系（陈正昌、程炳林，1994）：

第一、潜在自变量ξ与潜在自变量ξ的关系，以Φ表示。

第二、潜在自变量ξ与潜在因变量η的关系，以Γ表示。

第三、潜在因变量η与潜在因变量η的关系，以β表示。

第四、潜在自变量ξ与X 变量的关系，以Λx 表示。

第五、潜在因变量η与Y 变量的关系，以ΛY 表示。

除上述五种关系外，SEM 模式另外包含以下三种误差关系：

第一，X 变量的测量误差，以δ表示。

第二，Y 变量的测量误差，以ε表示。

第三，潜在因变量η所无法被解释的残差，或称结构方程式的残余误差，以ζ表示。

前述的Φ、β、Γ、ΛX、ΛY、δ、ε、Ψ都是矩阵的形式，是SEM 的8 个参数矩阵，而由这8 个矩阵将再发展出最大似然估计式中的Σ与S 共变异矩阵。

（二）结构方程式模式（structural equation model）

结构模式方程式如下：

其中，ξ是潜在自变量，η是潜在因变量，Γ是潜在自变量对潜在因变量的影响效果的系数矩阵，β是潜在因变量对潜在因变量的影响效果的系数矩阵，ζ是残余误差。

（三）测量模式（measurement models）

测量模式是用来说明潜在变量与观察变量的关系，即界定潜在变量与观察变量之间的线性关系，故研究者实测的观察数据必须以直线关系作为切入点，才能被用来进行整个SEM 分析。我们假定受试者发生某些可观察的显性行为是由于某一项非观察潜在变量构成所导致的，潜在变量被假定是造成观察变量的因，但是潜在变量却不能直接观察到，必须由观察变量间接推论而得。下列SEM 测量模式即用来界定潜在变量与观察变量之间的关系的方程式：(www.xing528.com)

X 是观察自变量，ΛXξ是描述X 与ξ之关系的系数矩阵，δ是X 的测量误差。

Y 是观察因变量，ΛYη是描述Y 与η之关系的系数矩阵，ε是Y 的测量误差。从上面两条测量模式的直线中，我们可以知道如何利用观察变量来间接推测潜在变量。

结构方程式与测量方程式中的每一个元素都是矩阵，而且以上三个方程式也包含了前述SEM 模式的8 个参数矩阵。在进行SEM 分析时，研究者必须先根据理论画出因果模式路径图，并将所要估计的参数（parameters）代入结构公式及测量模式之中，然后估计共变异方程式所需的Φ、β、Γ、ΛX、ΛY、δ、ε、Ψ等8 个参数矩阵。

此8 个参数矩阵的估计必须由计算机以迭代（iteration）方式进行，每迭代一次，计算机程序自动将估计所得的8 个参数矩阵代入共变异矩阵中，并计算的适配函数（fitting function）值，随着迭代次数的增加，适配函数大致上越来越小。当前后两次的适配函数值差量小于收敛标准时，计算机就停止估计工作，此时所得的适配函数是为最小适配函数值。计算机并根据最小适配函数值进行χ2 检验。如果检定结果发现χ2 值不显著，则接受虚无假设，表示研究者所提出的理论模式与观察所得数据可以适配；反之，则表示研究者所提出的理论模式与观察所得数据就无法适配。

潜变量分析法能清晰地检测出哪一个模型和我们的数据最一致，好模型的获得需要变量的相关矩阵支持。简言之，假如许多观察变量归属于一个共同的潜变量，那么这些变量之间，至少应该存在中等程度的相关（反映了收敛效度）。如果相关低，它们就属于不同的潜变量（反映了区分效度）。假如用验证性因素分析能找到一个独特的模型来很好地拟合数据，那么这就意味着，模型假设的结构充分反映了收敛和区分效度。

潜变量分析法使用未标准化和标准化的形式提供了参数估计值，参数估计值与回归权重值类同。如果不做选择，输出结果默认的路径系数（或载荷系数）没有经过标准化，称作非标准化系数。非标准化系数中存在依赖于有关变量的尺度单位，所以在比较路径系数（或载荷系数）时无法直接使用，因此需要进行标准化。标准化权重估计，和回归分析一样是通过将所有的测量转换成相同的尺度来进行。标准化系数是将各变量原始分数转换为Z 分数^[1]后得到的估计结果，用以度量变量间的相对变化水平。因此不同变量间的标准化路径系数（或标准化载荷系数）可以直接比较。而且标准化路径系数值越大，该潜变量的影响程度越大。故本研究只报告完全标准化估计值。

（四）模型评价

一般而言，模型拟合优劣的评价包含两部分：模型的内在结构和整体拟合度。

1.模型内在结构的评价

评价模式的内在结构，主要是检验“违犯估计”，就是估计系数是否超出可接受范围。许多学者对检验的项目有不同的界定，但是文献中引用较多的是Hair 等（1998）的界定。他提出“违犯估计”的项目应该包括：（1）误差值存在负数；（2）标准误太大；（3）标准化系数超过或者接近1（通常以0.95 为门槛）。另外，评价各个具体的参数估计值是否达到显著水平，需要用t 检验。具体的参数估计值主要包含以下三部分：在结构方程模型图中，一般从潜变量指向观察变量比较长的单向箭头旁的数值表示因素负荷（也叫路径系数），是使用最大似然估计法得到的标准化回归系数，它表明潜变量对观察变量的影响程度；直接指向观察变量的、比较短的单向箭头旁的数值表示测量误差，是指每一项测量任务中那些没有被潜变量解释的变异；从潜变量指向潜变量的双向箭头旁的数值表示潜变量之间的相关系数。这三部分的参数估计值，在没有额外说明的情况下表示都是显著的。详细的检验标准是：各个参数估计值的t 值的绝对值大于1.96 时，表明估计参数已经达到0.05 的显著水平；t 值的绝对值大于2.58 时，表明估计参数已经达到0.01 的显著水平（黄芳铭，2005：238 ）。可见，模型中有效的参数估计值，其t 值至少应该大于1.96。

2.模型整体拟合度的评价

当模型的内在结构良好时，下一步需要评价模型的整体拟合优劣。评价整体拟合优劣要解决两个问题：第一，应当根据哪些指数来检验模型？因为指数是反映理论模型与样本数据吻合程度的统计量；第二，多大的指数值才算是一个“好”的模型？这里的指数值类似于通常的假设检验中统计量的临界值（cutoff value）。实际上，这两个问题都是结构方程分析中很重要、且尚未很好解决的问题（温仲麟、侯杰泰、马什赫伯特，2004）。从1973 年第一个指数TLI 产生至1996 年NTFI 的提出，文献上正式发表的指数已有40 多个（温仲麟、侯杰泰、马什赫伯特，2004）。那么，选择哪些指数最能有效地评鉴模型？依据Hoyle、Panter 以及侯杰泰等人（2004）的建议，评价模型整体拟合度的指数，应该包含以下这些：

（1）卡方（χ2 ，Minimum Fit Function Chi-Square）

（2）自由度（df，degrees of freedom）

（3）比较吻合度指数（CFI，comparative fit index）

（4）非范拟合指数（NNFI，Non-Normed Fit Index，也称为TLI）

（5）近似误差均方根（RMSEA，Root Mean Square Error of Approximation）

首先，卡方值是一种常用的拟合统计指标，它不仅本身是一个重要的指数，而且大多数指数都是它的函数。卡方值测量的是模型再生的相关矩阵与观察变量的原始相关矩阵之间的差异程度：卡方值越小，表明二者的差异越不显著，也就是说模型拟合比较理想。值得注意的是，潜变量分析法中卡方的显著性检验的临界值与N（样本量）和自由度都有关，而传统的卡方检验临界值只与自由度有关，与N 无关。可见，这里的卡方只是近似服从传统的χ2 分布，所以要突破传统χ2 检验的临界值0.05 或0.01。于是实际研究中，当N 大于250 时，其显著性水平应该为0.0005；当N 大于500 时还可以更小（温仲麟、侯杰泰、马什赫伯特，2004）。但是，卡方检验随样本大小的变化比较大。当样本增大时，即使模型再生的相关矩阵与观察变量的原始相关矩阵之间差异非常小，卡方值也会显著增大。于是，Joreskog 在1970 提出一个新的模型拟合度评价指标“Normed chi-square”，它将卡方检验和自由度结合起来，即χ2 /df。并有人建议，当χ2 /df 在1.0和2.0 或者3.0 或者5.0（更宽松的情况下）之间时模型拟合可以接受（Hai，等，1998）。但是，侯杰泰等（2004：156）和Hollen 等（1993）认为，χ2 /df同样易受样本容量的影响，对于评价单个模型的意义不大。所以，卡方值和自由度对于鉴别模型的意义不太大，二者的主要功能在于模型比较（侯杰泰，等，2004：45，120-121）。而且许多研究并不报告卡方检验的显著性（即p 值）。可见，对几个可接受模型的拟合优劣程度作精确比较时，才需要用到卡方值和自由度。具体操作方法是用两个模型的卡方之差作为新的卡方，两个模型的自由度之差作为新的自由度，如果卡方检验不显著，则新增的参数是多余的。

其次，比较吻合度指数（CFI）相当于将RNI 在0～1 之外的值进行截取，使其取值范围变成了0～1。而非范拟合指数（NNFI，也叫TLI）是一种非规范性指标，所以它产生的值可能会超出0 到1 之间。很长一段时间内比较公认的标准是，相对指数CFI 和NNFI 的值在0.9 或以上，表示拟合模型可以接受（例如，侯杰泰、温仲麟、成子娟，2004：45）。而且，很多研究者推荐使用这两个指标（例如，温仲麟、侯杰泰、马什赫伯特，2004）。

最后，近似误差均方根（RMSEA）是近年来相当受重视的一个模式适配指标，几乎所有的结构方程建模文献中都使用它。而且很多研究显示，它在评价鉴别模型拟合度时，比其他指标更好。Steiger（1990）提出，RMSEA的值低于0.10 表示模型拟合好；低于0.05 表示拟合非常好；低于0.01 表示拟合非常出色，不过这种情形几乎碰不到。后来又有人对上述标准做了一些补充：RMSEA 值介于0.05 到0.08 之间，可以视为“算是不错的适配”；介于0.08 到0.10 之间则是“中度适配”，可以接受（黄芳铭，2005：151）。通常，文献中的研究都将RMSEA 值等于小于0.08 定为是“良好适配”，表示假设的模型基本可以接受；小于0.05 定为是“很好适配”，表示假设的模型完全可以接受。

表4-1　拟合指数对比表

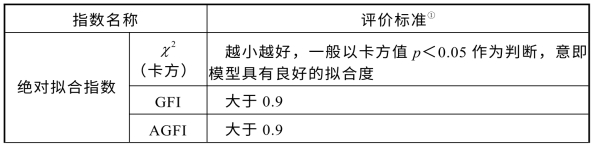
①表格中给出的是该拟合指数的最优标准，譬如对于RMSEA，其值小于0.05表示模型拟合较好，在0.05～0.08 间表示模型拟合尚可（Browne&Cudeck，1993）。因此在实际研究中，可根据具体情况分析。

续表

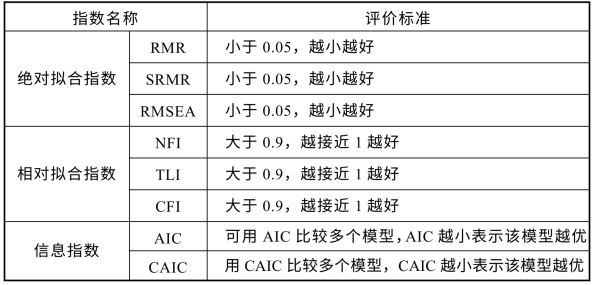
研究报告中出现频率较高的其他指数还有如下一些：NFI、GFI 和AGFI也是许多学者建议列出的指数，这三个指标的可接受模型的共同推荐值一般都是0.9（含）以上（越大越好）（黄芳铭，2005：149-155）。所以，本研究在随后的建模过程中报告那些出现频率较高的指数（见表4-1），如：χ2、df、p 值，CFI、TLI、NFI、GFI 和AGFI 也一并列出。

需要注意的是，拟合指数的作用是考察理论模型与数据的适配程度，并不能作为判断模型是否成立的唯一依据。拟合优度高的模型只能作为参考，还需要根据所研究问题的背景知识进行模型合理性讨论。即便拟合指数没有达到最优，但一个能够使用相关理论解释的模型更具有研究意义。