王工一
怎样教学数学中的难题？进行循序渐进的训练是一种行之有效的方法。第24届国际奥林匹克数学竞赛试题的第六题（数论问题），当时的全体主试委员没有一个能够解出，后来将这道题交给澳大利亚四位最好的数论专家，每人花了一整天时间仍然没有解决。由此可见该题的难度之大。但是万丈高楼平地起，通过循序渐进的系统训练，这些难题仍是可以突破的。参加第24届国际奥林匹克数学竞赛的选手就有11名解出了这道数学难题。
我在辅导小学生参加数学竞赛时，曾碰到过这样一道题目：
如图1，8个同样大小的圆，其中7个固定不动，第8个（有阴影的）紧贴这7个圆无滑动地滚动。试问当它沿着7个定圆滚回出发点时，本身转了多少个圈？
这道题目应该说有一定难度，但如果对学生进行以下几道题目的训练，再回过头来解这道题就会显得得心应手。
（1）如图2，当圆沿直线从A无滑动地滚到B时（AB的长度与圆周长相等），求圆滚动的圈数。
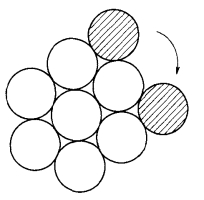
图1
图2
显然圆刚好滚动了一圈。由此还可推得，当AB的长度不等于圆周长时，圆从A无滑动地滚动到B时，所滚动的圈数=AB的长度÷圆周长。
（2）如图3，一个圆在等边三角形的外侧与等边三角形的边相切滚动，且不发生滑动。如果等边三角形的一边长等于这个圆的周长，那么当圆沿着三角形的边滚回出发点时，圆本身转了几个整圈？
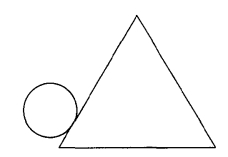
图3(www.xing528.com)
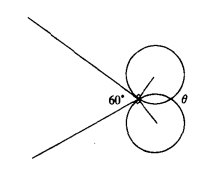
图4
分析：圆沿着三角形作直线上滚动，其转动的圈数是三角形的周长除以圆周长来计算（共转了3圈）；圆在三角形每个顶点上转动时，圆有一个由与一边相切转到与另一边相切的过程（如图4），在这个过程中，圆上的一点始终没有离开三角形的这个顶点，但它在这个过程中本身在转动，由图4可知，转动的角度是：
θ=180°-60°=120°
所以经过3个顶点共转了120°×3=360°，即1圈，故该题的答案是4圈。
从这道题目可以得到一个启示：圆在直线上滚动和在曲线上滚动是不一样的。
（3）圆在与它同样大小的圆上作无滑动滚动，如图5，中间圆表示定圆，两边的圆表示动圆，从定圆的一侧滚动到另一侧，问：动圆滚了几圈？
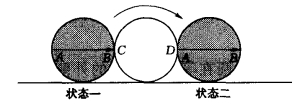
图5
分析：观察动圆直径的两端点A、B，动圆上的B点原先与定圆的C点相切，当动圆从状态一滚到状态二时，动圆的A点转到定圆的D点，并与之相切，从图上可以明显看出BA刚好转了一圈，即圆滚动了一圈，而圆滚动的距离为CD——半个圆周。由此可以得到启示：圆在和它半径相同的定圆的圆弧上滚动，它滚动的角度等于它滚过的圆弧所对的圆心角的两倍。
图6
有了这些准备，我们就可以解上面这道题目了。解：从图6中可以看到动圆在一个定圆上滚动的弧所对的圆心角为120°，即
圈，这样，动圆在这个过程中转了：
（圈）。滚回出发点，即滚了6个圆，所以本身转了
（圈）。
【本文原刊于《中小学数学》2000（1-2）】
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
