实用数学：组合数公式

从n个不同元素中取出m（m≤n）个元素的所有组合的个数，叫做从n个不同元素中取出m个元素的组合数，用符号表示（C是组合的英文Combination的第1个字母）.

例如，从1，2这两个元素中，每次任意取出1个作为1个组合，那么它可以构成两个组合，即＝2，这个结果2是从2个元素中任取1个元素的不同组合的个数，即组合数.

从9个不同元素中，取出4个元素的组合数表示为；从6个不同元素中取出3个元素的组合数表示为.

很显然，排列问题与组合问题有着密不可分的关系，本节将从研究组合数与排列数的关系入手，找出组合数的计算公式.

例如，从4个不同元素a，b，c，d中取出3个元素的排列与组合的关系如下表4-3所示：

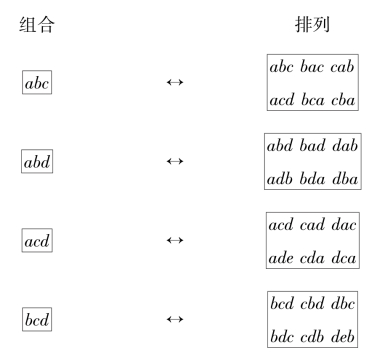
图4-3

由表中可以看出，对于相应的每一个组合，都有个不同的排列.因此，求从4个不同元素中取3个元素的排列数，可以按照下面的考虑方法分两步完成：

第1步　从4个不同元素中取出3个元素做组合，共有个，由上表可知＝4；

第2步　对每一组合中的3个不同元素做全排列每一组合对应的全排列都是＝6个.

根据分步计数原理，得：

类比可得：

因此

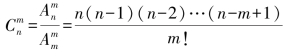
这里n，m是正整数，并且m≤n.这个公式叫做组合数公式.

例1　计算及.

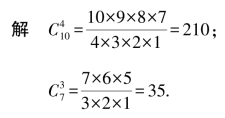(https://www.xing528.com)

例2　从10名运动员中，选出3名参加比赛，问有多少种选法？

解　实际上这是从10个不同元素中取出3个元素的组合问题，即：

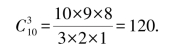
也就是说，有120种选派方法.

例3　平面内有12个点，其中任意3点都不在同一条直线上，以任意3点为顶点画三角形，一共可画多少个三角形？

解　因为平面内的12个点中任意3点都不在同一直线上，所以，任意3个点都可以构成一个三角形的顶点，那么以平面内12点的任意3个点画三角形，可以画出的三角形个数，就是从12个不同元素中取出3个元素的组合数，即：

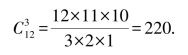
排列问题与组合问题的根本区别在于，取出元素后是否要按一定顺序排列.元素需要按一定顺序排列，属排列问题；不需要考虑元素顺序，属组合问题.

例4　（1）从全班50人中选班委7人，共有多少种不同的选法？

（2）从全班50人中选班长、副班长、学习委员体育委员、宣传委员、生活委员、文娱委员各一人，共有多少种不同的选法？

解　（1）＝99884400；

（2）＝50×49×48×47×46×45×44＝503417376000.

练习

1.指出排列与组合的区别是什么？并各举一个例子.

2.计算：.

3.平面内4点中，任意3点不共线，那么它们可连成多少条线段？

4.写出从a，b，c，d，e这5个元素中取出2个和3个元素的所有组合.

5.从1，2，3，4，5，6，7，8，9这9个数中取出两个数，使它们的和是偶数，共有多少种取法？