初中概率：随机事件频率规律性探究

在初中阶段，我们已经了解了必然事件、不可能事件和随机事件等概率论中的一些基本概念.

生活中有很多随机事件的例子，如“明天本地下雨”“买一张彩票中奖”等，随机事件在一次试验中是否发生具有不确定性，但是在相同条件下的大量重复试验中，它发生的频率是否会呈现出一定的规律性呢？

历史上曾有人做过掷硬币的试验，试验结果如表4-1.

表4-1

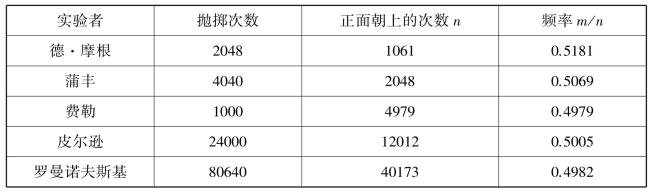
重复抛掷硬币，出现“正面朝上”的频率是事先无法确定的但是在大量重复抛掷硬币时，出现“正面朝上”的频率具有稳定性，它在0.5附近摆动.

抽象概括

在相同的条件下，大量重复进行同一试验时，随机事件A发生的频率会在某个常数附近摆动，即随机事件A发生的频率具有稳定性.这时，我们把这个常数叫作随机事件A的概率，记作P（A），我们有0≤P（A）≤1.

频率反映了一个随机事件出现的频繁程度，但频率是随机的，而概率是一个确定的值，因此，人们用概率来反映随机事件发生的可能性的大小，我们常常通过做大量的重复试验，用随机事件发生的频率作为它的概率的估计值，但是重复大量试验，操作起来不方便，有更简便的方法求随机事件发生的概率吗？

例1　抛掷一枚硬币，假设硬币的构造是均匀的，并且掷得的结果只可能是“正面向上”或“反面向上”问掷得“正面向上”的可能性有多大？

解　由于硬币的构造是均匀的，因而出现“正面向上”与“反面向上”的机会是均等的，又排除了其他可能，所以我们可以断定，抛掷一枚硬币，掷得“正面向上”和“反面向上”的可能性都是.

例2　抛掷一颗骰子，设骰子的构造是均匀的，问掷得的可能结果有哪些？掷得6点的可能性有多大？

解　抛掷一颗骰子，只可能出现以下6种结果之一：“掷得1点”“掷得2点”“掷得3点”“掷得4点”“掷得5点”和“掷得6点”.由于骰子的构造是均匀的，因而出现这6种结果的机会是均等的，于是我们可以断定：抛掷一颗骰子，“掷得6点”的可能性是.

例3　连续抛掷两枚均匀的硬币，问可能出现的结果有哪些？两枚都出现正面向上的可能性有多大？

解　我们分别用“正”表示“正面向上”，“反”表示“反面向上”，那么连续抛掷两枚硬币可能出现的所有结果组成的集合是：

Ω＝｛（正，正），（正，反），〈反，正），（反，反）｝

其中（正，正）表示两枚都正面向上，（正，反）表示第一枚正面向上；第二枚反面向上；（反，正）表示第一枚反面向上；第二枚正面向上，（反，反）则表示两枚都反面向上.

因为每一枚硬币“出现正面”与“出现反面”机会是均等的，所以这四种结果的出现是等可能的.因而我们说两枚硬币均出现“正面向上”的可能性是.

通常把对某种现象的一次观察、测量或进行一次科学实验，统称为一个试验.如果这个试验在相同的条件下可以重复进行，且每次试验的结果事先不可预知，则称此试验为随机试验，也简称为试验.

在随机试验中，如果其可能出现的结果有限个，且它们出现的机会是均等的，我们称这样的随机试验为古典概型.容易看出上述三个例子均属古典概型.

我们把一个随机试验的一切可能结果构成的集合叫做这个试验的样本空间，常用大写希腊字母Ω表示.

显然，古典概型的样本空间是有限集.

例1中的样本空间

Ω＝｛正，反｝，

例2中的样本空间

Ω＝｛1，2，3，4，5，6｝，

其中1，2，3，4，5，6表示掷得的点数.

例3中的样本空间

Ω＝｛（正，正），（正，反），（反，正），（反，反）｝.

在古典概型中，有时需要进一步研究一些问题.例如，在例2中我们还需求“掷得偶数点”的可能性；在例3中还需求“恰有一枚掷得正面”的可能性等.

我们知道，在例2中“掷得偶数点”是由“掷得2点”“掷得4点”和“掷得6点”这三种结果组成的，是样本空间的一个子集；在例3中“恰有一枚正面”是由（正，反）和（反，正）这两个结果组成的，也是例3的样本空间的一个子集，我们把样本空间的子集，叫做随机事件，简称事件.常用大写英文字母A，B，C等表示，只含有一个元素的事件通常叫做基本事件.

每一个事件由若干基本事件组成.例如，在例3中恰有一枚掷得正面”就是｛（正，反），（反，正）｝，例2中“掷得偶数点”就是｛2，4，6｝.

为了方便，我们把某一试验中不可能发生的事件（即空集）叫做不可能事件，在做某一试验时，必然发生的事件（即全集）叫做必然事件.

如在例2中“掷得7点”“掷得8点”，样本空间中没有这里所说的两个元素，它们都是空集，是不可能事件，而“掷得的点数不大于6”＝｛1，2，3，4，5，6｝＝Ω为这个试验的样本空间，一定是必然事件.

在例2中，“掷得偶数点”＝｛2，4，6｝，就是出现掷得2点”“掷得4点”“掷得6点”这三者之间一时发生，因而“掷得偶数点”的可能性应该是这三者可能性之和，即.

在例3中，“恰有一枚掷得正面”是由（正，反）和（反，正）这两个结果组成的.出现“恰有一枚掷得正面”就是出现上述结果之一，因为每一个结果出现的可能性为，所以“恰有一枚掷得正面”的可能性为.

一般地，对于古典概型，如果试验的基本事件总数为n，随机事件A所包含的基本事件数为m，我们就用来描述事件A出现的可能性大小，称它为事件A的概率，记作P（A），即：

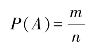
显然事件A的概率满足

0≤P（A）≤1

而且，必然事件的概率是1，不可能事件的概率是0，即：

P（Ω）＝1，P（ϕ）＝0.

可以用古典概型计算的概率叫做古典概率.

例4　从含有两件正品a1，a2和一件次品b1的三件产品中每次任取一件，每次取出后不放回，连续取两次，求取出的两件中恰好有一件次品的概率.(https://www.xing528.com)

解　每次取后不放回地连续取两次，其一切可能的结果组成的样本空间为

Ω＝｛（a1，a2），（a1，b2），（a2，b1）｝

（其中括号内的字母表示取出的产品，不考虑顺序）

Ω由3个基本事件组成，由于每一件产品被取到的机会是均等的，因此这些基本事件的出现是等可能的.用A表示“取出的两件中，恰好有一件次品”这一事件，则：

A＝｛（a1，b2），（a2，b1）｝

事件A由2个基本事件组成.因而：

例5　在例4中，把“每次取出后不放回”这条件换成“每次取出后放回”，其余不变，求取出的两件中恰好有一件次品的概率.

解　有放回地连续两次取得的两件，其一切可能的结果组成的样本空间.

Ω＝｛（a1，a1），（a1，a2），（a1，b1），（a2，a1），（a2，a2），（a2，b1），（b1，a1），（b1，a2），（b1，b1）｝

由9个基本事件组成.由于每一件产品被取到的机会均等，因此这些基本事件的出现是等可能的.用B表示“恰有一件次品”这一事件，则：

B＝｛（a1，b1）（a2，b1），（b1，a1），（b1，a2）｝

事件B由4个基本事件组成，因而：

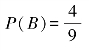
例6　抛掷两颗骰子，求：

（1）出现点数之和为7的概率；

（2）出现两个4点的概率；

解　如下表：抛掷两颗骰子，其一切可能的结果组成的样本空间Ω＝｛（1，1），（1，2），（1，3），（1，4），（1，5），（1，6）…（6，1），（6，2）（6，3），（6，4），（6，5）（6，6）｝，Ω有36个基本事件组成

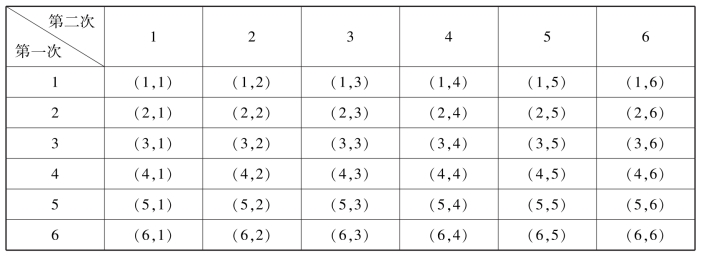
（1）记“出现点数之和为7”的事件为A，可看到事件A包含的基本事件共6个，为

（6，1），（5，2），（4，3），（3，4），（2，5），（1，6）

所以：

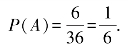
（2）记“出现两个4点”的事件为B，则可看到事件B包含的基本事件只有1个，为（4，4）.

所以：

复习题

1.从含有两件正品和一件次品的三件产品中任取两件，求取出的两件中恰有一件次品的概率，并与例4比较异同.

2.从1，2，3，4，5中，任取两个数，求两个数都是奇数的概率.

3.在40根纤维中，有12根的长度超过30mm.从中任取1根，取到长度超过30mm的纤维的概率是多少？

4.在10支铅笔中，有8支正品和2支次品.从中任取2支，恰好都取到正品的概率是多少？

5.同时抛掷2分和5分的两枚硬币，计算：

（1）两枚都出现正面的概率；

（2）一枚出现正面，一枚出现反面的概率.

6.甲同学在求事件A的概率时，算得事件A的概率P（A）＝1.2，乙知道后说“你一定算错了”.试问乙的根据是什么？

7.抛掷两颗骰子，计算：

（1）事件“两颗骰子点数相同”的概率；

（2）事件“点数之和小于7”的概率；

（3）事件“点数之和等于或大于11”的概率；

（4）在点数和里最容易出现的数是几？

8.某射手在同一条件下进行了射击，结果如下表所示：

（1）计算表中击中靶心的各个频率；

（2）这名射手射击一次，击中靶心的概率约是多少？