实用数学：3个班选1名好学生的分类计数原理

问题1　从甲地去乙地，可以乘火车，也可以乘汽车，一天中，火车有2班，汽车有4班，那么一天中乘坐这些交通工具从甲地到乙地有多少种不同的选择？

在一天中，从甲地到乙地乘火车有2种选择，乘汽车有4种选择，以上每一种选择，都可以从甲地到达乙地.因此，一天当中乘坐这些交通工具从甲地到乙地的不同选择共有：

2＋4＝6（种）

一般地，有如下原理：

分类计数原理　完成一件事，有n类办法，在第1类办法中有m1种不同的方法，在第2类办法中有m2种不同的方法……在第n类办法中有mn种不同的方法，那么完成这件事共有：N＝m1＋m2＋…＋mn种不同的方法.

例1　书架上层有不同的数学书15本，中层有不同的语文书18本，下层有不同的物理书7本.现从其中任取一本书，问有多少种不同的取法？

解　从书架上任取一本书，有三类取法：

第1类取法是从书架的上层取出一本数学书，可以从15本中任取一本，有15种取法；

第2类取法是从书架的中层取出一本语文书，可以从18本中任取一本，有18种取法；

第3类取法是从书架的下层取出一本物理书，可以从7本中任取一本，有7种取法.

只要在书架上任意取出一本书，任务即完成，根据分类计数原理，不同的取法一共有：

N＝m1＋m2＋m3＝15＋18＋7＝40（种）

例2　某班同学分成甲、乙、丙、丁四个小组，甲组9人，乙组11人，丙组10人，丁组9人，现要求该班选派一人去参加某项活动，问有多少种不同的选法？

解　该班同学分成甲、乙、丙、丁四个小组，从任何一个小组中选出一名同学去参加活动，则任务完成甲组有9种选法，乙组有11种选法，丙组有10种选法，丁组有9种选法，所以一共有：N＝9＋11＋10＋9＝39种选法.

问题2　由A地去C地，中间必须经过B地，且已知由A地到B地有3条路可走，再由B地到C地有2条路可走（图4-1），那么由A地经B地到C地有多少种不同的走法？

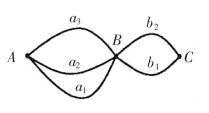
图4-1

这里，从A地到C地不能由一个步骤直接到达，必须经过B地，从A地到B地有3种不同的走法，分别用a1，a2，a3表示，而从B地到C地有2种不同的走法，分别用b1，b2表示，所以从A地经B地到C地的全部走法有：

a1b1，a1b2，a2b1，a2b2，a3b1，a3b2

共计6种.就是从A地到B地的走法数3与从B地到C地的走法数2的乘积，即

3×2＝6（种）.

一般地，有如下原理：

分步计数原理　完成一件事，需要分成n个步骤，做第1步有m1种不同的方法，做第2步有m2种不同的方法……做第n步有mn种不同的方法，那么完成这件事共有：N＝m1×m2…×mn种不同的方法.

例3　书架上层有不同的数学书15本，中层有不同的语文书18本，下层有不同的物理书7本，现从中取出数学、语文、物理书各一本，问有多少种不同的取法？

解　从书架上取数学、语文、物理书各一本，可以分成三个步骤完成：

第1步，取数学书一本，有15种不同的取法；

第2步，取语文书一本，有18种不同的取法；

第3步，取物理书一本，有7种不同的取法；

符合分步计数原理的条件，利用分步计数原理，得到：N＝15×18×7＝1890种不同的取法.

例4　某农场要在4种不同类型的土地上，试验种植A、B、C、D这4种不同品种的小麦，要求每种土地上试种一种小麦，问有多少种不同的试验方案？

解　第1步，先考虑A种小麦，可在4种不同类型的土地中任选1种，有4种选法；

第2步，考虑B种小麦，可在剩下的3种不同类型的土地中任选1种，有3种选法；

第3步，考虑C种小麦，再在剩下的2种不同类型的土地中任选1种，有2种选法；(www.xing528.com)

第4步，最后考虑D种小麦，只剩下1种类型的土地，因此只有1种选法.

以上4步依次完成，才算完成，依据分步计数原理，可知有：4×3×2×1＝24种不同的试验方案.

例5　由数字1，2，3，4，5可以组成多少个三位数？（个位上的数字可以重复）

解　用1，2，3，4，5这5个数字组成三位数可以分成三个步骤完成：

第1步，确定百位上的数字，从上面5个数字中任取1个数字，共有5种取法；

第2步，确定十位上的数字，因为数字可以重复，所以仍有5种取法；

第3步，确定个位上的数字，同理，亦有5种取法.

根据分步计数原理，组成不同的三位数的个数共有：5×5×5＝125（个）

上述两个基本原理的共同点是，都是研究“完成一件事，共有多少种不同的方法”，它们的区别在于一个与“分类”有关，一个与“分步”有关.

如果完成一件事有n类不同的办法，无论哪一类办法中的哪一种都能单独地完成这件事，求完成这件事的方法的总数，就用分类计数原理；如果完成一件事，需要分成n个步骤，各个步骤都不可缺少，需要完成所有的步骤才能完成这件事，而完成每一个步骤又各有若干方法，求完成这件事方法的种数，就用分步计数原理.

例6　甲班有三好学生8人，乙班有三好学生6人，丙班有三好学生9人：

（1）由这3个班中任选1名三好学生，出席三好学生表彰会，有多少种不同的选法？

（2）由这3个班中各选1名三好学生，出席三好学生表彰会，有多少种不同的选法？

分析：（1）可以这样想：要完成由3个班中任选1名三好学生这件事，有几种选法？

当由甲班产生1名时，有多少种不同的选法？

当由乙班产生1名时，有多少种不同的选法？

当由丙班产生1名时，有多少种不同的选法？

由于这3种办法都能完成“由3个班中任选1名好学生”这一件事，故符合分类计数原理.

（2）可以这样想：要完成由3个班中各选1名三好学生这件事要分哪几步？各步分别有几种不同的选法？由于这几步中的任何一步，都不能单独完成“由3个班中各选1名三好学生”这件事，所以不符合分类计数原理，但当依次完成这3步时，就能完成这件事，故符合分步计数原理.

解　（1）依分类计数原理，不同的选法种数是：

N＝m1＋m2＋m3＝8＋6＋9＝23；

（2）依分步计数原理，不同的选法种数是：

N＝m1·m2·m3＝8×6×9＝432.

即由3个班中任选1名三好学生，有23种不同的选法；由3个班班中各选1名三好学生，有432种不同的选法.

练习

1.一件工作可以用两种方法完成，有5人会用第1种方法，另外有4人会用第2种方法完成，要选出1个人来完成这件工作，共有多少种方法？

2.一个学生要从2本科技书、2本政治书、3本文艺书中任取1本，共有多少种不同的取法？

3.4张卡片的正反面分别有0与1，2与3，4与5，6与7，将其中2张卡片排放在一起，可组成多少个不同的两位数？

4.从A地到B地有2条路可通，从B地到C地有3条路可通，从A地到D地有4条路可通，从D地到C地有2条路可通，从A地到C地共有多少种不同的走法？

5.一个口袋内有5个小球，另一个口袋内有4个小球，所有这些小球的颜色互不相同：

（1）从两个口袋内任取1个小球，有多少种不同的取法？

（2）从两个口袋内各取1个小球，有多少种不同的取法？