实用数学下册-位移与向量的表示

在物理学和其他的一些学科中，经常遇到的一些量，如距离、时间、面积、质量等，在选定度量单位后，就可用一个实数确切地表示它们，这种只有大小的量叫做数量（也称为标量）.另外一些量，它们不但有大小，而且还有方向.

位移就是一个既有大小又有方向的量.

我们把位移这一类具有大小和方向的量叫做向量（也称为矢量）.

问题1　如何描述平面上一点的位移？

假设一个质点从始点A移动到终点B，显然，最直观的方法，是用线段AB，并在终点B处画上箭头表示A到B的方向，来描述这个位移

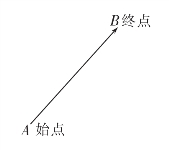
图2-1

上述标有方向的线段，叫做有向线段.

这就是说，平面内任意一点的位移，都可以转化为用一条有向线段来表示.

以A为始点，以B为终点的有向线段，记作AB应注意，始点一定要写在终点的前面.

位移，在物理学中只表示质点位置的变化，而与质点实际运动的始点和路线无关.在图2-2中，点A′相对于点A的位移，点B′相对于点B的位移，点C′相对于点C的位移，都是同一个位移或相等的位移；北偏东45°，3个单位.

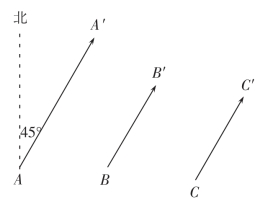
图2-2

印刷时，向量常用黑体小写英文字母a、b、c表示，手写时，用带箭头的小写英文字母表示.

向量的例子是很多的.例如，位移、力，速度等都是向量.有些向量不仅有大小和方向，而且还有作用点.例如，力就是既有大小、方向，又有作用点的向量.有些向量只有大小和方向，而无特定的位置.例如，位移、速度等就是只有大小和方向的向量，通常把后一类向量叫做自由向量.在本章学习的主要是自由向量，以后我们说到向量，如不特别说明，指的都是自由向量.这就是说，本章所学的向量只有大小、方向两个要素.如果两个向量的大小相同，方向相同，则说这两个向量相等.

由于我们所研究的向量只含有大小和方向两个要素，用有向线段表示向量时，与它的始点的位置无关，即：

同向且等长的有向线段表示同一向量，或相等的向量：

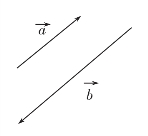
图2-3

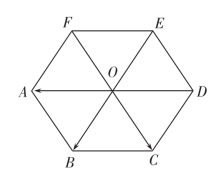
例：如图2-4所示，设O是正六边形ABCDEF的中心，分别写出与相等的向量.

(www.xing528.com)

图2-4

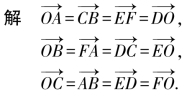
问题2：如何用向量确定平面内一点的位置呢？

任给一定点O和向量（图2-5），过点O作有向线

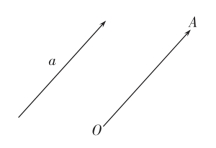
图2-5

则点A相对于点O的位置被向量所唯一确定.这时向北京量通常叫做点A相对于点O的位置向量.

例如，在谈到天津相对于北京的位置时，我们说，“天津位于北京东偏南50°，114km”.如图2-6，点O表示北京的位置，点A表示天津的位置，那么向量＝“东偏南50°，114km”就是天津相对于北京的位置向量.

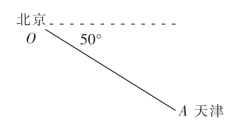
图2-6

有了位置向量的概念，我们就可以利用位置向量来确定一点相对于另一点的位置，这样，我们就可以用向量来研究几何了.

练习

1.选择适当的比例尺，用有向线段表示下列位移：

（1）飞机向南飞行50km；（2）飞机向西飞行50km；

试问以上两个位移的长度是否相等？两个位移是否相等？

2.在平面上任意确定一点O，点P在点O“东偏北60°，3cm”处，点Q在点O“南偏西30°，3cm”处，画出点P和点Q相对于点O的位置向量.

3.已知D，E，F是△ABC三边AB，BC，CA的中点，分别写出图中与相等的向量.

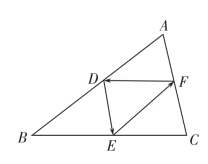
（第3题）

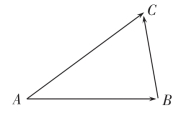
图2-7