实用数学：任意角三角函数

在初中，我们学过直角三角形中锐角的正弦、余弦、正切的值，这都是锐角的三角函数，锐角的正弦，余弦和正切函数，统称为锐角三角函数.

【问题1】当我们把锐角的概念推广为转角后，我们如何定义任意角的三角函数呢？

【定义】设角α终边上一点P（x，y）r＝｜op｜＝

我们把：叫做角α的余弦，记作cosα，即：cosα＝

叫做角α的正弦，记作sinα，即：sinα＝

叫做角α的正切，记作tanα，即：tanα＝

对于每一个确定的角α，都分别有唯一确定的余弦值，正弦值，正切值与之对应，所以这三个对应关系都是以α为自变量的函数，分别叫做角α的余弦函数，正弦函数和正切函数.

【问题2】任给一个角，我们如何求出它的三角函数值呢？

根据正弦、余弦和正切函数的定义，可得到计算三角函数值的步骤；

S1　在直角坐标系xoy中，作转角等于α；

S2　在α终边上任找一点P，找出该点的横坐标和纵坐标；

S3　根据三角函数的定义，求该三角函数的值.

例1　已知角α终边上一点P（2，-3），求角α的三个三角函数的值（如图）

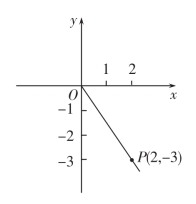
例1

解　已知P（2，3）则

由三角函数的定义，得：

例2　试确定三角函数在各象限的符号.(www.xing528.com)

解　由三角函数的定义可知，角α终边上一点的纵坐标，y与横坐标x的正、负分别与α的正弦函数值和余弦函数值同号.tanx＝，当x与y同号时，它们的比值为正，当x与y为异号时，它们的比值为负，即当α为第三象限的角时，tanα＞0，当α为二、四象限角时，tanα＜0，以上结果如图

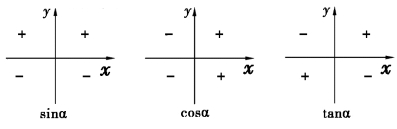
例2

［定义］如图1-5，在直角坐标系xOy中作以O为圆心，以1为半径的单位圆与角α终边交于点P、与x轴正半轴交于A、过P作x轴的垂线交x轴于点M，过A作圆的切线交α角的终边或其反向延长线于（T），则

∵｜OP｜＝1，

∴　点P的坐标x，y分别为cosα，sixα，即p（cosα，sixα）.

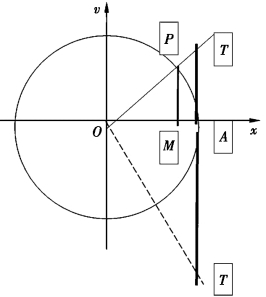
图1-5

∴　cosα＝x＝OM

sixα＝y＝MP

我们把规定了方向的线段OM，MP分别称做α的余弦线和正弦线.

我们把规定了方向的线段（AT）叫做α的正切.

练习

1.已知点P在角α的终边上，求角α的三个三角函数值：

（1）P（3，1）；（2）（2，2）；（3）P（2，2）；（4）P（-1，3）；（5）P（-3，3）；

（6）P（-3，3）；（7）P（-3，-1）；（8）P（1，-1）.

2.在直角坐标系的单位圆中，分别画出120°的30°的正弦线，余弦线和正切线.

3.已知角α终边上一点P（0，1），求角α的正弦函数值和余弦函数值.

4.已知角α终边上一点P（3，0），求角α的正弦函数值和余弦函数值.