个体弱序偏好中的知识水平分析

考虑建立在对象集合X＝｛x1，x2，…，xm｝上的弱序关系，xi≻xj表示xi优于xj，xi～xj表示xi和xj无差异即形成平局［92］。

假设人们用基于弱序的、允许包含平局的偏好序来表示偏好。由前面第5章知道，允许包含平局的偏好序与偏好映射是一一对应的，偏好映射的分量是集合，其中的元素表示对象可能的排序位置。由第5章，一个偏好映射PM＝（PMi）m×1，按照式（7.13）定义

其中ξi＝∈X，xj≻xi｝为对象xi的优先集，ηi＝∈X，xj～xi｝为对象xi的无差异集。

比如，假设对象集为X＝｛x1，x2，x3，x4｝，并假设一个建立在弱序关系基础上的偏好序为x1≻x2～x3≻x4，则该偏好序对应的偏好映射为

需要强调的是，法规允许下的偏好本身没有好坏之分。因此度量偏好之中的知识也不应该基于序的先后，而应该基于对对象的区分程度。由第5章知道（性质5.1），偏好映射的不同分量构成了集合I＝｛1，2，…，m｝上的有序划分，这是因为偏好映射的分量是由无差异关系（即等价关系）推出来的［式（7.13）］。因此，偏好映射之中包含的用于区分的知识水平可以直接应用前面的公式（7.7）来度量，只不过这时的W是偏好映射的基数：

而且仍然有Wmin＝1以及Wmax＝m，分别对应区分最细以及不能区分的情况。这样，一个偏好映射PM＝（PMi）n×1中包含的用于区分的知识水平为

类似地，偏好映射PM＝（PMi）m×1中包含的无知程度为

相应地，也有KPM∈［0，ln m］，IPM∈［0，ln m］，以及

进而，偏好映射PM＝（PMi）n×1中包含的香农信息熵为

将公式（7.17）与物理学中的玻尔兹曼熵公式S＝kBlnΩ比较，可以看出，弱序偏好中的香农熵公式与物理学中的玻尔兹曼熵公式有着相同的形式：(www.xing528.com)

其中，k＝ln 2，W＝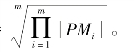

下面给出一个算例。

例7.2　假设方案集为X＝｛x1，x2，…，x5｝，专家集为｛专家1，专家2，专家3｝，专家基于弱序给出的偏好序为

专家1：x1≻x2～x3≻x4～x5，

专家2：x1≻x2～x3～x4≻x5，

专家3：x1～x2≻x3≻x4≻x5。

其对应的偏好映射分别为

应用式（7.14），3位专家给出的偏好序中包含的用于区分方案的知识水平分别为

以上计算结果表明，专家3的偏好中包含的区分知识最多，因而区分最细，这个结果与专家给出的偏好中所包含的区分信息是一致的。