基于不动点的多准则决策与群决策中的度量公式与案例分析

等价关系和弱序关系是与人们的认识行为紧密联系的两种关系。日常生活中，人们需要识别事物以及做出最优选择。在识别事物的时候，人们用的是等价关系，尽管可能并没有意识到这一点。在做出理性选择的时候，人们往往基于弱序关系。下面讨论与等价关系和弱序关系有关的知识度量问题。

有限集合上的一个等价关系对应着集合的一个划分，这种划分由不交的等价类构成，两个事物是等价的当且仅当它们处于一个等价类中［89］。

考虑建立在有限集合X＝｛x1，x2，…，xm｝上的等价关系～，xi～xj表示xi和xj是等价的、处于一个等价类中。令［xi］表示xi对应的等价类，［xi］＝∈X，xj～xi｝由集合X中所有与xi等价的元素构成。显然，知识越多，分类越细，不确定性越小；如果一无所知，则不能区分，此时不确定性最大。因此，可以用元素的等价类的基数来刻画不确定性。

令

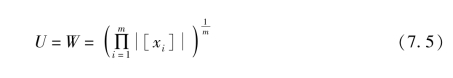
则Wmin＝1和Wmax＝n，分别对应着具有完全知识（因而具有最细的分类，不确定性最小）和完全不具有知识（因而所有的元素都不能区分，不确定性最大）。这样式（7.3）的边界条件为

因而，公式（7.3）化为

从而

类似地，式（7.4）的边界条件为

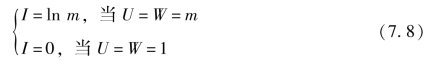
因而，公式（7.4）化为

从而

(www.xing528.com)

因为1≤W≤m，所以0≤K≤ln m，0≤I≤ln m。

由式（7.7）和式（7.9）有：

定理7.1　在认知过程中的知识水平与无知水平有着互补关系

以上定理意味着“知识越多，无知越少”。

下面给出一个算例。

例7.1　假设有5个鸡蛋，X＝｛egg1，egg2，egg3，egg4，egg5｝，两个人｛张三，李四｝被要求用他们各自的衡器对鸡蛋称重。张三和李四报告的称重结果如表7.1所示。现在我们计算张三和李四在识别鸡蛋的重量上所体现出来的知识水平。

表7.1　称重结果（以克为单位）

建立在张三的称重结果上的鸡蛋等价类为：［egg1］＝｛egg1｝，［egg2］＝｛egg2，egg3｝，［egg3］＝｛egg2，egg3｝，［egg4］＝｛egg4，egg5｝，［egg5］＝｛egg4，egg5｝。应用式（7.7），张三所提供的称重结果包含的对区分鸡蛋重量的知识水平为

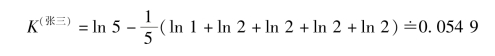
建立在李四的称重结果上的鸡蛋等价类为：［egg1］＝｛egg1｝，［egg2］＝｛egg2｝，［egg3］＝｛egg3｝，［egg4］＝｛egg4，egg5｝，［egg5］＝｛egg4，egg5｝。应用式（7.7），李四所提供的称重结果包含的对区分鸡蛋重量的知识水平为

从计算结果可以看出，李四的称重结果所包含的用于区分鸡蛋重量的知识水平比张三的结果所包含的知识水平要高，即李四的结果的区分度要高，或者说李四的衡器的精度要高于张三所用的衡器的精度。这个结果与表7.1中的数据所反映的事实是相符的。

由知识水平的公式可以看出，知识水平的数值与事物集合的基数m有关。为了消除m的影响，可以对知识数值进行归一化。在采用极差归一化时，归一化了的知识水平公式为

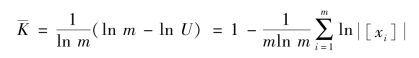
应用归一化了的知识水平公式，可以算出例7.1中张三和李四知识水平的相对差异为0.172 3。