不动点决策和群决策：共识的半群结构

共识的偏好映射构成集合，如果在该集合上定义了如前所述的交运算，则有可能形成了一个代数系统，而且是可交换半群代数系统。下面给出简单叙述。

在数学上，一个半群〈S，°〉是指集合S以及建立在其上的二元运算°一起构成的代数系统，其中运算°是可结合的［39］。

令对象集为X＝｛x1，x2，…，xn｝，专家的偏好是基于对象集上的弱序（weak order）给出的偏好序。则如前所述，专家的偏好可以用偏好映射来表示（定义5.3）。

令关于对象集X的所有可能的偏好映射构成的集合为Ω，并称Ω为X的偏好空间（preference space）。偏好空间中的任一点都是关于对象集X中的对象的一个偏好映射，Ω中的偏好映射都有n个分量。为了方便，我们称有n个分量的偏好映射为n维的偏好映射。对PM∈Ω，记PM＝［PMi］n×1。

偏好空间Ω中包含的是建立在对象集X＝｛x1，x2，…，xn｝上的所有可能的偏好序（建立在弱序基础上的），当n确定时，Ω中包含的偏好映射的数目（记为）是确定的，这个数目就是建立在集合X＝｛x1，x2，…，xn｝上的所有可能的、允许平局情形下的偏好序，其与n的对应关系（n＝3，4，5，6，7）见表6.1。

表6.1　当n＝3，4，5，6，7时偏好空间中的偏好映射数目［44］

对于表6.1中建立在集合X＝｛x1，x2，…，xn｝上的所有可能的弱序数目，可以采用下式进行计算［80］：

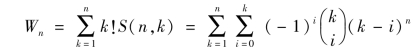
其中S（n，k）是第二类斯特林（Stirling）数，其含义是在把n个元素的集合划分为k个非空子集时，所有可能的划分个数。

对偏好空间Ω，在其上建立如第5章所述的交运算∩，对PM（1），PM（2）∈Ω，建立运算

显然，以上定义的交运算满足交换律和结合律。需要注意的是，偏好空间Ω以及建立在其上的交运算∩并不构成代数系统，因为偏好空间Ω包含所有可能的n维偏好映射，但两个偏好映射的交不一定还是一个偏好映射，即不满足运算的封闭性。

但是由定理5.5可知，对共识的偏好映射，它们的交仍然是一个偏好映射，即在共识的前提下，交运算具有封闭性。因此有以下结论。

结论6.3　设H⊂Ω，如果H中的偏好映射是共识的，即

且Η中任意两个偏好映射的交仍然在Η中，即

则〈Η，∩〉构成一个可交换的半群代数系统。(https://www.xing528.com)

设偏　好　映　射PM（1）＝…，PM（m）＝且这m个偏好映射是共识的。由推论5.2和定义5.5知道它们的交

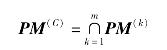
也是一个偏好映射。则由结论6.3有以下结论。

结论6.4　设PM（1）＝…，PM（m）＝是m个共识的偏好映射，且它们的共识偏好映射为PM（C）＝则

构成一个交换半群，且共识映射PM（C）是该半群的零元，其中

其中“｛PM（s，t）PM（s）∩PM（t），s＜t｝∪…”表示下列集合的并：由｛PM（1），PM（2），…，PM（m），PM（C）｝中元素两两的交组成的集合，由两两的交组成的集合中元素的两两的交组成的集合，由两两的交组成的集合中元素的两两的交组成的集合的元素的两两的交组成的集合……直到两两的交产生不出新的偏好映射为止。注意，“｛PM（s，t）PM（s）∩PM（t），s＜t｝∪…”涉及的集合是有限的，因为两两的交的过程不可能永远持续下去，在共识的前提下、有限步骤内一定能到达不能产生新的偏好映射这一结果。

例如，建立在方案集｛x1，x2，x3，x4｝上的如下4个偏好映射是共识的：

它们的共识映射为

两两的交映射为

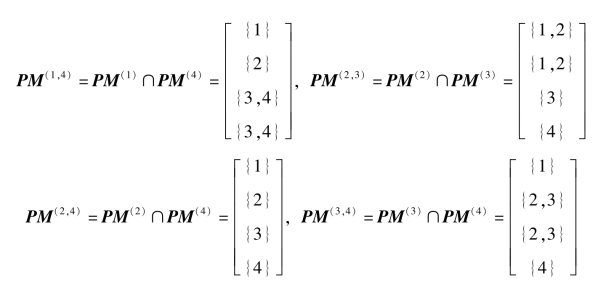
以上只产生一个新的偏好映射PM（3，4）。但PM（3，4）和其他偏好映射的交则没有产生新的偏好映射，从而

可以验证由以上的集合Η和交运算一起构成的代数系统〈Η，∩〉是交换半群，且零元是共识映射PM（C）＝因为PM（C）与H中的任一偏好映射的交仍然等于PM（C）。