不动点与群决策-基于不动点的多准则决策与群决策

设Ω为一个有限集，∅是空集，记Ω的幂集为2Ω，则对任意A，B，C∈2Ω＼∅，如果定义

则式（6.5）是一个距离测度，即它满足如下性质：

（1）DIFFERENCE（A，B）≥0，且DIFFERENCE（A，B）＝0，当且仅当A＝B。

（2）DIFFERENCE（A，B）＝DIFFERENCE（B，A）。

（3）DIFFERENCE（A，B）+DIFFERENCE（B，C）≥DIFFERENCE（A，C）。

以上度量DIFFERNCE也被称为Marczewski-Steinhaus距离，是描述非空有限集合之间的距离测度，该式是由Marczewski和Steinhaus在20世纪50年代建立的［76］。该距离已经在很多领域得到了应用，比如在粗糙集理论与方法中［77］。

自从Marczewski-Steinhaus距离提出以来，文献中（包括提出该距离的原始文献［76］）出现了很多证明该距离为测度的方法、过程，比如1971年出现在Nature的文献［78］，尽管该文并未引用Marczewski和Steinhaus的原始文献［76］。本节给出Marczewski-Steinhaus距离是距离测度的另一个证明，该证明过程不同于已有方法的证明过程。

引理6.1　设Ω为一个有限集，∅是空集，记Ω的幂集为2Ω。则对任意A，B，C∈2Ω＼∅，有

即

证明：思维方法相当于考察每一种组合（A，B，C）。但是，在思考的时候，任选一个集合对（A，C），并固定它的值，然后考虑B的变化对式子取值的影响。这样的思维过程也相当于考察了每一种组合（A，B，C），因为集合对（A，C）是任选的，B又是变化的。

分两种情况：

（1）A∩C＝∅：对每一个集合对（A，C），为了使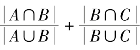最大，在已知A∩C＝∅的前提下考察（A，C），我们能够选择B＝A或C或A∪C来使达到它的最大值。此时最大值是

因为A∩C＝∅即＝0，从而此时的最大值即

（2）A∩C≠∅：类似于以上分析，现在已知条件是A∩C≠∅，对每一个集合对（A，C），选择合适的B使达到最大值。从第一项来说，应该尽可能使B在A中；从第二项来说，应该尽可能使B在C中。考虑3种情况：

①令B＝A∩C，此时值为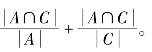

②令B＝A，此时值为1+

（3）令B＝C，此时值也为1+(www.xing528.com)

现在考察在A∩C≠∅前提下，的大小关系。

令＝r，则有r≤min｛p，q｝。利用＝p+q-r，则

由于pq-［（p+q）r-r2］＝r2-（p+q）r+pq，是关于r的一元二次函数，同时一元二次方程r2-（p+q）r+pq＝0的两个解恰为p和q。由初等代数的韦达定理可知，在r≤min｛p，q｝时，一元二次函数r2-（p+q）r+pq的值是非负的，即r2-（p+q）r+pq≥0，从而pq-［（p+q）r-r2］≥0，从而pq≥［（p+q）r-r2］，从而≥0，从而

因而，1+的最大值。证毕。

定理6.2　设Ω为一个有限集，∅是空集，记Ω的幂集为2Ω。则对任意A，B，C∈2Ω＼∅，如果定义

则有（从现在开始，简记DIFFERENCE（A，B）为D（A，B））：

（1）0≤D（A，B）≤1（非负性）。

（2）D（A，B）＝D（B，A）（对称性）。

（3）D（A，B）+D（B，C）≥D（A，C）（三角不等式）。

即指标DIFFERENCE（A，B）是集合2Ω＼∅上的一个距离测度。

证明：

前两条性质显而易见是满足的，因此下面只证明第三条性质。

根据指标DIFFERENCE的定义，三角不等式可以改写为

因而只需证明式（6.6）是成立的。由引理6.1知

因而式（6.6）成立。证毕。