多准则决策中的偏好映射方法简介

在对策论中，纳什均衡是一个基本概念。本节说的对策，特指有限、静态、纯策略的非合作对策。纳什均衡的描述如下（译自文献［70］）：

“定义23.1在参与人偏好是偏好序的静态对策中，一个策略组合a*，如果对每一个参与人i以及参与人i的每一个策略ai来说，策略组合a*带来的收益都至少和策略组合带来的一样好，其中参与人i选择策略ai而其他每个参与人j的策略为，或等价地说，对每一个参与人i以及参与人i的每一个策略ai，都有ui（a*）≥ui（ai，），其中ui是代表参与人i的偏好的支付函数，则策略组合a*是一个纳什均衡。”［70］

令Bi（a-i）为参与人i对其他参与人策略组合a-i的最优反应策略集合，纳什均衡也可以用最优反应函数做如下定义（译自文献［70］）：

“定义36.1在参与人偏好是偏好序的静态对策中，一个策略组合a*是纳什均衡，当且仅当a*中每一个参与人的策略都是对其他参与人策略组合的最优反应

以上的定义最早出现在Nash 1950年发表的文章里［71，72］。以上的定义给我们如下启示：

（1）在一个序偏好的有限静态对策中，一个参与人的对其策略的序偏好可以用偏好映射来表示，因为偏好映射能有效地描述决策者的序偏好。

（2）序偏好的有限静态对策中纳什均衡有可能用偏好映射进行描述。

（3）纳什均衡的某些存在性条件有可能通过偏好映射来检验。

下边我们进行讨论。

令G＝｛S1，S2，…，Sn；u1，u2，…，un｝表示一个序偏好的有限静态对策，N＝｛1，2，…，n｝表示参与人的集合，｝表示参与人i的策略集，ui是对应参与人i的序偏好的支付函数。在静态的情况下，对策与参与人的行动顺序没有关系，因此，策略组合（s1，s2，…，sn）等价于（si，s1，s2，…，si-1，si+1，…sn）＝（si，s-i）。

令s为一个策略组合，其中参与人i的策略为si。令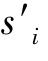代表参与人i的策略中的任一策略，表示这样的一个策略组合，其中参与人i的策略为s＇i，而其他人的策略用s-i来表示。

当除了参与人i以外的其他人的策略组合为s-i时，参与人i在选择不同的策略时的收益分别为ui。令基于参与人i对这些不同策略的收益的偏好序的偏好映射为PM（i），该偏好映射的第k个分量（对应于参与人i的第k个策略sik的排序位置）记为，并且记偏好映射对应的最偏好行动集PAS（preferred action set）为

注意本小节中最偏好行动集和上小节中最偏好方案集都简称为PAS，这是一个有趣的巧合，实际上，下边读者将会看到，对策中的最偏好行动集与群决策中的最偏好方案集起着相同的作用。

Osborne对纳什均衡的定义式（5.21），可以用偏好映射描述如下。

定义5.23　令G＝｛S1，S2，…，Sn；u1，u2，…，un｝表示一个序偏好的有限静态对策，N＝｛1，2，…，n｝表示参与人的集合，Si＝表示参与人i的策略集，ui是对应参与人i的序偏好的支付函数。一个策略组合s*＝如果对于每一个参与人i及其每一个策略，在其他参与人采用的前提下参与人i在采用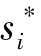时至少跟采用其他策略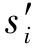一样好时，就称s*是一个纳什均衡。数学上描述为

或等价地

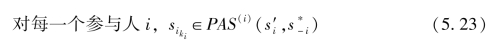
有下列结论。

定理5.9　如果s*＝是纳什均衡，

则

证明：因为s*＝是纳什均衡，由式（5.23）(www.xing528.com)

从而

即

证毕。

由定义5.23可以得出一个应用偏好映射寻找静态纯策略对策的纳什均衡（如果存在的话）的方法：

（1）对每一个策略组合（s1，…，si，…，sn）∈S1×…×Si×…×Sn，按以下步骤操作。

①写出每一个参与人对应于其偏好的偏好映射

②得到每一个参与人的最偏好方案集

③对每一个参与人，检查公式（5.23）即si∈是否成立。如果成立，则当前的策略组合是一个纳什均衡。

（2）写出所有的纳什均衡。

下面以对策中的经典问题“囚徒困境”为例说明上述过程。

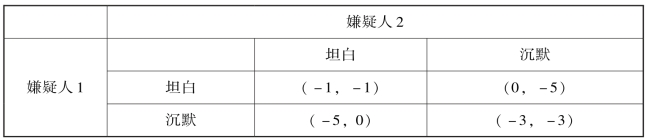
两个犯罪嫌疑人被关在独立的囚室中，检察官了解他们的基本罪行，但缺乏足够的证据对二人的犯罪进行罪有应得的惩罚，除非他们之中至少有一个坦白交代。每个嫌疑人可选择的策略是或者坦白或者保持沉默。在这两种可选策略下两人可能得到的宣判结果如下：

①如果两个人都保持沉默，则各判1年。

②如果两个人都坦白，则各判3年。

③如果一个坦白、一个沉默，则坦白的得到释放、沉默的将被判5年。

这两个人组成了一个有限静态对策问题G＝｛1，2；｛坦白，沉默｝，｛坦白，沉默｝｝，不同策略对应的收益情况可以用表5.2给出。

表5.2　两个参与人的策略-收益

为了直观，将计算过程总结在表5.3中，可以看出策略组合（坦白，坦白）是该对策的唯一纳什均衡。

表5.3　应用偏好映射计算纳什均衡的过程

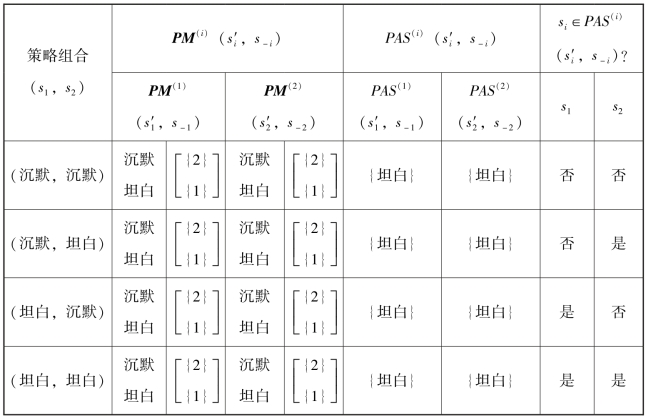
需要说明的是，应用偏好映射寻找纳什均衡的计算量，比传统的寻找纳什均衡方法的计算量要大得多，原因在于构造偏好映射需要对一个参与人的所有策略进行排序（假如采用冒泡法对n个数进行全排序，计算复杂度为O（n2）），而传统的寻找纳什均衡的方法的过程中只需从一个参与人的所有策略中找出最好的（从n个数中找出最好的，仅需n-1次比较）。但是，本节的目的不是提供一个新的求纳什均衡的方法，而是在于通过偏好映射描述群决策中的可能均衡和对策中的纳什均衡，从而通过考察它们的相似性揭示群决策与对策的某种相似性联系。