Cook-Seiford距离公理系统的比较与分析

共识间距满足的公理系统和Cook-Seiford距离满足的公理系统之间的主要区别体现在公理4.1和公理5.1、公理4.3和公理5.3，而恰恰是这两组公理的不同，体现了作为描述共识差异的数学工具，准测度比传统的距离测度更具有优势。下面进行比较和分析。

（1）Cook-Seiford距离是一个测度，因为它满足测度的要求：非负性、对称性和三角不等式。共识间距是个准测度，它只满足非负性和对称性，不一定满足（数学上说就是不满足）三角不等式。

（2）两个Cook-Seiford向量之间的Cook-Seiford距离等于0，当且仅当两个Cook-Seiford向量相等（完全一样）。数学上描述，令CS（1）＝为两个Cook-Seiford向量，d（CS（1），CS（2））＝0当且仅当∀i（

两个偏好映射之间的共识间距等于0，当且仅当两个偏好映射是共识的（定义5.4）。数学上描述，令PM（1）＝为两个偏好映射，Δ（PM（1），PM（2））＝0当且仅当∀i

（3）Cook-Seiford距离满足三角不等式，而共识间距并不总是满足三角不等式。

比如，考察两个方案的3种可能排序：A1≻A2，A1～A2和A2≻A1。对应的Cook-Seiford向量分别为

它们之间的Cook-Seiford距离为：d（CS（1），CS（2））＝1，d（CS（2），CS（3））＝1，d（CS（1），CS（3））＝2。从而，d（CS（1），CS（2））+d（CS（2），CS（3））≥d（CS（1），CS（3））。

三种排序A1≻A2，A1～A2和A2≻A1对应的偏好映射分别为

它们之间的共识间距为：Δ（PM（1），PM（2））＝0，Δ（PM（2），PM（3））＝0，Δ（PM（1），PM（3））＝2。从　而，Δ（PM（1），PM（2））+Δ（PM（2），PM（3））＜Δ（PM（1），PM（3））。

正是以上的差别保证了共识间距作为描述个体偏好差异的指标比Cook-Seiford距离更具有优势。下面举例分析。

（1）共识间距是一个能描述群决策中共识的指标：如果个体对某一个方案的排序有公共位置，那么就说这些个体在这个方案的偏好上有共识，也就是说，在这一方案上个体的偏好没有间距，否则，共识间距将被观察到。定义5.4通过检查偏好映射相同位置的分量的交集是否不为空，描述了这种共识。

举例来说，考虑有3个人（张三，李四，王五）和2种饮品（咖啡A1，茶A2），偏好如下：(www.xing528.com)

①张三喜欢咖啡胜过喜欢茶，即，A1≻A2。

②李四对茶和咖啡一样喜欢，即，A1～A2。

③王五喜欢茶胜过喜欢咖啡，即，A2≻A1。

显然张三和李四之间有共识，因为如果作为主人为张三和李四2位客人准备了咖啡，则张三和李四都会满意。同样地，李四和王五也有共识。但是，张三和王五之间却没有共识。个体的偏好可以用偏好映射表示为：

张三对应的偏好映射：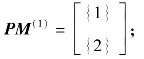

李四对应的偏好映射：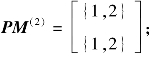

王五对应的偏好映射：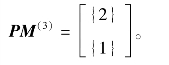

通过计算共识间距的公式（5.6），有Δ（PM（1），PM（2））＝0，Δ（PM（2），PM（3））＝0，Δ（PM（1），PM（3））＝2。可以看出，共识间距是反映了共识的：张三和李四之间有共识，所以没有共识间距，他们之间的共识间距为0；同样，李四和王五之间也因为有共识因而没有共识间距；但张三和王五之间没有共识，因而共识间距大于0。但是，如果用Cook-Seiford距离则反映不出这3个人偏好之间的共识，因为Cook-Seiford距离为0当且仅当个体偏好一样，这3个人的偏好之间的Cook-Seiford距离分别为：d（CS（1），CS（2））＝1，d（CS（2），CS（3））＝1，d（CS（1），CS（3））＝2。

（2）如前所述，共识间距不一定满足三角不等式，这不是缺点，恰恰是反映了群决策中事实的一个优势，因为“群决策中共识是不传递的”！正如上例中，张三和李四有共识，同时李四和王五有共识，但张三和王五没有共识！共识间距能有效地反映出群决策中的这个事实，上例中，对共识间距来说，三角不等式就不满足，即Δ（PM（1），PM（2））+Δ（PM（2），PM（3））＜Δ（PM（1），PM（3））。显然，总是要求满足三角不等式的Cook-Seiford距离不能反映“群决策中共识不传递”这一事实！

总之，通过对共识间距和Cook-Seiford距离各自满足的公理体系的比较分析，可知，共识间距能有效地反映出群决策中的两个事实：①个体偏好不一样，却可能有共识；②群决策中的共识不是传递的。但Cook-Seiford距离不能描述群决策中的这两个基本事实。