本小节给出偏好映射与Cook-Seiford向量的相互转换方法,并说明这种转换的内禀一致性,即从表示允许平局的偏好序上来说是等价的[69]。
由于偏好映射的分量表示方案排序的所有可能位置,而Cook-Seiford向量的分量表示的是这些可能位置的中心点。因此有以下定义或者转换方法。
定义5.20 设PM=[PMi]n×1为一个偏好映射,它对应的Cook-Seiford向量为CS=[CSi]n×1,其中

比如,有如下两个偏好映射

由式(5.16),它们对应的Cook-Seiford向量为

下边给出Cook-Seiford向量转化为偏好映射的方法。
定义5.21 设CS=[CSi]n×1是一个Cook-Seiford向量,它对应的偏好映射为PM=[PMi]n×1,其中
![]()
并且

这里ci代表PMi的中心,di是与方案xi平局的方案的数目,ai是偏好映射分量PMi中元素的最小值,bi是偏好映射分量PMi中元素的最大值。
比如,对本节前面两个Cook-Seiford向量CS(1)和CS(2)应用公式(5.17)和式(5.18)求它们对应的偏好映射,计算过程和结果总结在表5.1中。
表5.1 Cook-Seiford向量转换为偏好映射的计算实例(https://www.xing528.com)

从前面的算例可以看出,应用本节给出的转换公式,从一个偏好映射(Cook-Seiford向量)可以得出它对应的Cook-Seiford向量(偏好映射);然后,变换后的Cook-Seiford向量(偏好映射),又可以变换回原来的偏好映射(Cook-Seiford向量)。这说明这两种偏好信息的表示形式是等价的,因为:一个允许平局的偏好序,是基于建立在方案集上的弱序关系的,对应着唯一一个方案集上的有序划分,而偏好映射和Cook-Seiford向量都是允许平局的偏好序的有效表示方式。图5.2以偏好序A1≻A2~A3≻A4为例说明了这两种表示方式的等价性。

图5.2 偏好序与偏好映射和Cook-Seiford向量的关系
下面的定理进一步说明了这两种偏好信息之间相互转换的内禀一致性。
定理5.8 设PM=[PMi]n×1和CS=[CSi]n×1分别是一个偏好映射和一个Cook-Seiford向量,假设偏好映射的分量为PMi={pmi1,pmi2,…,pmiLi},记sum(PMi)=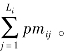 则
则
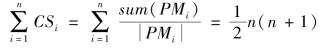
证明:由性质5.1知,一个偏好映射对应于集合{1,2,…,n}的一个划分,一个分量是一个方案对应的等价类,因此 (1+2+…+n)=
(1+2+…+n)=![]()
从式(5.18)有CSi=![]()
由于sum(PMi)=ai+(ai+1)+(ai+2)+…+bi=![]() 因而
因而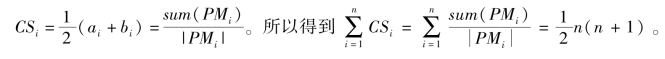 证毕。
证毕。
比如,考虑如下的偏好映射和Cook-Seiford向量

由定理5.8有
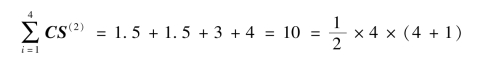
和
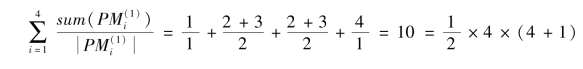
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




