基于不动点的决策和群决策

首先引入偏好映射矩阵。

定义5.6　设有m个建立在方案集X＝｛A1，A1，…，An｝上的偏好映射k＝1，2，…，m。以偏好映射为列向量（注意不是普通代数意义上的向量）构成的矩阵称为偏好映射矩阵：

规定偏好映射矩阵M和一个偏好映射Γ＝［Vi］n×1之间的交运算如下：

有以下结果。

定理5.6　设有m个偏好映射k＝1，2，…，m，其构成的偏好映射矩阵为M。这些偏好映射是共识的当且仅当存在偏好映射Γ＝［Vi］n×1满足如下的不动点方程（具有f（x）＝x的形式）：

M∩Γ＝Γ

证明：充分性。按照偏好映射矩阵与偏好映射相交的运算规则可知，如果不动点方程满足，则有

因为Γ＝［Vi］n×1是个偏好映射，由性质5.1可知，Vi≠∅。因而由

进而有

由共识的数学定义可知，已知的m个偏好映射k＝1，2，…，m，是共识的。

必要性。如果已知的m个偏好映射是共识的，由推论5.2可知，是一个偏好映射。令Γ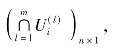＝由偏好映射矩阵与偏好映射的相交运算规则，可知

即(www.xing528.com)

成立。证毕。

当多个偏好映射是共识的时，可能存在多个偏好映射作为不动点满足不动点方程。下边的结论指出，共识偏好映射对应的是不动点方程的一个特殊不动点。先引入偏好映射的基数的概念。

定义5.7　设Γ＝［Vi］n×1是一个偏好映射，其基数定义为

由性质5.1显然可推出以下结论。

性质5.2　若Γ＝［Vi］n×1为一个偏好映射，则n≤

定理5.7　设有m个偏好映射k＝1，2，…，m，如果它们是共识的，则存在且只存在一个基数最大的偏好映射，作为已知的m个偏好映射构成的偏好映射矩阵满足的不动点方程的解，而且该基数最大的偏好映射恰为前面定义的共识偏好映射：

证明：令Γ＝由于已知的偏好映射是共识的，由推论5.2知，Γ是一个偏好映射。由定理5.6的证明过程可知，Γ是一个不动点。

由Γ的式子、不动点方程的式子以及集合交运算的性质可知，Γ是满足不动点方程的所有不动点中基数最大的。存在性成立。

下面证明唯一性，采用反证法。假设存在两个基数都为最大值的偏好映射都是不动点，且由于都是不动点方程的解，则有若则至少存在一个分量对∃i*和都满足不动点方程，由集合的交运算以及集合的性质可知，如　果即此时至少有一个是的真子集。不失一般性，假设则因而在知道⊆的前提下，必然有这与假设的基数是最大值矛盾。因而基数最大的不动点是唯一的。证毕。

由定理5.7知道，共识时不动点方程存在基数最大的不动点，且基数最大的不动点是唯一的，其恰恰为定义5.5定义的共识映射。实际上，共识映射包含的共识偏好信息是最多的，这也是称其为共识映射的原因。