共识偏好映射及其性质证明

可以证明，当两个或者多个偏好映射是共识的时，它们的交也是一个偏好映射，即逐条验证性质5.1中的条目，这个结论的证明需要一些准备工作。读者如果对证明不感兴趣，可以略过证明而只理解结论的含义和意义。

由性质5.1可知，一个偏好映射对应着集合I＝｛1，2，…，n｝的一个划分，不同分量代表着不同的划分块，每一个划分块中，若包含多个元素，则这些元素是连续自然数，同一个偏好映射的任意两个分量或者相等、或者不交。偏好映射的一个分量表示一个方案可能的排序位置，一个分量中的自然数个数表示有多少个方案和这个分量对应的方案是处于平局的（无差异的）。在一个偏好映射的分量中，一个分量作为集合出现的次数恰恰是该集合的基数，表示这些相同的分量对应的不同方案处于平局状态。有以下结果。

定理5.2　设（Ui）n×1和（Vi）n×1是两个偏好映射，则

（1）存在满足｛1｝必满足如下三种关系中的一种：

（2）存在必满足如下三种关系中的一种：

证明：由偏好映射的性质（性质5.1）可知：一个n维的偏好映射代表集合｛1，2，…，n｝的一个划分，偏好映射的不同分量对应不同的划分块，且每个划分块中包含的是连续自然数（在划分块包含的元素数目大于1时）。因此，每个偏好映射中必然存在包含元素1的分量，且该分量中的元素为以1为最小元素的连续自然数；同时，每个偏好映射的分量中必然存在包含元素n的分量，且该分量中的元素为以n为最大元素的连续自然数。由于偏好映射的分量都是集合，因此定理成立。

定理5.3　设（Ui）n×1和（Vi）n×1是两个偏好映射，且是相互共识的，即∀i（Ui∩Vi）≠∅。则

（1）如果Ui⊆Vi或者Vi⊆Ui，则Ud＝Ui，Vd＝Vi，d∈I｝

（2）

（3）如果Ur∩Vs≠∅，r≠s，则∃d（Ud∩Vd≠∅），其中Ud＝Ur，Vd＝Vs。

说明：本定理的第一条是第二条的特例，为易于理解证明过程，将其分别列出。

证明：（1）只考查Ui⊆Vi的情况，而在Vi⊆Ui情况下的讨论类似。

由偏好映射的性质（性质5.1）的第3条可知：

一个偏好映射的分量之间有如下关系：要么相等、要么不交。

因此，在已知Ui⊆Vi的条件下，Ui只能与偏好映射（Vi）n×1中的等于Vi的分量的交集不为空，即（Ui∩Vj≠∅）→（Vj＝Vi）。

又由偏好映射的性质（性质5.1）的第5条可知：偏好映射（Ui）n×1的分量中，等于Ui（在集合相等的意义下）的分量个数为

因此，在已知共识即∀k（Uk∩Vk）≠∅和Ui⊆Vi的条件下，偏好映射（Ui）n×1中个等于Ui的分量只能与（Vi）n×1中等于Vi的分量有交集，且有

定理的第一条成立。

（2）本条目的证明应用偏好映射的性质（性质5.1）、已知是共识的这一前提条件以及本定理的第一条。

由于一个偏好映射的不同分量构成集合｛1，2，…，n｝的一个划分，偏好映射的一个分量对应一个划分块，且每个划分块中包含的是连续自然数。因此，将一个偏好映射（Ui）n×1对应的划分块，按照各自最大元素升序排成一列，则包含1的划分块排在最上面、包含n的划分块排在最下面。

令（Ui）n×1对应的划分包含u个划分块，划分块中的最大元素从小到大依次为s1，s2，…，su，其中s1是包含1的划分块中的最大元素，同时也是包含1的划分块中的元素数目；su是包含n的划分块的最大元素，显然su＝n，包含n的划分块中的元素数目为su-su-1。从而，对于（Ui）n×1对应的划分块，其各自包含的元素数目为：当u＝1时，（Ui）n×1只对应一个划分块，其中包含的元素数目为n；当u＞1时，第一个划分块（即包含1的划分块）中的元素数目为s1，其他划分块中的元素数目满足：对第k个划分块，其中元素数目为sk-sk-1，k＝2，3，…，u。为了叙述方便，将（Ui）n×1对应的u个划分块，按照各自所包含的最大元素升序排列，并记为BUs，s＝1，2，…，u。显然有1≤maxBUj＜maxBUk≤n，j＜k。

同样，令（Vi）n×1对应的划分包含v个划分块，划分块中的最大元素从小到大依次为t1，t2，…，tv，其中t1是包含1的划分块中的最大元素，同时也是包含1的划分块中的元素数目；tv是包含n的划分块的最大元素，显然tv＝n，包含n的划分块中的元素数目为tv-tv-1。当v＝1时，（Vi）n×1只对应一个划分块，其中包含的元素数目为n；当v＞1时，第一个划分块（即包含1的划分块）中的元素数目为t1，其他划分块中的元素数目满足：对第k个划分块，其中元素数目为tk-tk-1，k＝2，3，…，v。为了叙述方便，将（Vi）n×1对应的v个划分块，按照各自所包含的最大元素升序排列，并记为BVt，t＝1，2，…，v。显然有1≤maxBVj＜maxBVk≤n，j＜k。

对（Ui）n×1，从包含1的划分块对应的分量开始，分情况验证（应用本定理的第一条），然后验证第二个即包含s2的划分块对应的分量，等等，直到包含n的划分块对应的分量为止。证明的逻辑框图如图5.1所示。

图5.1　定理5.3（2）证明的逻辑图

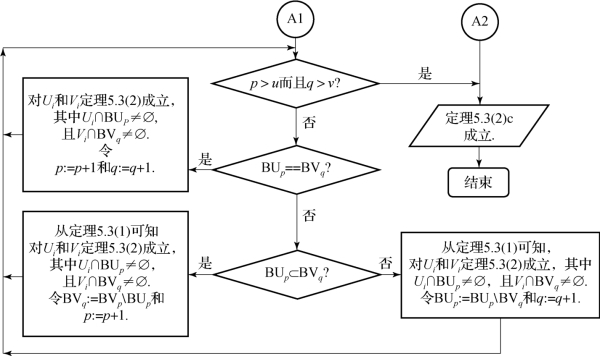
图5.1　定理5.3（2）证明的逻辑图（续）

（3）本条目直接可以从定理5.3（2）的证明过程推知。

定理5.3（2）的含义是，两个偏好映射在共识的情况下，一个方案对应的两个偏好映射的分量对的交集不为空，则与该已知分量对相等的分量对的个数恰为已知分量对的交集中的元素个数。(www.xing528.com)

定理5.3（3）说明，如果两个偏好映射是共识的，当有分量的交叉对不为空时，一定存在着这样的平行对，该平行对的分量与交叉对的分量对应相等。该结论在以下的推论5.1中用于消去交叉对的交。

由定理5.3（3）有以下推论。

推论5.1　设（Ui）n×1和（Vi）n×1是两个偏好映射，且是相互共识的，即∀i（Ui∩Vi）≠∅。则有

定理5.4　设（Ui）n×1和（Vi）n×1是两个偏好映射，且是相互共识的，即∀i（Ui∩Vi）≠∅。则有

证明：因为（Ui）n×1和（Vi）n×1是两个偏好映射，由性质5.1可知

从而

由集合的运算可知

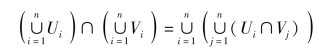
从而

把推论5.1的式子代入，有

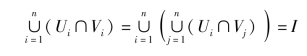
证毕。

定理5.5　如果两个偏好映射是共识的，则它们的交也是一个偏好映射。即，令（Ui）n×1和（Vi）n×1为两个偏好映射，如果∀i（Ui∩Vi≠∅），令（Ui）n×1∩（Vi）n×1＝（Wi）n×1则（Wi）n×1也是一个偏好映射。

证明：只需逐条验证性质5.1的条件是否被（Wi）n×1满足（因为性质5.1也是偏好映射的充要条件）。

（1）由于Ui和Vi是偏好映射的分量，因而Ui⊆I，Vi⊆I，且Ui≠∅，Vi≠∅。在已知∀i（Ui∩Vi≠∅）和Ui∩Vi＝Wi的前提下，显然有Wi⊆I且Wi≠∅。

（2）由定理5.4可知，

（3）由于Wi∩Wj＝（Ui∩Vi）∩（Uj∩Vj）＝（Ui∩Uj）∩（Vi∩Vj），而Ui、Uj、Vi和Vj是偏好映射的分量，满足Ui＝Uj或者Ui∩Uj＝∅，以及Vi＝Vj或者Vi∩Vj＝∅，因而可知，Wi＝Wj或者Wi∩Wj＝∅。

（4）Ui和Vi是偏好映射的分量，因而Ui和Vi中包含的都是连续自然数，在已知Ui∩Vi≠∅时它们的交集也包含连续自然数，Wi包含的是连续自然数。

（5）由定理5.3（2）知，（Wi）n×1中等于Wi的分量个数为

从而（Wi）n×1满足性质5.1的所有条目。因而（Wi）n×1是一个偏好映射。

定理5.5也可以从另外一个角度来理解：两个偏好映射对应同一集合上的两个等价关系，等价关系的交仍然是等价关系；另外，两个偏好映射对应位置上的分量，对应的是同一个方案在两个等价关系下的两个等价类，如果所有对应等价类的交不为空（共识时），所有方案将在交等价关系下具有其各自的等价类，因而，共识的两个偏好映射的交也是一个偏好映射。

对于多个偏好映射满足共识条件时，由定理5.5有以下结论。

推论5.2　令有m个偏好映射k＝1，2，…，m。假设它们是共识的，即∀i则它们的交形成的序列也是一个偏好映射。

由于共识的偏好映射的交也是偏好映射，引入共识偏好映射的概念。

定义5.5　设有m个共识的偏好映射k＝1，2，…，m。称它们的交形成的偏好映射

为这些偏好映射的共识映射。