解决满意一致性标准方面的问题

引理3.2　基于乘性互补判断矩阵的层次决策模型PCbHA中所用的满意一致性标准IF pik＜pjk，THEN∀l（pil≤pjl），等价于推论2.2中的不动点方程：

∀i，j（Rowi⊕Rowj＝RowiOR Rowi⊕Rowj＝Rowj）

证明：条件IF pik＜pjk，THEN∀l（pil≤pjl）等同于∀i，j（Rowi≥RowjOR Rowi≤Rowj）。按照推论2.2中引入的符号以及乘半域中的运算，可知∀i，j（Rowi≥RowjOR Rowi≤Rowj）等同于∀i，j（Rowi⊕Rowj＝RowiOR Rowi⊕Rowj＝Rowj）。所以，条件IF pik＜pjk，THEN∀l（pil≤pjl）等价于条件∀i，j（Rowi⊕Rowj＝RowiOR Rowi⊕Rowj＝Rowj）。证毕。

引理3.2说明了：层次决策模型PCbHA中所用的满意一致性标准是个定性标准，其含义是判断矩阵的任意两行所有对应元素在大小关系上是否一致，这个满意一致性标准是非常直观、合理的，因为在一致性的情况下，第i行和第j行分别为

和

显然，在一致阵的情况下，必然有：(www.xing528.com)

（1）当ωi＞ωj时，应该有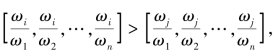即每个分量都有对应的大小关系。

（2）当ωi＝ωj时，应该有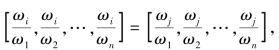即每个分量都对应相等。

对于不一致阵，采用比一致性条件放宽的∀i，j（Rowi≥RowjOR Rowi≤Rowj）来作为满意一致性标准是合理的。

由于IF pik＜pjk，THEN∀l（pil≤pjl）是个定性而不是定量条件，因而避免了AHP中的满意一致性标准的悖论。

另外，由推论2.2、推论2.4、推论2.6和引理3.2可知，乘性互补判断矩阵的满意一致性标准与加性互补判断矩阵、模糊互补判断矩阵的满意一致性标准有同构对应。