AHP中逆序问题解决：基于不动点的多准则决策与群决策

引理3.1　一致性乘性互补判断矩阵的任意一列都可以作为其对应的权重向量。

证明：按照定义，一致性乘性互补判断矩阵M＝［pij］n×n对应的权重向量W＝［ωj］n×1满足pij＝ωi／ωj，∀i，j。矩阵的第l列为

从而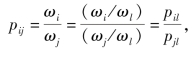，∀i，j。因而，一致性乘性互补判断矩阵的任一列都可以作为其对应的权重向量。证毕。

在下面的证明中，将应用一致阵的第一列。

定理3.1　对于基于乘性互补判断矩阵的层次决策模型PCbHA，当其中涉及的判断矩阵都是一致阵，在添加或删除一个独立方案时，不会产生逆序。

证明：假设有n个待评价方案X1，X2，…，Xn，在应用PCbHA时所建立的层次结构中有m个末端准则（末端准则意味着这些准则下边没有控制其他准则），这些末端准则相对于总目标的权重分别为ω1，ω2，…，ωm。

不失一般性，假设增加或删除一个独立方案发生在最后一个方案处，即，若添加一个独立方案，则其为Xn+1，如果是删除一个独立方案，则是删除Xn。

下面考虑删除独立方案Xn，添加情况的讨论过程类似。删除独立方案意味着，除了被删除方案以外的其他方案之间的两两比较结果在删除独立方案前后没有变化。在删除前和删除后，方案关于第k个末端准则的两两比较矩阵为(www.xing528.com)

和

由于删除的是独立方案，因而有

由于定理的条件要求涉及的判断矩阵都是一致阵，方案对末端准则的局部权重向量可以采用判断矩阵的第一列（引理3.1）。在PCbHA中，采用的是几何加权平均数据集结准则，从而，方案Xi和方案Xj（i≠n，j≠n）相对于总目标的权重比值，在删除Xn的前、后分别为

和

考虑到i＝1，…，n-1；j＝1，…，n-1；k＝1，…，m，所以

即在删除独立无关方案Xn后，其他方案之间的评价值在删除前后不但不会产生逆序，而且前后比值也不变。同样可以讨论增加独立方案的情形，可以得到同样的结论。因而定理成立。证毕。

需要强调的是，当层次决策模型PCbHA所涉及的判断矩阵都是一致阵时，PCbHA具有逆序免疫性。但是，如果其中有非一致阵，则这个结论不一定成立。但是，这从理论上说已经足够了，因为判断的非一致性意味着判断出现了矛盾，这时什么情况都可能发生。与之相比的是，对于AHP来说，当所涉及的判断矩阵都是一致阵时也可能出现逆序［2，10］。