为什么层次分析模型可行？

在多准则／多属性决策中，方案的总体评价值是采用某一集结准则通过对方案在各个准则／属性上的评价值得到的。下面分析常用的几何加权平均和算术加权平均集结准则，其中准则／属性的权重是和归一化的［11，42，43］。

1.几何加权平均对应的分解-复合

1）简单情况

一个几何加权平均可以进行如下简单变换：

以上变换可以用图3.1描述。

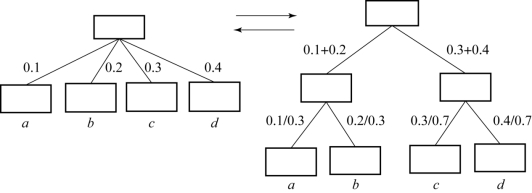
图3.1　几何加权平均对应的层次分解-复合（简单情况）

2）更一般情况

一个几何加权平均也可以进行如下变换：

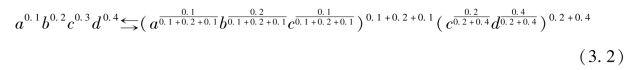
以上变换可以用图3.2描述。(www.xing528.com)

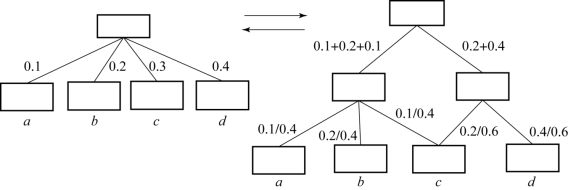
图3.2　几何加权平均对应的层次分解-复合（更一般情况）

图3.1和图3.2中，最上层的方框表示总目标，其他的方框表示准则，连线表示总目标对准则（属性）、或准则（属性）对准则（属性）的控制关系，连线旁边的数字，表示连线下端准则／属性的权重；a、b、c、d表示某个方案在末端准则或属性上的评价值。

式（3.1）和式（3.2）以及图3.1和图3.2说明：在采用几何加权平均且其中的权重向量是和归一化时，几何加权平均的等价变换形式对应着层次的分解-复合。详细一点说，式（3.1）的左式是一个几何加权平均，右式是三个几何加权平均，分别为上层的一个和下层的两个；图3.1说明了式（3.1）从左到右对应着层次的分解，从右到左对应着层次的复合。

式（3.1）和式（3.2）的区别在于，其对应的层次结构里的准则控制关系：式（3.1）对应的层次结构里，每一个下层准则只受一个上层准则控制；而式（3.2）对应的层次结构里，下层准则可以受多个上层准则的控制。

2.算术加权平均对应的分解-复合

与几何加权平均类似，算术加权平均的变换也对应着层次的分解-复合：

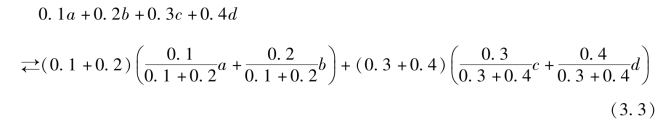
和

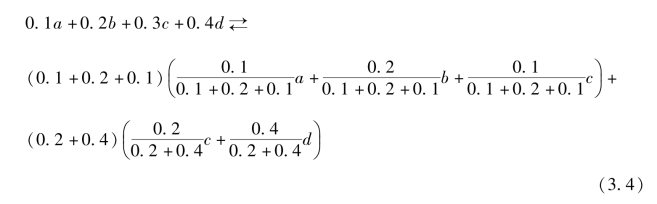
式（3.3）和式（3.4）对应的层次分解-复合也可以用图3.1和图3.2说明。

本小节的公式和图形表明，加权平均的等价变换，对应着层次的分解-复合。如果加权平均式子更复杂一些，则可以对应多种不同结构的层次模型，因此，现实决策中，如果数据集结的准则采用加权平均，则可以用层次结构模型进行分析，即将复杂问题逐层分解为简单问题解决。