基于不动点的多准则决策与群决策中的模糊互补判断矩阵性态

由模糊半域和乘半域之间的同构对应关系，可以得到模糊互补判断矩阵在模糊半域中的性态。

（1）对于一个n×n两两比较矩阵F＝（μij），其中μij∈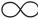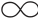（-，+），其模糊性互补和一致性条件分别为∀j，k（μjk⊗～μkj＝e～）和∀j，k，l（μjl⊗～μlk＝μjk）。

（2）对于一个一致性的模糊互补判断矩阵Fn×n＝（μjk）n×n，当一个n×1向量W＝（τj）n×1，其中τj∈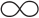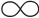（-，+），满足∀j，k∈I，μjk⊗～τk＝τj时，称其为F的一个权重向量。

定理2.13　模糊互补判断矩阵F＝（μij）n×n的模糊互补性可以用如下的不动点方程描述：（μij⊗～μji）⊗～μij＝μij，∀i，j。

定理2.14　模糊互补判断矩阵F＝（μij）n×n是一致阵的充要条件是满足如下的等幂方程：

推论2.5　如果模糊互补矩阵F是一致阵，则其中m是正整数。

定理2.15　向量W＝［τj］n×1是一致性模糊互补矩阵F＝（μij）n×n的权重向量的充要条件是如下不动点方程成立：

定理2.16　一致性模糊互补矩阵F＝（μij）n×n的行算术平均可以作为其对应的权重向量，行算术平均在半域中的表示形式为（μi1+μi2+…+μin-0.5（n-1））。

定理2.17　一致性的模糊互补判断矩阵对应着唯一的极小归一化的权重向量，即一致性的模糊互补判断矩阵存在唯一的、极小归一化的、满足方程（2.12）的不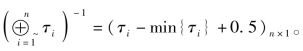动点与其对应，其形式为（τi）n×1⊗～(https://www.xing528.com)

定理2.18　在模糊半域中，加权平均的表现形式为

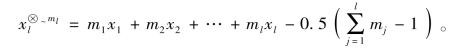
证明：由模糊半域中的乘法运算，可知

特别地，当＝1时（一般加权平均满足这个条件），有

推论2.6　对于模糊互补判断矩阵F＝（μij）n×n，定义如下操作后：

∀i1，i2

则两行比较的“不劣于”关系：

可以表示成如下的不动点方程：