基于不动点的决策与群决策

本节讨论三种互补判断矩阵的对应关系，将首先列出与三种判断矩阵有关的一些描述，部分描述已经在前面章节给出，这里以更加精练的形式同时列出三种矩阵的信息，便于读者阅读和对比。令X＝｛x1，x2，…，xn｝为对象（方案、准则等）集，I＝｛1，2，…，n｝为指标集，i，j，k等为指标变量。

乘性互补判断矩阵［1］：

（1）对于一个n×n两两比较矩阵M＝（pij），其中∀i，j（pij∈（0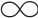，+）），其乘性互补和一致性条件分别为∀i，j（pijpji＝1）和∀i，j，k（pijpjk＝pik）。

（2）元素pij表示对象xi对xj的偏好比率。

（3）对于一个一致性的乘性互补判断矩阵M＝（pij），当一个n×1向量W＝（wk），其中wk＞0，满足∀i，j∈I，pijwj＝wi时，称其为M的一个权重向量。

加性互补判断矩阵［14］：

（1）对于一个n×n两两比较矩阵A＝（aij），其中∀i，j（aij∈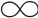（-，+）），其加性互补和一致性条件分别为∀i，j（aij+aji＝0）和∀i，j，k（aij+ajk＝aik）。(www.xing528.com)

（2）元素aij表示对象xi对xj的偏好差值。

（3）对于一个一致性的加性互补判断矩阵A＝（aij），当一个n×1向量W＝（νk）满足∀i，j∈I，aij＝νi-νj，称其为A的一个权重向量。

模糊互补判断矩阵［31］：

（1）对于一个n×n两两比较矩阵F＝（μij），其中∀i，j（μij∈［0，1］），其模糊互补和一致性条件分别为∀i，j（μij+μji＝1）和∀i，j，k（μij+μjk＝μik+0.5）。

（2）元素μij表示对象xi优于xj的程度。

（3）对于一个一致性的模糊互补判断矩阵F＝（μij），当一个n×1向量W＝（τk）满足∀i，j（μij＝τi-τj+0.5），称其为F的一个权重向量。