解决AHP中的逆序问题

AHP中的逆序（rank reversal）问题，是指用AHP对多个方案进行排序后，在增加或删除一个独立方案后，再用AHP排序，原来方案之间的序会发生改变的现象［10］。这里的“独立方案”，是指该方案的增加或删除并不改变其他方案之间的比较结果。

AHP的逆序问题可以说是学术界对AHP争议的热点问题，过去30余年中学术界对AHP的争论或多或少都与这个问题有关［2-9］。下面举例说明逆序问题，例子中的判断矩阵来源于1990年Dyer发表在Management Science上的文章［2］。

例1.1　考虑一个学院同年级、同专业、同宿舍的4名学生，应用AHP基于他们3门课的成绩做出综合排序。3门课程为数学、英语、计算机，4名学生分别为张三、李四、王五和赵六。成绩如表1.2所示，且规定3门课的权重一样。

表1.2　4名学生的成绩

应用层次分析法进行分析。首先建立目标、准则、方案的层次结构，如图1.1所示。

图1.1　成绩综合排名层次结构

由于3门课具有相同的权重，故3个准则关于总目标的归一化权重向量为［1／3　1／3　1／3］T，其中T表示矩阵或向量的转置。

先考虑张三、李四和王五3个人的排序。这3个人在数学、英语、计算机3门课上的两两比较判断矩阵分别为

以上3个判断矩阵都是一致性判断矩阵，因此任一列都可看为其对应矩阵的权重向量，从而归一化的3个权重向量为

［1／11　9／11　1／11］T，［9／11　1／11　1／11］T和［8／18　9／18　1／18］T

按照传统AHP中的算术加权平均法，张三、李四、王五3个人的排序权重为

张三：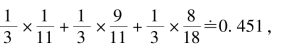

李四：

王五：

因此，当只考虑张三、李四、王五3个人在总成绩上的排名时，排序为(www.xing528.com)

李四≻张三≻王五

现在将赵六的成绩加入，考虑张三、李四、王五、赵六4个人在总成绩上的排名。注意，赵六的加入并没有改变张三、李四、王五的成绩，因而张三、李四、王五3个人之间的两两比较并没有变，或者说，赵六的加入相当于独立方案的加入。

张三、李四、王五、赵六4个人在数学、英语、计算机3门课上的两两比较判断矩阵分别为

以上3个判断矩阵也都是一致性判断矩阵，归一化的3个权重向量为

［1／19　9／19　1／19　8／19］T

［9／12　1／12　1／12　1／12］T和

［8／26　9／26　1／26　8／26］T

同样按照传统AHP中的算术加权平均法，张三、李四、王五和赵六4个人的排序权重为

张三：

李四：

王五：

赵六：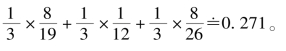

因此，当考虑张三、李四、王五和赵六4个人在总成绩上的排名时，排序为

张三≻李四≻赵六≻王五

可以观察到逆序现象发生了：在没有加入赵六的成绩之前，李四≻张三；在加入赵六的成绩之后，张三≻李四，即在添加赵六成绩的前后，张三和李四的排序发生了逆转！

AHP中的这种逆序现象，应该是很严重的一个现象和问题。试想一下，北京某高中同年级有6个毕业班，张三、李四在一个班，高考成绩出来后，如果用AHP对学生成绩排名，这种逆序现象的表现就是，班里排名张三比李四强，校里排名李四可能比张三强，年级排名可能张三又比李四强，区里排名可能又是一个样，市里排名可能换了另一个！相信这种现象是学生、家长、学校、社会都不能接受的。当然，高考成绩排名并不采用AHP。但AHP普遍地出现在国内的运筹、管理与决策的教科书中，书中却绝口不提AHP的逆序现象或国际学界对AHP的其他争议。每年无数的本科生、研究生在不知道逆序现象的情况下学了这个方法，然后在学位论文或毕业后工作中应用这个方法。想想每年那么多管理类的硕士、博士要开题、做论文，为什么在教科书里不向学生介绍些学界前沿、学术史上有争议且未解决的问题呢？相反，学生在不知道这些学术史上有争议且未解决的问题的情况下，学了、用了、用着这些方法。据笔者在国内高校商学院的从教经历，每年有1／3左右的管理类专业硕士学位论文用到或至少提到AHP。