初中数学教学：活化与生活融合

（一）数学情境要具有启发性，启发学生思维

有效的数学情境应具有启发性，有利于学生主动观察、交流讨论、推理、积极思考。数学是思维的体操，数学建构主义观点下数学学习的本质是数学思维构造，思维构造是需要学习者的智力参与的。因此，在初中数学教学中，如果情境的选择是合理的话，则有助于启发学生的思维，让学生充分感受数学，主动探究和运用数学，而在教学层面上有利于教师完成教学目标。正如弗赖登塔尔所说：“学生自己发明数学就会学得更好。”

案例：“圆的基本性质”第一课时的教学片段。

情境引入：现有一个小立柱，请问全班同学如何站，到小立柱的距离相等？请设计你的方案。

首先让学生自己设计方案，引出圆的定义，然后让学生自己根据设计的方案，总结圆的定义，最后再探究圆的其他概念及基本性质。

课例片段赏析：本节课中，教师通过引导，抛出问题，让学生自己设计方案，引出圆的定义及圆的基本性质。此节课的情境引入科学地引导学生探讨知识，启发学生思考问题，设计方案，让学生感受知识的发生、发展和应用，符合初中学生的知识建构，以及学生的年龄、心理特征。

（二）数学情境要具有科学性，符合学科特点

有效的数学情境必须是科学的、实际的，符合学科特点，实事求是，遵循事物客观发展规律，而不是无中生有、肆意编造的情境。在数学教学中，只有真实而科学的情境，才能取得良好的教学效果。如果只是单纯地追求教学情境的新颖丰富、多彩绚丽，而不注重情境的科学性，最终会得到适得其反的效果。

案例：三角函数——正切（第一课时）。

1.教学目标

知识与技能：理解正切、坡度的概念，并能运用正切、坡度解决简单的问题。

过程与方法：探究如何描述坡面的倾斜程度及正切的关系，渗透数形结合的思想，培养学生观察、分析、讨论、抽象概括能力，经历从特殊到一般的过程。

情感态度与价值观：经历正切概念的探索过程，体会建模思想的重要性，培养学生的符号意识，体会正切在生活中的应用。

2.教学重难点

教学重点：探究正切函数的定义。

教学难点：探究正切函数的定义及与坡度的联系。

3.教学过程

（1）创设情境，引入新课

在生活中人们爬坡是经常性的，那大家有没有想过，怎样描述坡面的坡度（倾斜程度）呢？下面我们一起来探究。

（多媒体展示生活中遇到的坡路，再利用几何画板抽象成直角三角形，用数据科学地比较坡路的倾斜程度）

如图3-1所示，有两个直角三角形（两个坡面），直角边AB与ED表示水平面，斜边AC与EF分别对应两个不同的坡面，问AC与EF哪个更陡？你又是怎样判断的？

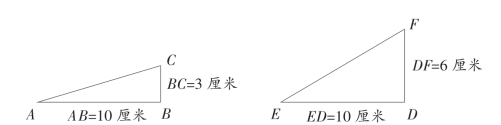
图3-1　三角形

如图3-2所示，坡面AC和EF哪个更陡？你又是怎样判断的？

图3-2　三角形

如图3-3所示，坡面AC和EF哪个更陡？你又是怎样判断的？

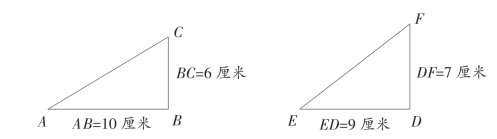
图3-3　三角形

设计意图：通过抽象实际问题，让学生观察、比较、讨论，探究坡度除了与坡角有关外，还与铅直高度和水平宽度有关。

学生讨论，探究坡度的概念。

教师引导学生，概括坡度的概念。

（2）探究新知

教师：坡面的铅直高度h与水平宽度l的比i=称为坡度（或坡比）。

教师：如图3-4所示，一条斜坡路面，其坡角一定了，那么它坡面上的任意一段路面的坡度是不是也一定？

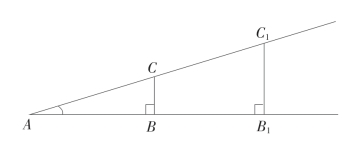
图3-4　斜坡

设计意图：借助几何画板，进行图形的动画演示和验证，揭示了∠A的对边与∠A的邻边的比和∠A这两个变量之间存在一一对应的函数关系，科学地解释了正切的概念。

学生讨论在直角三角形中，角的对边与角的邻边比值的关系。

教师引导学生探究正切函数的定义。

在Rt△ABC中，如果锐角A确定，那么∠A的对边与邻边的比随之确定，这个比叫作∠A的正切，记作tanA或tan∠BAC。

（3）回归情境

如何描述坡面的倾斜程度呢？介绍坡度的概念，记住关系式：i=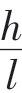=tan∠A。

在日常生活中，刻画倾斜程度常常用坡角（或倾斜角）的大小来表达，但是在大量实际问题中，坡角是不可测量的，所以可以用坡角的正切描述坡面的坡度（倾斜程度）。可见，坡度（i=tan∠A）越大，坡角就越大，坡面也越陡。

设计意图：体会数学源于生活并运用于生活，同时解决情境引入中提出的问题——坡度和坡角都可以用来判别坡面的倾斜程度。

课例片段赏析：本节课中，通过真实的生活实际问题作为情境引入，抽象成数学问题，科学引导学生探讨知识，让学生感受知识的发生、发展和应用，符合初中学生的知识建构规律和学生的年龄、心理特征，对教材的处理恰当，以学生为主体，教师组织与引导学生进行课堂展示。

（三）数学情境要有发展应用性，符合实际

有效的情境是真实可靠的，是符合实际生活的。建构主义的学习观认为，学习发生的最佳情境应是，在现实世界的具体情境中，学习才会变得有效。在这样的真实情境中，学习者知道数学知识源于生活，并服务于生活，达到学以致用的目的。

案例：“反比例函数”的教学片段。(www.xing528.com)

教学内容：反比例函数（第一课时）。

1.教学目标

知识与技能：理解反比例函数的概念，会解决简单的反比例函数问题。

过程与方法：探究反比例函数的概念，渗透类比数学思想，培养学生观察、分析、抽象等能力，经历从特殊到一般的过程。

情感态度与价值观：在抽象概括反比例函数过程中，让学生体验数学是源于生活，并服务于生活，与实际生活联系密切。

2.教学重难点

教学重点：理解反比例函数的概念。

教学难点：理解反比例函数的概念，能够区别正比例函数与反比例函数。

3.教学过程

活动1：

教师：课余时间大家和自己的同学逛超市买过文具吧？下面，老师带着你们逛一逛超市。同时，我们边逛边思考下列问题。

（多媒体展示超市购物时的图片）

问题1：若有一种文具单价为x元，用10元钱买这种文具能够买文具y，问y与x满足怎样的关系式呢？

问题2：若一本笔记本5元，如果买a本，所花的钱数y应如何表示？

问题3：其中有个同学已经花了30元，还想买1.5元/支的笔芯n支，则他总共要付的钱y与n的关系如何表示？

问题4：同学们逛完超市后，又打算逛一逛图书城，已知此超市距离图书城大约有1000米，则同学们到图书城所用时间t与平均速度v之间的关系如何？

问题5：观察上述几个生活中的例子所列的表达式，即y=5a，y=30+1.5n，思考以下问题：这里有我们熟悉的函数吗？每个表达式中有几个变量？这些变量之间有联系吗？能具体说一说它们之间的联系吗？

活动2：

问题6：若长方形的面积为216m2，其长和宽分别为x，y，问y与x之间的表达式。

问题7：某鞋厂计划生产一批鞋，其计划用t天，生产6000双，问平均每天的生产量y（双）与生产时间t（天）之间的函数表达式。

课例片段赏析：这节课情境的创设的有效性优，通过两个活动，而且都是从学生实际生活出发，简单易理解，不仅可以激发学生学习数学兴趣，而且还促进教学目标的实现。因此，对于情境的创设，教师在生活中要明察秋毫，观察生活中的数学，确保情境的真实性，符合数学学科特点，同时还要从学生已有的经验出发，让学生在知识上产生冲动，有学习新知的冲动，抽象概括反比例函数的概念，突出数学源于生活的理念。

（四）数学情境要具有可操作性，便于教学实施

有效的数学情境要具有可操作性，便于教学实施、学生理解与操作，能让学生参与活动中。数学建构主义学习特征之一是“自主活动”，强调以学生自主活动为基础，以智力参与为前提，完成个人体验。因此，情境要体现以学生为主体，便于学生操作和实施，要求学生“做中学数学”。

案例：“黄金分割比例”一课。

1.教学目标

知识与技能：理解黄金分割的定义，会解决黄金分割的简单问题。

过程与方法：经历黄金分割定义的探究过程，渗透数形结合的数学思想方法，培养学生观察、分析、抽象等能力。

情感态度与价值观：经历黄金分割定义的探究过程，感受数学之美及数学在生活中的应用。

2.教学重难点

教学重点：理解黄金分割的定义。

教学难点：黄金分割点的位置探究及黄金分割数。

3.教学过程

（1）创设情境，引入新课

活动1：

教师：请十位同学上来，其中九位同学先后分别在讲台摆放九朵大小、颜色基本一样的玫瑰花，其中一位同学将它们摆放的玫瑰花拍一张照片，最后教师也摆放一朵一样的玫瑰花在讲台上的黄金分割点上，也拍张照片，然后用多媒体展示各自摆放的照片，比较哪张照片最好看。请大家观察、比较、讨论后，评出结果，并说明理由。也就是为什么在同样的条件下，这一张看起来更立体好看？为什么教师摆放的拍出来的照片效果更好呢？

学生积极参与讨论。

设计意图：同学们积极参与，对拍照片、选照片非常感兴趣，在最后教师抛出一个问题，再度调动学生的热情，使学生更加想参与课堂中。但是，课堂的掌控度不宜控制，新知过于抽象，学生不能够很好地解释出现的这种结果，发现新知。而教师要解释现象的原因，讲授新知。

（2）探究新知

黄金分割点的定义：在线段AB上，点C把线段AB分成线段AC和BC，若AC是AB和BC的比例中项，那么称线段AB被点C黄金分割，点C叫作线段AB的黄金分割点，如图3-5所示。

图3-5　黄金分割点

活动2：

教师：请十位同学上来，其中九位同学先后分别在讲台每人摆放两朵大小、颜色基本一样的玫瑰花，其中一位同学将它们摆放的玫瑰花，各拍张照片，然后用多媒体展示各自摆放的照片，比较哪张照片最好看。请大家观察、比较、讨论后，评出结果，并说明理由。也就是为什么在同样的条件下，这一张看起来更立体好看？

设计意图：通过再一次排放花朵，来探究一条线段上有两个黄金分割点，这次教师不参与活动，让学生自己发现、观察、比较、讨论，得出结果，培养学生的类比能力。

课例片段赏析：此节课中同学们玩得很热闹，由摆放花朵到拍照比较，学生的参与度之高，而且情境设计便于教学实施、学生操作，突出了学生在做中学数学的理念。教学中的情境营造了良好的认知环境，促使学生产生认知冲突，激发学生感受美、设计美的欲望，同时突出数学源于生活，并服务于生活，从而可知有效的情境应是具有可操作性的，是便于教学实施的。

（五）数学情境要符合学生当前的认知水平

一个有效的情境必须符合学生认知发展规律，因为知识的建构是在已有的知识经验上建构新知。正如心理学鼻祖皮亚杰认为初中学生的心理发展具有共同性和差异性，虽然在年龄阶段上处于形式运算阶段，但真正达到形式运算阶段的人只是少数的。所以，这要求数学教师在进行教学时，不仅要考虑学生的共同点，还要考虑学生的差异性及心理发展的程度。

（六）数学情境要具有目标指引性，突出教学重点

有效的情境要突出重点，具有目标指引性。建构主义的学习观认为，目标是定向的，因为只有学习者清晰地意识到自己的学习目标，形成与获得所希望的成功相应的预期，学习才能是成功的。所以，一个有效的情境一定要是目标明确、重点突出，这样才可以合理地被应用。