生活化与初中数学教学的融合：实际问题与二次函数案例

（一）设计理念

通过层次问题的设计，让学生轻松地获得知识；通过模拟现实的生活场景，让学生在愉快的氛围下感受数学在现实生活中的魅力。

（二）学习目标

1.知识目标

初步让学生学会用二次函数知识解决实际问题，探究实际问题与二次函数的关系。

2.能力目标

通过研究生活中的实际问题，让学生体会建立数学模型的思想；通过学习和探究现实数学问题，渗透转化及分类的数学思想方法。

3.情感目标

通过实际问题，体验数学在生活实际中的广泛运用，发展数学思维，在经历和体验数学发现的过程中，让学生亲自体会到数学的价值，提高思维品质，激发学生学习热情。

（三）教学重难点及方法与教具准备

1.教学重点

如何将实际问题转化为二次函数的问题，用二次函数的知识解决实际问题。

2.教学难点

将实际问题转化为二次函数的问题，建立二次函数数学模型，解决问题。

3.教学方法

引导、启发式教学，学生自学，生生互动、师生互动，学生自主学习，合作探索。

4.教具准备

多媒体课件、实物投影仪。

（四）教学过程

1.创设情境，激发学生学习兴趣，引入新课

教师：在讲课之前，我对咱班的学生先做一个小小的调查。你们的父母中有做生意的举手示意一下（教师清点人数），务工的举手示意一下。好的，谢谢!那么，我想问一下，务工也好，做生意也好，目的都是干什么？

学生：挣钱。

教师：挣钱，一是靠我们辛勤的劳动，二是靠我们的智慧（科学文化知识）。我们班李强的爸爸文化程度不高，他有一个问题想请大家帮帮忙（引出例1）。

2.提出问题，分析问题，解决问题

例1：咱们班李强家开了一个商店，一种商品按照每件60元每周可卖出300件。经过调查市场，该商品如果单件涨价1元，那么每星期要少卖出10件；如果单件降价1元，那么每星期可多卖出20件。已知该商品的进价为每件40元，试问单件定价多少时该商品的利润最大？

分析：怎么确定函数关系式？有哪些相等关系式？变量x是否有范围？

解：调整价格包括涨价和降价两种情况。

（1）设每件涨价x元，则每件的利润为（60+x-40）元，可卖的商品的件数为（300-10x），此时每星期商品的利润为y元，于是有y=（60+x-40）（300-10x）=-10x2+100x+6000=-10（x-5）2+6250，其中0≤x≤30。

∴当x=5时，y最大=6250元。

所以，在涨价的情况下，每件涨5元即定价为65元/件时，利润最大是6250元。

（2）设每件降价x元，则每件的利润为（60-x-40）元，可卖的商品件数为（300+20x），此时每星期商品的利润为y元，于是有y=（60-x-40）（300+20x）=-20x2+100x+6000=-20（x-2.5）2+6125，其中0≤x≤20。

∴当x=2.5时，y最大=6125元。

所以，在降价的情况下，每件降价2.5元即定价为57.5元/件时，利润最大是6125元。

综合（1）（2）可知，商品的定价为65元时才能使利润最大。

由此题可知，做生意也是有很大学问的。只靠“勤劳”未必能挣更多的钱，还是应多学习科学文化知识，要珍惜咱们学习的大好时机，将来挣更多的钱，过上更美好的生活。要记住：不好好学习，就是一个最大的浪费者。

等卖了货之后，清点了靠自己合法经营赚来最多的钱高高兴兴地锁上门正准备回家时，突然变天要下大雨，李强的爸爸在回家的路上要路过一座危险的拱桥（引出例2）。

例2：图1-13是一个抛物线形的拱桥，正常时拱桥离水面2米，水面宽4米，当下大雨时，水面以每小时0.5米的速度上涨，当桥下的水面宽为2米时，桥就有被冲垮的可能。李强的爸爸下午3点从商店出发，此时天正在下大雨，问他最迟在下午几点之前要通过这座拱桥？

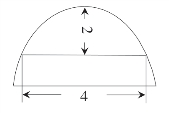
图1-13　拱桥纵截面

分析：用转化的思想引导学生分析怎样去解决问题。要求时间，有速度转化为求距离；要求距离，转化为建立二次函数数学模型，解决了常水位与警戒线水位纵坐标的差。

解：以抛物线的顶点为原点建立如图1-14所示的坐标系。(www.xing528.com)

由题意可知，A（-2，-2），B（2，-2）。

设抛物线的解析式为y=ax2，

∴-2=a×22，

∴a=

图1-14　拱桥纵截面抛物线图

这个二次函数的解析式为

当x=1时，

∴OD=

则CD=OC-OD=

所以水面宽由4米上涨到水面宽2米时，水面上涨的高度为1.5米，此时需时间为1.5÷0.5=3小时。

故小红的爸爸务必在下午6点之前经过这座拱桥。

此题鼓励学生用多种建模的思想去解决，然后让学生上台去展示自己的成果，并从中总结出“先想后算，多想少算，反思巧算”。

由于李强的爸爸急忙赶路，回到家已经很累，所以要吃饭，以此引出锅的问题（例3）。

例3：李强的爸爸为了赶路，到家之后已经累得精疲力竭，正好李强已经放学回到家中，慌忙去为爸爸做点饭吃。此时，正在上九年级的李强发现自己家铁锅的轴截面也呈抛物线形。这时，锅中的水最深处是5cm，已知锅口的半径是20cm，锅的高度是10cm，如图1-15所示，请同学们帮助正在做饭的李强算一算锅中水面的面积是多少？

图1-15　铁锅

利用上题的经验来解决本题起到一个巩固的作用。

解：如图1-16所示，以抛物线的顶点为原点建立平面直角坐标系，由此可知A（-20，10），B（20，10）。

设抛物线的解析式为y=ax2，

于是有10=400a，

∴a=

图1-16　铁锅轴截面抛物线图

∴抛物线的解析式为

当y=5时，

∴此时水面的半径为

则锅中水面的面积是200πcm2。

饭吃完了，本节课也即将结束，茶余饭后我们来谈一谈本节课的收获。

3.运用新知，拓展训练

小试牛刀：某旅行社组团去外地旅游，30人起组团，每人单价800元，旅行社对超过30人的团给予优惠，即旅行团每增加一人，每人的单价就降低10元，请你帮助算一下，当一个旅行团的人数是多少时，旅行社可以获得最大的营业额？

4.归纳与总结

通过本节课的学习，你有什么收获？

（1）二次函数与我们的现实生活密不可分，生活中缺的不是数学，而是缺少发现数学的眼睛。

（2）知道对于生活中的实际问题怎样去建立数学模型。

（3）运用函数知识解决实际问题，要考虑自变量的取值范围，要检验解的合理性。

（4）情感、态度方面的收获。

5.布置作业

必做题：课后习题第1，2题。

选做题：第3题。