看待任何一个问题都不应该只看到它们的表象,那么怎么透过问题的表面去找到问题的本质呢?数学教学中所需要的具有典型代表性的教学素材,其实现实的世界已经提供给教师了。怎样激活这些素材,不断挖掘这些素材背后所隐含的数学知识,是数学教学生活化的关键所在。深入学习数学知识的过程就是,将数学知识不断地从生活实践中抽象出来进行分析,再将得到的结论应用到生活实际中去。所以,初中数学生活化的教学除了注重选择生活化的教学素材外,也要注重教学内容落实的生活化。为此,数学生活化教学必须使学生具有自主学习、不断学习的主体意识,在不断地抽象概括、应用知识、再抽象概括、再应用知识中促使他们更快地获得数学的核心素养:数学抽象、直观想象、数学建模和数学运算。
(一)函数类
函数一直是困扰学生的一座大山,而且函数与自变量之间的一一对应关系是学生从未接触过的新型关系。一次函数的讲解需要有足够多的实例来帮学生巩固一次函数的建立过程。
例7:教师展示例子,请同学们思考下列问题中,两变量间是函数关系吗?若是,请写出函数关系式。
(1)在20—25℃时蟋蟀每分钟鸣叫次数C与温度t(℃)有关,即C的值约是t的7倍与35的差。
函数关系式:C=7t-35(20≤t≤25)。
(2)一种计算成年人标准体重G(单位:kg)的方法是,以厘米为单位量出身高值h,再减常数105,所得差是G的值。
函数关系式:G=h-105。
(3)某城市的市内电话的月收费额y(单位:元)包括月租费22元和拨打电话xmin的计时费(按0.1元/min收取)。
函数关系式:y=0.1x+22。
(4)某登山队大本营所在地的气温为5℃,海拔每升高1km气温下降6℃,登山队员由大本营向上登高xkm时,他们所在地的气温是y℃,试写出y与x之间的关系式。
函数关系式:y=-6x+5。
形成概念:C=7t-35(20≤t≤25),G=h-105,y=0.1x+22,y=-6x+5。
通过四个问题得到四个函数,引导学生在分化和类化各式的特征中发现一类不同于正比例函数的函数,训练学生的数学建模与数学抽象思维能力,进一步引出研究一次函数的必要性,并为类比、抽象、概括出一次函数的定义做铺垫。同时,让学生在思考、对比、分析、类比、迁移中,自己构建一次函数的概念模型。
(二)方程或不等式类
在方程的学习中,正确找出问题中的未知量和其中的等量关系是学好一元一次方程也是学好方程类问题的关键。
例8:根据问题,设未知数并列出方程。
爷爷想要围一个周长为20米的正方形篱笆,养鸡和兔子,这个篱笆的边长为多少米?
相等关系:篱笆边长的4倍等于20。
解:设篱笆的边长为x米,则有4x=20。
教师引导学生根据以上例题解决的过程进行总结,并得出根据实际问题列方程的一般步骤,如图1-5所示。

图1-5 根据实际问题列方程的一般步骤
学生活动:积极参与问题的讲解,思考列方程处理实际问题的一般步骤,以及为何经历以上步骤。
本节课的一条主线是围绕处理贴近生活的问题进行的。这样,不仅能让学生体会到数学是为应用而生的,而且可以提高他们的学习兴趣,同时提高他们分析、思考、总结的能力。
本环节教师讲解的重点是学生如何把文字相等关系转化成数学式子。
教师在利用有趣又实用的例子调动了学生的积极性后,不能轻易舍弃这个例子进入接下来的学习,而是延续这个例子,对其进行深入分析,进而导出接下来要分析的数学问题。
不等式问题与一元一次方程对比,主要难在不等号的方向和是否包含等号。符号的种类和相关性质更多,学生如何去正确掌握这些符号语言和不等式的性质,下例展示了一个很好的方法。
例9:同学们思考并讨论以下问题:以共享单车为例,若两家品牌在北京都多投放相同数量的单车,两家投放量会有什么样的关系?
此时,教师加以引导:“=”没有方向性,意味着两边的数量关系是相等的,所得结果仍是等式,而不等号“>、<、≥、≤”具有方向性,对比两者的不同,接下来应该重点研究不等号在方向上的变化。
假如两家品牌都多投放1万辆,则小黄车为150+1(万辆),摩拜为30+1(万辆),可以看出151>31。
假如两家都多投放2万辆,则小黄车为150+2(万辆),摩拜为30+2(万辆),可以看出152>32。
若两边加上的是相同的量,可以用相同的字母a表示,就能得到150+a>30+a。
之后,以共享单车为例,可以依次得到不等式的其他性质。通过多媒体以不同的方式呈现,题型多样,生动活泼,能激发学生的探究愿望,满足了学生多样化的学习需求。
在此例中,教师并没有像传统教学那样简单罗列出不等式的几项基本性质,而是把共享单车中的一组问题让学生自己分析,而学生通过观察、猜想、讨论和验证得出结论。由简单的思考开始,逐步加深、深化,不断地激发学生作为学习主体的主动性,每一个学生都在动脑思考、动手练习。这为接下来的难点学习打好了基础,而且贮备了充足的动力。这充分地体现了建构主义的自主、自发的理念。(https://www.xing528.com)
在上述的深入学习过程中,不仅使学生对生活中的不等式实例有了更深的认识,对不等式的性质有了更加深入的理解,而且又发展了学生的自主探究能力和自学能力。
(三)几何、三角类
讲解相似图形时,先让学生简单了解相似的概念,然后根据相似的特点去寻找自己生活中都有哪些相似图形,并将其抽象成数学中的相似多边形。这样,不仅可以提高学生的参与性和积极性,而且还可以感受相似图形离自己生活很近。
例10:把生活中的相似形抽象成相似多边形,如图1-6所示。
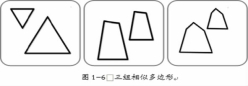
图1-6 三组相似多边形
尝试:给抽象出的三组几何图形命名。
列举:生活中的相似多边形。
练习:判断图1-7中各组图形是否相似。

图1-7 三组不相似图形
学生在生活中找到的相似图形有大小国旗、三角板、地图、照片。图1-7中前两组图形不相似,因为仅仅横向或纵向拉伸压缩,形状发生了改变。第三组图形中不相似,为什么呢?因为利用几何画板把外边缘的矩形的长和宽按相同比例缩小后,发现不能与内边缘矩形重合。
教师利用几何画板,将数学知识与生活中的例子结合起来,这样创设出来的生活情境不仅能让学生主动参与进来,还可以帮助学生更快、更好地学习抽象的数学概念。
三角类问题主要有三角形与全等三角形,学生在小学时期接触过此类知识。初中将小学中的这类问题深化,教师不能再让学生简单地去量一量、测一测,而是需要通过更新颖的方法让学生学习。
例11:学生动手操作,剪出等腰三角形,如图1-8所示,并通过观察,在教师的引导下对等腰三角形的性质进行大胆的猜想,得出结论。
问题:将自己手中的等腰三角形纸片对折,观察重合的线段和角,你有什么发现?
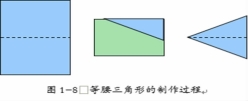
图1-8 等腰三角形的制作过程
学生:
(1)等腰三角形的两底角相等。
(2)折痕是等腰三角形顶角的平分线。
(3)折痕是等腰三角形的中线。
(4)折痕是等腰三角形的高。
(5)折痕分得的两个三角形全等。
学生借助自己亲手制作的学具,展开探究活动,通过观察、思考、猜想、交流,逐步体会研究几何图形的基本思路,通过直观想象、大胆猜想,在探究过程中积累数学学习的经验。这体现了由特殊到一般的过程。
(四)统计、概率类
在教学过程中,教师如果以学生在学校真实发生过的事情为例,更容易调动学生的注意力,因为这是与学生的切身利益息息相关的。
例12:问题一:学校组织的演讲比赛中,评委们按演讲效果占10%、演讲能力占40%、演讲内容占50%计算参赛选手的综合成绩(百分制)。A与B两位选手的成绩如表1-2所示,试比较谁的成绩更好。
表1-2 演讲比赛成绩

问题二:某校八年级一次数学考试中,一班的平均分是90分,二班的平均分是95分,你能求出这两个班的数学平均分吗?
师生活动:教师先让学生思考,再倾听学生的想法,然后再给出人数,只列式不计算,最后总结此题中人数是“权”,进而总结出“权”的三种形式——比例、百分数、频数。
这是一道十分贴近学生生活又容易做错的题目,设计这道“缺少条件”的题目,其目的是让学生在“错”中再一次顿悟到“权”的作用。生活化教学将生活中的统计类问题和加权平均数有效地联系起来,让学生再次深刻体会“权”对平均数的影响,让学生体会“权”的表示形式。
直观性是能促进学生的抽象思维发展的。在以上的例题中,广泛使用的符号的直观性(图形、图像、图式、图表)把所要研究的事实、现象和过程,同其他的性质分开了,并表现为一种更纯粹的数学形式。
学生从生活中抽象出数学问题,然后用数学的基本思想方法和技能解决寻找到的问题,从生活实例中感悟到数学思想和方法。学生在初中数学学习到的思想方法,如分类讨论、将难的转化为简单的、用熟悉的代换不熟悉的等,在生活中应用很广泛。细心观察会发现,生活中很多解决问题的思考方式和解决方案其中隐藏的思想与方法,其实就是中学生在数学中学习到的思想和方法。所以,教师在进一步引导学生深入探究知识点时,不直接将解题方法告诉学生,而是先引入学生在平时生活中解决问题的办法,为数学的思想方法做铺垫,这样学生更容易去理解,也更容易将学习到的数学知识应用到自己的生活中去。其实,这个过程就是学生先去收集生活中的例子,然后根据生活化素材构建“数学模型”,这样学生就会感觉到数学“鲜活”起来,而不仅仅只是数学课本中的一个个枯燥的公式和定理。这样,对学生今后的生活和学习也会产生有利影响。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




