高中数学思维方法：运用分类讨论解决问题的三个原则

（一）科学分类，准确讨论

分类标准的确立：每一次分类都要做到标准明确，要执行一个标准，任何两类不相容（交集为空集），所有类别的并集为问题的全部，这样就可以保证不重复、不遗漏、最简洁；另外，还要注意既能方便分类又有利于最后整合.所以分类标准的制定和使用，对获得问题的思路有重要意义.

分类标准既不能提前预设，也不能一蹴而就，伴随着我们对问题探究的深入，对问题的全方位信息有了一个整体全面的认识，对获得结论的各种障碍有了比较确切的理解，分类标准也就呼之欲出了.它往往是“被迫”做出的.只有这样分类，问题才能自然把控、分头推进.

使问题的研究能够得以继续，就是分类讨论最好的理由.

例10 数列{an}满足a1，nan+1=（n+1）an+n（n+1），n∈N*.

（1）证明：数列是等差数列；

（2）设bn=（-1）nan，求数列{bn}的前n项和Sn.

探究：（1）因为nan+1=（n+1）an+n（n+1），n∈N*.

考虑到结论的特征，应该尝试两边同时除以n（n+1）

所以数列是等差数列，首项为1，公差为1，

所以，所以an=n2.

（2）bn=（-1）nn2，这是一个摆动数列，可以考虑“配对求和”；当然，还是离不开分类讨论，因为前n项未必刚好成对.

若n为偶数，则Sn=-12+22-32+42+…-（n-1）2+n2，

每一对都可以利用平方差公式寻求一种积极的变化.

若n为奇数，则Sn=-12+22-32+42+…-（n-2）2+（n-1）2-n2，

最后一项不能成对，其他的和刚才完全相同.

综上所述，当n为偶数时，当n为奇数时

说明：配对求和结合分类讨论，使得问题转化成我们熟悉的模式.对一些有特点的数列，在求和的时候，往往可以结合问题的具体特征，对项数n的奇偶性进行分类讨论，进而将问题标准化.其实，少年高斯当年对1+2+3+…+100的计算，就是配对求和，把加法升级为乘法.试想一下，1+2+3+…+n的求和完全可以在分类讨论的基础上，采用分类讨论整合的方法，和课本上的倒序相加法等效，但是前者更容易想到更和谐更自然.

例11 现有五种不同的颜料，要给四棱锥P-ABCD的五个表面涂色，规定：有公用边的两面不得同色，问：最多有多少种涂色方案？

探究：如图所示，完成涂色成功需要5步.

例11图

第一步：给下底面涂色，有5种选择.

第二步：给左侧面涂色，不能与下底面同色，有4种选择.

第三步：给后侧面涂色，不能与下底面左侧面同色，有3种选择.

第四步：给右侧面涂色，不能与下底面后侧面同色，有3种选择.

第五步：给前侧面涂色，不能与下底面左右侧面同色，有几种选择呢？问题出现了意外！

给前侧面涂色的时候，问题变得难以确定了，当左右两个侧面的颜色相同或者相异，涂色方法不一样了，而这就是分类讨论的标准.

第一类：若左右侧面同色，它们相当于一个面，此时我们可以分四步走，先下底面，再左右面，第三是前面，第四是后面：5×4×3×3=180种方法.

第二类：若左右侧面不同色，此时我们可以分五步走，先下底面（5种方法），再左面（4种方法），第三是右面（不与左面同色也不与下底面同色，只有3种方法），第四是前面（2种方法），第五是后面（2种方法）：5×4×3×2×2=240种方法.

所以，共有420种方法.

说明：需要分类讨论的问题，同样应该按照普通的数学问题去思考去探索.只有当我们发现问题元素不确定，或者问题条件中的不同元素对后续研究有着不同的影响的时候，我们才按照问题的确定性和对后续问题的影响性进行明确分类.明确的分类其实就是成功的一半.

本题还有另一种分类方案：按照使用颜色的多少来分类，如果使用5种颜色，就是5种元素在5个位置上的全排列：.如果使用4种颜色，那要么前后面同色，要么左右面同色，都是5个元素选取4个的排列：；如果使用3种颜色，则应该前后面同色且左右面同色，是5个元素选取3个的排列：.

下面的问题与此题类似，用刚才的方法试试呗！

将一个四棱锥P-ABCD的每个顶点染上一种颜色，并使同一条棱的两端点异色，如果只有5种颜色可使用，那么不同的染色方法的总数是_________.

本题答案是420.

分类的另一个标准是应该体现出化简的原则，也就是说分类之后问题变得简洁明晰了.

例12 （1）函数f（x）=|sinx|sinx+|cosx|cosx的值域是_________.

（2）函数y=sinx+cosx+|sinx-cosx|的最大值、最小值分别为_________.

探究：去掉绝对值符号就是一种化简，这当然需要根据实际情况进行分类讨论.

显然，该函数周期为2π.

时，y=sin2x+cos2x=1，

时，y=sin2x-cos2x=-cos2x∈[-1，1]，

时，y=-sin2x-cos2x=-1，

时，y=-sin2x+cos2x=cos2x∈[-1，1].

上述讨论刚好完成了一个周期.

综上所述，f（x）=|sinx|sinx+|cosx|cosx的值域为[-1，1].

根据三角函数的定义，sinx和cosx的大小关系的分界线为y=x.

显然，该函数周期为2π.

时，

时，

上述讨论刚好完成了一个周期.

综上，函数y=sinx+cosx+|sinx-cosx|的最大值、最小值分别为

说明：将分类讨论结合函数的周期性，成功地去掉了“烦人”的绝对值符号，把复杂的三角函数问题变成了标准性问题，问题得到了极大的简化.

（二）形成严谨的思维方式，强化分类讨论的自觉意识

数学研究是严谨可靠的，每一步推理运算都有严格的条件限制，超越了这个约束，问题往往会走向另外的方向.所以，明确算法算理，真正理解数学推理的本质，才能有效地防止以偏概全和一刀切的思维方式.

很多数学讨论问题，都有着比较明显的特征，比如含有字母系数的方程或者不等式、含有参数的函数表达式、某些不确定的制约关系.当它们出现的时候，我们就应该灵敏的闻见分类讨论的“味道”，不失时机地进行分类讨论和整合.

一定要形成分类讨论整合的自觉意识，现实情况是忽视讨论比不会讨论的现象更普遍.

例13 （1）一条直线过点（5，2），且在x轴、y轴上的截距相等，则这直线方程为（ ）.

A.x+y-7=0

B.2x-5y=0

C.x+y-7=0或2x-5y=0

D.x+y+7=0或2y-5x=0

（2）用一块长为3m，宽为2m的矩形木板紧靠墙角（墙角为直角）围出直三棱柱，则怎样能使得其容积最大？

（3）抛物线y=ax2的焦点坐标是_________.

（4）正方体木块有八个“角”（八个顶点），用一个平面将其截去一个“角”，则所得几何体有____个顶点.

（5）从0，1，2，3，4，5这6个数中任意取出三个不同的数字组成一个三位数，则恰好构成偶数的概率为_________（用数字回答）.

（6）长方体木块ABCD—A1B1C1D1中，AB=5，AD=4，AA1=3，一蚂蚁沿着木块表面由A点爬至C1点，求其最短路程，请说明最短路线共有多少条.

（7）a2+b2=5，b2+c2=13，c2+a2=10，则ab+bc+ca的最大值最小值分别为_________.

（8）在△ABC中，A=30°，BC=25，D是AB边上的一点，CD=2，△BCD的面积为4求，AC的长.

探究：（1）设该直线在x轴、y轴上的截距均为a，

则可设直线方程为，很容易求得a=7，所求方程为x+y-7=0.

这种方法将截距为零（直线过原点）这一种情况漏掉了.

当直线过原点时，可设其方程为y=kx，很容易得到直线方程为y=2 5 x，即2x-5y=0.

其实，当我们根据直线截距a设定直线方程的截距式时，严谨的思维方式就提醒我们，过原点的直线被我们忽略了.

（2）设直三棱柱的下底面所在直角三角形的一个锐角为A.

当高为2m时 容积

故A=45°时最大为4.5.

同理，高为3m时 容积V=3sin2A，最大为3，

故使三棱柱的高为2m，且木板与其中一面墙的夹角为45°时容积最大，为4.5.

矩形木板如何摆放（到底是矩形的高贴着地面还是矩形的宽贴着地面），两种情况都存在，容易被忽视而以偏概全.

（3）首先应该将抛物线方程标准化为，然后对系数a的符号进行分类讨论，最后经过整合.答案的表现形式是一样的，焦点坐标为

（4）若截面不经过原正方体的顶点，则剩下的几何体有10个顶点，8-1+3=10.如例13图①A所示.若截面只经过原正方体一个顶点，则剩下的几何体有9个顶点.8-1+2=9，如例13图①B所示.

若截面只经过原正方体两个顶点，则剩下的几何体有8个顶点，8-1+1=8，如例13图①C所示.

若截面经过原正方体三个顶点，则剩下的几何体有7个顶点，8-1=7，如例13图①D所示.

例13图①

所以结果为7，8，9，10四种情况.

以截面经过正方体的顶点个数分类求解，既是探究过程中的自然选择，也能确保分类标准不重复不遗漏，同时也有效地防止了以偏概全的简单化思维方式.

所有的三位数：特殊优先，先排百位有5种选择，剩下两个数位5×4，共有5×5×4=100个.

三位偶数：0，2，4排在个位上，但是它们对后续部分的影响是不同的，所以分类不可避免.

若0排个位，则百位有5种选择，十位有4种选择，共有5×4=20个；

若0不排在个位上，则2，4可以排在个位上，有2种选择，此时百位有4种选择，十位有4种选择（可以选0了），2×4×4=32.

所以，三位偶数共有52个，概率

在排列偶数的时候，0，2，4排在个位上对后续元素的选择和安排都是不同的，所以不能一概而论，分类不可避免了.分类讨论是一种自然和谐的选择，它是在解题过程当中“自发”的形成的.

本题中，如果研究其对立事件，可以必看分类讨论.

（6）如例13图②：

例13图②

长方体ABCD-A1B1C1D1的表面可如下图三种方法展开，分类讨论画出几何体的部分侧面展开图，利用直角三角形容易解得AC1的值.

路程可能如下.

方案1：将上底面和前侧面“摆平”，或者将下底面和后侧面“摆平”，答案为

方案2：将下底面和右侧面“摆平”，或者将上底面和左侧面“摆平”，答案为

方案3：将左侧面和后侧面“摆平”，或者将前侧面和右侧面“摆平”，答案为

所以，方案1为最佳方案，一共有两个路径.

如果这是个正方体，以上三种情形六个路径都是一样的，但是长方体问题便产生了偏移，答案发生了变化，需要我们依据具体情况进行具体分析.依据不同的路径，发现问题可以分为六种三类.这样一来，既简化了分类，又捕捉到了最佳选项.

（7）a2+b2=5，b2+c2=13，c2+a2=10，三个方程三个未知数，很容易得到a=±1，b=±2，c=±3.

求ab+bc+ca的最大值、最小值，需要对a，b，c的符号进行分类讨论：一共有8种4对组合方式，我们会得到以下4个不同的答案.

当a，b，c的符号全正时，答案为11；

当a，b，c的符号全负时，答案与上面完全一样；

当a，b，c的符号两正一负时，有三种情形，答案为1，-5，-7；

当a，b，c的符号两负一正时，也有三种情形，与上面刚好对应起来，答案完全一致.

综上所述，最终的最大值为11、最小值为-7.

由△BCD的面积为4可得，即

①当∠BCD为锐角时，

△BCD中，由余弦定理可得BD=4.

△BCD中，由正弦定理可得，即(www.xing528.com)

在△ABC中，由正弦定理可得，容易解得AC=4.

②当∠BCD为钝角时，

△BCD中，由余弦定理可得

△BCD中，由正弦定理可得

在△ABC中，由正弦定理可得

综上可得AC=4或

如例13图③，当由利用平方关系求解cos∠BCD的时候，严谨的思维方式应该提醒你：∠BCD很有可能为钝角.

例13图③

说明：当你的分类讨论成为数学研究的自觉意识的时候，你的严谨性、全面性、可靠性就提升到一个理想的高度了.

（三）有利有效性原则

在数学研究的过程中，应该实事求是地分析问题的条件和结论，具体问题具体分析，使得分类讨论有利于问题的发展；同时，能够有效地获得问题的结论，不要为讨论而讨论.

尽管分类讨论是有效的，但还是应该尽量避免分类讨论，尽量减少讨论的类别和级别（层次）.这样一来，我们的研究可以更加简捷高效，也可以不断提高数学的逻辑概括能力.

例14 （1）求函数的最大值和最小值.

（2）A为三角形的一个内角，曲线x2cos2A+y2sin2A=1上的点，都在圆x2+y2=4的内部，求角A的取值范围.

探究：（1）可以利用换元法去掉根号符号.

令x=sinθ，则

结果不甚理想，是否应该通过分类讨论去掉绝对值符号呢？能避免讨论吗？

考虑到原函数的定义域：-1≤x≤1，

所以只要在x=sinθ规定即可.

此时，显然其最大值最小值分别为

（2）由题意，曲线x2cos2A+y2sin2A=1只有三种可能：圆，焦点在x轴或者在y轴上的椭圆.

将曲线的方程标准化：

如图，你可以在圆的内部画出符合题意的椭圆（或者是圆）.你会发现，没有必要讨论其可能的三种情况，无论其表示什么样的椭圆，只要长半轴短半轴都小于题给圆的半径即可；如果曲线表示圆，也只需满足同样的关系即可.

例14图

要想研究三角形内角A的取值范围，最好得到其余弦的关系，因为余弦值与对应角度是一一对应的.

因为A为三角形内角，所以或

说明：该题说明三点.第一，很多分类的标准是在不得要领的时候，面对困难局面，靠认真观察分析才得到的；第二，在研究数学问题的时候，面对需要分类讨论的问题，坚持有利有效原则，对问题进行结构分析，很有可能避免分类讨论；第三，数形结合分类讨论与函数方程思想，往往事半功倍.

例15 设函数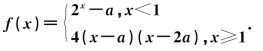

（1）若a=1，求f（x）的最小值；

（2）若f（x）恰有2个零点，求实数a的取值范围.

探究：（1）a=1时，

当x＜1时，f（x）的取值范围为（-1，1），此时f（x）无最小值；

当x≥1时，最小值为，即整个函数的最小值为-1.

（2）分段考虑函数f（x）的零点.

当f（x）位于x=1左侧时，y=2x-a单调递增，其取值范围为（-a，2-a），

故只有当即0＜a＜2时函数f（x）在直线x=1左侧存在零点.

当f（x）位于x=1右侧（含x=1）时，考虑y=4（x-a）（x-2a）的两个零点为x1=a，x2=2a，分别与x=1比较.

划分区间讨论，可得函数f（x）在x≥1时的零点个数：

当f（x）的两个零点有一个在x=1左侧，一个在x=1右侧时，

0＜a＜2且a＜1且2a≥1，也就是

当f（x）的两个零点都在x=1右侧时，则a≥1且0＜a＜2不成立，所以a≥2.

综上可得，当函数f（x）有两个零点时，a的取值范围是或a≥2.

说明：本题考查的数学思想既有数形结合更有分类讨论.这是一个分段函数，无论是求最小值还是研究零点个数，都是在两个分段区间上进行分类讨论.尤其是第二问，其实就是分析x=1的左右两侧各为函数整体贡献了几个零点.首先研究两个分段区间有零点的条件（左侧最多一个零点，右侧最多两个零点），看x=1的左侧产生几个零点是该题分类的唯一标准：若左侧一个零点，则右侧应该只有一个零点；若左侧没有零点则右侧，应该有两个零点.如此研究，在确保只有两个零点的情况下，锁定参数a的取值范围.这样的分类讨论简洁明了、有利有效；如果数形结合，可能更加直接有效.

例16 已知函数f（x）=（x+1）lnx-x+1.

（1）若xf'（x）≤x2+ax+1，求a的取值范围；

（2）证明：（x-1）f（x）≥0.

探究：

（1）xf'（x）≤x2+ax+1等价于lnx-x≤a，也就是a≥（lnx-x）max.

令g（x）=lnx-x，则；当0＜x＜1时，g'（x）＞0，g（x）为增函数；当x≥1时，g'（x）≤0，g（x）为减函数.x=1是g（x）的最大值点，g（x）≤g（1）=-1.

综上，a的取值范围是[-1，+∞）.

（2）采用分析法：要证明原结论，分两种情况，

只要证明x≥1时f（x）≥0，0＜x≤1时f（x）≤0.

导函数结果不甚理想，再来一次！

可得0＜x≤1，

所以在[1，+∞）上单调递增，在（0，1]上单调递减，

进而x=1时其最小值为1，

所以f'（x）恒为正数，即f（x）为增函数.

可以尝试着画出函数f（x）的图象，相信你马上就能找到感觉.

又由f（1）=0可得：

x≥1时f（x）≥0，原结论正确；

0＜x≤1时f（x）≤0，原结论也正确，

所以原结论正确.

说明：恒成立问题往往转化成函数的最大最小值问题；求字母系数的取值范围问题，往往将该字母系数与其他变量分离开来，从而转化成恒成立问题.

在第二问中，观察分析结论的结构特征，要证（x-1）f（x）≥0.其实，数形结合地联想一下，只要证明函数y=f（x）是一个增函数且其图象经过定点（1，0）即可.而这可以有目的地避开分类讨论，只不过我们在规范表述的时候，表面上采用了分类讨论的语言罢了.

例17 在平面直角坐标系中，方程=1（a，b是不相等的两个正数）所代表的曲线是（ ）.

A.四条直线

B.正方形

C.非正方形的长方形

D.非正方形的菱形

探究：分类讨论去掉绝对值符号是研究该题的基本方法.

当x+y≥0且x-y≥0时（第一、四象限角平分线之间）原方程可化为

在第一、四象限角平分线之间，它表示一条线段，分别与x+y=0和xy=0联立方程组可得交点坐标为D（b，-b），A（a，a）.

当x+y≥0且x-y＜0时（第一、二象限角平分线之间）原方程可化为

在第一、二象限角平分线之间，它表示一条线段，分别与x+y=0和xy=0联立方程组可得交点坐标为B（-b，b），A（a，a）.

当x+y＜0且x-y≥0时（第三、四象限角平分线之间）原方程可化为

在第三、四象限角平分线之间，它表示一条线段，分别与x+y=0和xy=0联立方程组可得交点坐标为C（-a，-a），D（b，-b）.

当x+y＜0且x-y＜0时（第二、三象限角平分线之间）原方程可化为

在第二、三象限角平分线之间，它表示一条线段，分别与x+y=0和xy=0联立方程组可得交点坐标为B（-b，b），C（-a，-a）.

画出图形可以发现四条线段的端点首尾相接，分别是A（a，a），B（-b，b），C（-a，-a），D（b，-b）.显然，四边形ABCD对角线互相平分（对角线的中点都是原点）且互相垂直，也就是四边形ABCD为菱形；又因为a≠b，也就是两条对角线长度不等，所以这是非正方形的菱形，选D.

说明：分四种情况进行分类讨论，看起来比较烦琐，但是分析和计算都是同构的，所以问题的难度并不是太大；而且，这样的分类讨论对问题的发展肯定是有效的，对获得问题的整体思路也是有利的.

另外不难发现，把x换成-x、把y换成-y方程都是不变的，所以本题的曲线关于坐标轴都是对称的.这样一来，问题还可以进一步简化.

例18 设f（x）是定义在区间（-∞，+∞）上以2为周期的函数，对k∈Z，用Ik表示区间（2k-1，2k+1]，已知当x∈I0时，f（x）=x2.

（1）求f（x）在Ik上的解析表达式；

（2）对已知的正整数k，求集合.

Mk={a|使方程f（x）=ax在Ik上有两个不等的实根}.

探究：（1）因为f（x）是以2为周期的函数，

所以2k也是f（x）的周期；

又因为当x∈Ik时，x-2k∈I0，

所以f（x）=f（x-2k）=（x-2k）2，

即对k∈Z，当x∈Ik时，f（x）=（x-2k）2.

（2）方法1：当x∈Ik时，利用（1）的结论可得方程：

(x-2k)2=ax.

因为目标元素为a，所以应该得到

进而

由题意可得，函数y=a与的图象有两个交点，

后者是一个传统的“对号函数”，定义域为（2k-1，2k+1].

最低点（2k，0），它的两个端点分别是：

如例18图①，容易得到

例18图①

故所求集合

方法2：当x∈Ik时，利用（1）的结论可得方程（x-2k）2=ax，整理得x2-（4k+a）x+4k2=0.

它的判别式是Δ=（4k+a）2-16k2=a（a+8k）.

数形结合一下：

令g（x）=（x-2k）2-ax（它的零点就是目标方程的根），g（x）=x2-（4k+a）x+4k2的图象，如例18图②所示.

可以发现，上述方程在区间Ik上恰有两个不相等的实根的充要条件是a满足：

例18图②

化简得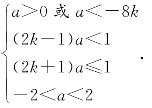

a是未知数，k为已知数，容易得到

故所求集合

说明：尽管这道题特别像一个分类讨论题，但是我们却巧妙地避开了，解答过程十分简练.

第一问里，我们没有盲目地对k进行讨论，而是把它看成一个已知数，利用函数的周期性，完成由已知区间向目标区间的转化，直接给出了x∈Ik时f（x）的通式.

同样，在第二问里面，我们也没有对a和k进行分类讨论，而是利用函数与方程思想进行数形结合.多种数学思想共同发力，问题得到圆满、简练的解决.

善于讨论、敢于讨论而又能巧妙地避免讨论，数学能力的成长永无止境！