高中数学研究中分类讨论思想的重要作用

分类讨论可以有效降低问题难度，明确解题思路，发现或者构造问题的简单解法.

分类讨论能把模糊的不确定的问题转化成清晰的确定的子问题.这个时候，我们可以更加清楚地发现问题内部元素之间的联系规律.

前面已经说过，如果分类标准清晰有效，那么就给我们增设了一个可以直接使用的条件.这个条件不仅仅会降低问题的难度，更会及早地洞察问题的结论.

例1 设0＜x＜1，a＞0且a≠1，比较|loga（1-x）|与|loga（1+x）|的大小.

探究：比较大小最常用的就是作差法，通过作差，对问题进行抵消约分合并同类项等化简措施.但是，该题的两个绝对值符号“十分顽固”，是最大的解题障碍，去掉绝对值符号本身就是一种化简.做到这点的主要方法就是针对绝对值内元素的符号分类讨论.

因为1+x＞1，0＜1-x＜1，所以当a＞1时，loga（1-x）＜0，loga（1+x）＞0，

|loga(1-x)|-|loga(1+x)|=-[loga(1-x)+loga(1+x)]

=-loga(1-x2).

因为a＞1，0＜1-x2＜1，

所以-loga（1-x2）＞0，

所以|loga（1-x）|＞|loga（1+x）|.

当0＜a＜1时，loga（1-x）＞0，loga（1+x）＜0.

|loga(1-x)|-|loga(1+x)|=loga(1-x2).

例1图

因为0＜a＜1，0＜1-x2＜1，

所以loga（1-x2）＞0，

所以|loga（1-x）|＞|loga（1+x）|.

综上所述，当0＜x＜1，a＞0，a≠1时，总有|loga（1-x）|＞|loga（1+x）|.

说明：分类讨论有效地解决了难缠的绝对值问题，使得对数的运算法则和对数函数的性质能够充分地发挥作用.在分类讨论整合的前提下，问题越来越简化，思路越来越清晰.

其实，该题也可以画出函数f（t）=|logat|的图象.如图所示，你会发现，无论a＞0还是0＜a＜1，其图象都是一样的：

在（0，1）上为减函数，图象下降很快；

在（1，+∞）上为增函数，增长缓慢.

所以，f（1-x）＞f（1+x），所以|loga（1-x）|＞|loga（1+x）|.

这是一个靠观察得到的结论，但没有得到严格的证明.上述的分类讨论过程，就是对我们观察结果的可靠性的证明.

例2 定点p（0，a）（a＞1）到曲线上的动点Q（x，y）的最小距离为5，求a的值.

探究：如图是的图象，可分两段.

例2图

当时，曲线方程为，显然|PQ|的最小值d1=a-1.

当或时，曲线方程为，即x2=2y+2，

所以y=a-1时，|PQ|的最小值

所以，当时，|PQ|的最小值为a-1此时1＜a≤4.

当时，|PQ|的最小值为，此时，a＞4，

即|PQ|的最小值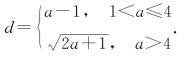

当1＜a≤4时，最小值a-1=5，所以a=6（舍去）.

当a＞4时，最小值，可以解得a=12.

综上所述，a=12.

说明：此题有两种分类讨论：

1.将曲线分为两段，求每一部分上的最小值后，再选择确定整体上的最小值.

2.在两个最小值的选择时，又进行了一次分类讨论，最后求解就用了这一次分类讨论的结果.

通过分类讨论，把一个不确定的整体性的难题分解成了几个单纯清晰的小问题，探究难度大大降低了，最后的整合完成了局部到整体的转化.

例3 某车间有10名工人，其中7人会车工，6人会钳工，现需选出6人完成一件工作，需要车工钳工各3人，问：有多少种派工方案？

探究：画出韦恩图容易看出；有3人全能，4人仅会车工，3人仅会钳工.

按照分步乘法计数原理，需要两个步骤：第一步选派车工，第二步选派钳工.

例3图

如果先考虑车工，因有7人会车工，故有C37种选法，但这些三人组合当中，到底有几个是全能的是不一定的，其对后面钳工的选择有完全不同的影响，因此需对全能工人进行分类.

方法1：选出的6人中不含全能工人；

选出的6人中含有一名全能工人；

选出的6人中含2名全能工人；

选出的6人中含有3名全能工人.

C34·C33+C34·C13·C23+C24·C13·C33+C23·C13·C34+C23·C14·C33+C23·C24·C23+C33+C34+C23·C14·C23+C23·C13·C24=309.

方法2：显然上述分类有些复杂，主要原因是选出的全能者，其去向还要二次讨论.

可以考虑按照选择车工的时候，到底包含了几个全能者来分类.

选择车工的时候，不选择全能者，那么钳工的选择范围便是6人；

选择车工的时候，选择了1名全能者，那么钳工的选择范围便是5人；

选择车工的时候，选择了2名全能者，那么钳工的选择范围便是4人；

选择车工的时候，选择了3名全能者，那么钳工的选择范围便是3人.

C34·C36+C24·C13·C35+C14·C23·C34+C33·C33=309.

说明：排列组合问题，主要是考查分类讨论的能力.解答这类题时，首先要确定好分类的对象.解这个题时，可以对全能工人进行分类，也可以对仅会钳工的人分类，还可以对仅会车工的人分类.不过，一般选择对象个数少的作为分类对象，这样讨论的类别相对就会少些.

分类之前，我们对问题的认识比较模糊；分类之后，由于内容比较单一，加上分类标准的指引，问题变得简单了，更容易获得解决方案.

分类最好一次搞定，不要牵扯到二级分类，分类之中再分类，这样太烦琐.

针对各类问题，分级进行，逐类讨论，逐步解决，不断获取阶段性结果，以循序渐进的形成对问题总体把控，最后进行归纳小结、综合得出结论，这是分类讨论思想的基本方式.

分类讨论是我们进行有效探究的主要方式.

万事开头难.对那些条件杂乱的问题，我们可能不能马上洞察其思路，但是它的一些子问题还是容易解决的.通过对子问题的不断突破，我们的思路可能会逐步明朗起来，问题的整体思路就会逐步显现出来.

例4 把不超过实数x的最大整数记作[x]，则函数f（x）=[x]称作取整函数，又叫作高斯函数.在[1，4]上任取x，则的概率为（ ）.

A. B. C. D.

探究：当我们思路不清的时候，可以对x的范围进行讨论，希望能从此打开思路.

当x∈[1，2）时，，此时

当x∈[2，3）时，，此时

当x∈[3，4）时，，此时[x]=3而

所以的概率为.

说明：分类讨论有时候不需要理由，它本身就是一个试探甚至是试错的过程.这也是一个审题的过程，在这个过程中，我们的思路慢慢被理顺了.

例5 三个不等实数的乘积为-8，将它们恰当排列后，可以成等差数列，也可以成等比数列，求这三个数.

探究：考虑到“三个不等实数的乘积为-8”，可设三个数按等比数列排列为

又

所以a=-2.

这三个数成为，-2，-2q（只要求出q即可，应该找到一个关于q的方程）.(www.xing528.com)

又因为它们成等差数列，本来这三个数的排列数有6种，但是当我们按部就班的精心讨论的时候，可以发现按等差中项的不同可简化为以下三类.

若为等差中项，则，解得q=1（舍去）或-2此时三个数为：1，-2，4；

若-2为等差中项，则，解得q=1（舍去）；

若2q为等差中项，则，解得q=1（舍去）或

此时，三个数为1，-2，4.

综上所述，这三个数为1，-2，4.

说明：因为条件之一为三个数的乘积为-8，所以我们采用等比数列的常规设置.

三个数成等差数列，其排序方式有六种之多，但是当你真正地去分类讨论的时候你会发现，对等差中项进行分类，问题还可以继续简化.

例6 有卡片9张，将0，1，2，3，4，5，6，7，8这9个数字分别写在每张卡片上，先现从中任取3张，组成一个三位数，若6可当9用，则可组成不同的三位数多少个？

探究：9个数排列成三位数：8×8×7=448.

其中，用到6的排列：

若6排在百位，则有8×7=56种；

若6排十位，则有7×7=49种；

若6排个位，则有7×7=49种.

因6可以当9用，故上述三种情况应该再加一遍，总和602.

另外，可以考虑间接法：假设9也参与排列，共有9×9×8=648种.

减去同时含6和9的，这需要讨论第三个数：

若第三个数为0，则有2×2×1=4个；

若第三个数不是0，则有7×3×2×1=42个.

最终答案为648-4-42=602.

说明：分类讨论可能在开始阶段有些迷茫，只透射到问题的一方面，但是，随着研究的深入，我们可以对问题有更明确的认识，甚至也能改正前面的某些不足或错误.

解答本题时，对于0，6，9三个数字的研究和安排是解题的关键.从简单开始，用过6的加倍计算，没有用过6的只算一次，所以是否用6就成了分类的标准；而在这些用过6的排列中，到底有几个，还要看0的“脸色”，所以是否用0又成了新的分类标准.

当分类讨论成为我们的解题习惯时，你的思考就容易走向正确的方向，而且严谨全面细致的风格会一直伴随着你，不犯错误、少走弯路就是一种大概率事件.

分类讨论可以让我们深刻理解数学问题的本质，真正形成数学能力.

在分类讨论和整合的过程中，无论是对审题，还是对思路的探究，还是对解题思想和研究成果的准确规范的表述，甚至是解题最后的整合过程，对我们的数学能力都是一次再夯实的过程.在这些过程中，我们对相关知识和方法的理解认识和把控，肯定会有一次次的提升.

例7 函数f（x）=-x2+|x-2|-1.（1）求证：该函数为非奇非偶；（2）求函数的最大值.

探究：（1）因为f（2）=-5，f（-2）=-1，

所以f（-x）=f（x）与f（-x）=-f（x）都不是恒成立，

所以f（x）既不是偶函数也不是奇函数.

（2）当x≥2时，f（x）=-x2+x-3，这是一个二次函数，对称轴为直线

则f（x）为[2，+∞）上的减函数，此时fmax（x）=f（2）=-5.

当x＜2时，f（x）=-x2-x+1，这也是二次函数，对称轴为直线x=

则f（x）在上为增函数，在上为减函数，

此时

综上，

说明：本题第一问考查分段函数的奇偶性，用反例分两种情况进行判断；第二问求函数的最值时，也是采用了分类讨论的方法，先通过分类讨论去掉绝对值符号，然后在每一种情况下分别求出函数的最大值，最后整合出问题的最终答案.

通过该问题，我们对函数奇偶性的否定（反例即可）和二次函数最大值的分类整合的认识，上升了一个档次.

例8 已知数列，数列{an}有最大项最小项吗？如果有，请说明分别是第几项；如果没有，请说明理由.

探究：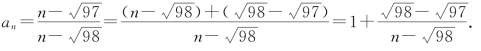

此时我们只要考查即可.

显然，当n=1，2，3，…，9时，{an}是递减的且an＜1，最小值正在其中，也就是a9.

当n=10，11，12，…时，{an}是递减的且an＞1，最大值正在其中，也就是a10.

如图所示，数列的图象是一些离散的点，它的两部分被直线y=1和分开了，其中左侧只有9个点.

例8图

说明：本题的分离变量的方法和分类讨论是研究成功的关键.通过对自变量取值范围的合理分类，我们更加深刻理解了函数单调性与数列性质的相互关系.如果你在分离变量之后，作出该数列的大致图象（它被直线y=1分割成上下两个部分，都是些离散的点），数形结合一下，我们的理解会更上一层楼.

这道题也可以采用导数的方法，结合离散的函数图象，注意定义域，问题可能也很容易解决.请试试看！

例9 已知函数

（1）试判断f（x）在定义域内的单调性；

（2）若f（x）在[1，e]上的最小值为，求实数a的值；

（3）若f（x）＜x2在（1，+∞）上恒成立，求实数a的取值范围.

探究：（1）f（x）的定义域是（0，+∞），且

由可得f（x）在x＞-a时为增函数，但-a不知在何处，所以把x＞-a与定义域取公共部分，在数轴上把x＞-a与x＞0画出来.随着-a的运动变化，分类讨论的标准就逐步确立下来了.

①若-a≤0即a≥0，则上述交集为整个定义域，即f'（x）≥0恒成立，故f（x）在（0，+∞）上单调递增.

②若-a＞0即a＜0，则上述公共部分为x＞-a，此时f'（x）＞0，故f（x）在（-a，+∞）上单调递增，在（0，-a）上单调递减.

（2）由（1）的经验，我们也要在定义域[1，e]上讨论函数的单调性，x＞-a与定义域[1，e]取公共部分，在数轴上把x＞-a与[1，e]两个区间画出来.随着-a的运动变化，分类讨论的标准就逐步确立下来了.

①若-a≤1即a≥-1，则x+a≥0恒成立，即f'（x）≥0在[1，e]上恒成立，此时f（x）在[1，e]上递增，

所以，所以（舍）.

②若-a≥e即a≤-e，则x+a≤0恒成立，即f'（x）≤0在[1，e]上恒成立，此时f（x）在[1，e]上递减，

所以，所以（舍）.

③若1＜-a＜e即-e＜a＜-1，上述公共部分为-a＜x＜e，

当-a＜x＜e时，f'（x）＞0，所以f（x）在（-a，e）上递增；

当1＜x＜-a时，f'（x）＜0，所以f（x）在（1，-a）上递减.

所以，所以

综上，

（3）因为

所以a＞xlnx-x3恒成立.

令g（x）=xlnx-x3，

因为当x∈（1，+∞）时，h'（x）＜0，

所以h（x）在（1，+∞）上递减，

所以h（x）＜h（1）=-2＜0，即g'（x）＜0，

所以g（x）在（1，+∞）上递减，

所以g（x）＜g（1）=-1，

所以a≥-1时，f（x）＜x2在（1，+∞）上恒成立，

即a的取值范围为[-1，+∞）.

说明：一般方法与本题的具体定义域相结合，在取交集的过程中逐步确定分类讨论的标准.在这个过程中，我们对函数的变量方法有了更加清醒的认识：不变是相对的.变是绝对的.参变量的控制与影响力是本题的主要特点.