高中数学思想方法：数形结合在各数学领域广泛应用

（一）解决方程、不等式、函数和导数问题

方程、不等式、函数和导数这四类重要数学问题，具备高度的相关性和融合性，它们之间往往可以相互转化、相互借鉴、相互印证、相互启迪.依据函数性质修正完善函数图象，然后借助于图象进一步研究函数的深层性质，是常用的数形结合方式.图象的几何特征与函数的相关性质紧密结合，可以使问题更加直观更加明确，进而使问题研究更加深刻更加直接更加精准.

处理方程问题时，可以把方程的根的问题看作一个函数的零点或者两个函数图象的交点问题；处理不等式时，可以从题目的条件与结论出发，联系相关函数，着重分析其几何意义，这样，从图形上一般都能比较直接的找出解题的思路.

例19 f（x）=|x+1|+|x-3|的最小值是________，单调增区间为________，其图象的对称轴方程为_________.

探究：该函数的几何意义为数轴上动点x到两个定点-1和3的距离之和.

画出数轴，让x左右运动，可以发现当x在-1和3之间的时候，距离和的最小值为4，

当x在-1的左侧时，随着x的增大，距离和变小；当x在3的右侧时，随着x的增大，距离和变大，所以函数的单调增区间为（3，+∞），-1和3的中点为1.依据图象的对称性可知，当x在1的两侧与1等距离时，上述距离和相等，所以函数图象的对称轴为x=1.

例20 已知函数f（x）对定义域R内的任意x都有f（x）=f（4-x），且当x≠2时，其导函数f'（x）满足xf'（x）＞2f'（x），若2＜a＜4，则（ ）.

A.

B.

C.

D.

探究：这是一道选择题，条件和结论都很复杂.从结论的选项中可以看出，大概是利用函数的单调性判断函数值的大小.

例20图①

例20图②

显然，4＜2a＜16，画出函数y=x和y=lnx的图象（y=lnx的一条切线为y=x-1）可知，2＜a＜4的时候a＞lna＞0，

所以，所以

再去发展条件：由f（x）=f（4-x）可得：函数y=f（x）图象的对称轴为x=2.

由xf'（x）＞2f'（x）可得：（x-2）f'（x）＞0，

所以x＞2时，f'（x）＞0，f（x）为增函数；x＜2时，f'（x）＜0，f（x）为减函数.

根据上述信息画出y=f（x）的图象，如例20图②所示：自变量离开对称轴越远函数值越大，显然答案为B.

说明：本题里多次运用数形结合，多次把题目的条件转变成函数的图象特性，使得问题越来越清晰.

例21 已知关于x的不等式（ax2+a2x-2）lnx≥0在x＞0时恒成立，则实数a的取值集合为________.

探究：首先利用代数方法将问题转化为：

当lnx≥0时，ax2+a2x-2≥0；也就是x≥1时，ax2+a2x-2≥0.

当lnx≤0时，ax2+a2x-2≤0；也就是0＜x≤1时，ax2+a2x-2≤0.

要使上述两个要求同时成立应该考虑对应二次函数的图象，进入几何方法范畴.

设f（x）=ax2+a2x-2，根据上面两个要求，二次函数图象必须开口向上而且“穿过”点（1，0），也就是a＞0且f（1）=0，

如图所示，易得到a=1.

例21图

例22 （1）已知关于x的方程x2-4|x|+5=m有四个不相等的实根，则实数m的取值范围为_________.

（2）求定积分

（3）若loga2＜logb2＜0，则（ ）.

A.0＜a＜b＜1 B.0＜b＜a＜1

C.a＞b＞1 D.b＞a＞1

（4）关于x的方程a|x|=x+a有两个不同的根，则实数a的取值范围是（ ）.

A.(1,+∞) B.(-1,1)

C.(-∞,-1]∪[1,+∞) D.(-∞,-1)∪(1,+∞)

（5）对a，b∈R，记则则函数f（x）=max{|x+1|，|x-2|}（x∈R）的最小值是________.

探究：（1）直接求解，太烦琐！由方程联想二次函数进行数形结合.

设f（x）=x2-4|x|+5.显然这是一个偶函数，画出它与y=m的图象可知1＜m＜5.

（2）按照传统方法，“求原函数”很难，所以应该转向研究定积分的几何意义.

例22（1）图

函数（可以化为x2+y2=1（y≥0）），与x轴围成区域的面积（半圆）就是定积分的几何意义：

例22（3）图

（3）显然，0＜a＜1，0＜b＜1，画出函数y=logax与y=logbx的图象，容易看出二者与直线y=1的交点横坐标分别是a，b，如例22（3）图所示.

答案：B.0＜b＜a＜1.

（4）画出y=a|x|与y=x+a的图象函数，它们恰有两个公共点.前者是一对射线，“开口”方向由a的符号决定；后者是一条直线，斜率一定，在y轴上的截距也由a决定，所以a的符号是问题分类和作图的标准.

如例22（4）图：

情形1：

情形2：

例22（4）图

注意：当直线的倾斜角为锐角时，倾斜角越大，其斜率越大；同样，当直线的倾斜角为钝角时，倾斜角越大，其斜率也越大.

（5）可以尝试去画出f（x）=max{|x+1|，|x-2|}（x∈R）的图象，也就是画出y=|x+1|与y=|x-2|两个图象，它们有一个交点，然后对每一个x，我们留下二者中的较大者.由最后的完整的f（x）的图象不难发现，其最低点为

说明：在研究函数方程不等式有关的选择填空题的时候，数形结合往往特别奏效；难度越大，我们越应该在这方面有所倾斜.

例23 f（x）=-x2+8x，g（x）=6lnx+m，若两个函数图象有三个交点，求m的取值范围.

探究：依题意，欲使f（x），g（x）有三交点，f（x）=g（x）必有三实根.

-x2+8x=6lnx+m，即x2-8x+6lnx+m=0.

例23图①

不妨设h（x）=x2-8x+6lnx+m，

考察该函数的基本性质：

得：0＜x＜1或x＞3.

例23图②

于是，得到h（x）：0＜x＜1时函数单调递增，1＜x＜3函数单调递减，x＞3时函数单调递增，x=1时取得极大值，x=3时取得极小值.

可以画出y=h（x）的粗略图象，由图可得要使h（x）=0有三实根，只需h（1）＞0，h（3）＜0.

代入容易解得7＜m＜15-6ln3.

说明：两个函数图象的交点问题转化成了一个方程的求解.不会解的方程，一般来说都转化成函数的零点问题.所有的转化，数形结合都在起到引导的作用.

例24 若f（x）是三次函数，且f'（x）=-x2+4mx-3m2（0＜m＜1），f（0）=1.

（1）求f（x）的极值；

（2）若x∈[0，m+2]，求f（x）的最大值和最小值.

探究：显然，

（1）由f'（x）=-x2+4mx-3m2＞0可得f（x）的单调增区间为（m，3m），

所以f（x）的单调减区间为（-∞，m）和（3m，+∞）， 所以函数的极大值、极小值分别为f（3m）=1，

例24图

（2）x∈[0，m+2]，0＜m＜1，所以m+2＞3m，也就是极小值点极大值点都在定义域内.画出函数的大致图象可以发现，x∈[0，m+2]时，函数的最大值为f（0）=f（3m）=1，最小值为f（m）与f（m+2）中的更小者

将二者作差比较可得

当时，函数最小值为

当时，函数最小值为

说明：画出函数图象，可以避免很多不必要的讨论.

（二）数形结合在解析几何中的应用

解析几何的基本思想就是数形结合，几乎每一个解析几何问题都兼有代数和几何两个方面的信息，解决方法往往都是数形结合的产物.

例25 已知P为圆M：（x-3）2+（y-4）2=1上一动点，A（-1，0），B（1，0），求|PA|2+|PB|2的最大值和最小值.

探究：设P（x，y），则|PA|2+|PB|2=2（x2+y2）+2，有点为难！

如果我们关注图形，应该不难联想到问题可以转化为|PA|2+|PB|2=2|PO|2+2.

当点P在OM的连线上的时候|PA|2+|PB|2=2|PO|2+2的最大值、最小值分别为74，34.

例25图

说明：当我们在解题过程中难以为继的时候，可以考虑在数形结合方面有所转换.另外，如果在研究过程当中，我们的视野能够在题给条件和几何图形上不断比对，自觉地发现新思路也是个大概率事件.

例26 已知P是直线3x+4y+8=0上的动点，PA，PB是x2+y2-2x-2y+1=0的两条切线，A，B是切点，C是圆心，求四边形PACB面积的最小值.

探究：如图：

例26图

因为=|PA|，

P，A两点都是动点，不便于研究和把握，应该考虑在直角三角形PAC中，将问题转化为与定点C有关的便于把控的问题.

因为

要使面积最小，只须PC最短，即定点C到定直线上动点P距离最小即可，即点C（1，1）到直线3x+4y+8=0的距离，

而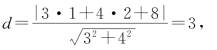

所以

说明：数形结合本身就是一种转化.在这个过程中不断地化繁为简、化间接为直接、化动为静，有利于问题的解决.

本题中，四边形的面积化成了三角形的面积，两端点都变动的线段变成了一端固定的.

例27 曲线x2+y2-2|x|-2|y|=0围成图形的面积为（ ）.

A.8+4π B.4+4π

C.8+2π D.4+8π

探究：可以分四种情况（四个象限），分类讨论去掉绝对值符号，画出方程的曲线.

很容易看出曲线分别关于坐标轴、坐标原点都对称，所以只要画出第一象限的图象即可.

第一象限内，即x≥0，y≥0时，方程可化为x2+y2-2x-2y=0.

这是一段圆弧，圆心M（1，1），与坐标轴的交点分别为O（0，0），A（2，0），B（0，2）.如图所示

例27图

可以发现，M为AB的中点，所以AB为圆的直径，所以方程的曲线为四个半圆以及它们的直径构成的正方形.所求面积为8+4π.

说明：精确作图，对发现问题的简洁解法，避免误入歧途，都十分重要.

解题过程中，力求精准作图，尤其是那些关键点关键线.比如，抛物线的顶点对称轴、圆的圆心、函数的极值点、图象与坐标轴的交点甚至图象的发展趋势，都要力求精准，它们对获得问题的解决方法至关重要.

例28 已知实数x，y满足x2+y2-6x+7=0，求：

（1）的最值；（2）y-x的最值；（3）x2+y2的最值.

探究：这是条件最值问题，消元法难有进展，不好构建函数，但我们可以关注条件和结论的几何意义，对问题进行转化.

方程x2+y2-6x+7=0等价于（x-3）2+y2=2，表示圆心在（3，0），半径为的圆.

的几何意义是圆上一点与原点连线的斜率.

令y-x=b，则b是y=x+b在y轴上的截距.

x2+y2是圆上一点与原点的距离的平方.

例28（1）图

（1）设，即y=kx.由例28（1）图可知，当直线y=kx与圆相切时，斜率k取得最大值和最小值.此时

此时(www.xing528.com)

所以

（2）设y-x=b，即y=x+b.

由例28（2）图可知，当y=x+b与圆相切时，纵截距b取得最大值和最小值.

例28（2）图

由，解得b=-1，b=-5，所以（y-x）max=-1，（yx）min=-5.

（3）x2+y2表示圆上的点与原点距离的平方，由例28（3）图易知答案为：最小值为，最大值为

例28（3）图

说明：解析几何的问题中，只要是与直线和圆的方程有关的，一般都可以转化成几何问题，从而获得比较简洁的解法.因为这样一来，初中的知识、方法能够得到直接应用，而且可以避开那些复杂的运算.

例29 正方形ABCD在直角坐标平面内，已知其一条边AB在直线y=x+4上，C，D在抛物线x=y2上，求正方形ABCD的面积.

探究：画出图形，如图所示，设CD所在的直线方程：y=x+b.

由两条平行线距离公式可得正方形的边长=

例29图

把直线y=x+b代入抛物线方程可得：

x2+(2b-1)x+b2=0.

设C（x1，y1），D（x2，y2），则x1+x2=1-2b，x1x2=b2.

由弦长公式可得正方形边长，

所以

容易解得b=-2或者b=-6，

进而正方形面积S=18或者50.

例30 给定椭圆方程，求与这个椭圆有公共焦点的双曲线，使得以它们的交点为顶点的四边形面积最大，并求相应的四边形的顶点坐标.

探究：如图：

显然，四边形为矩形，它是椭圆的内接矩形，我们先研究它的最大面积，然后依据交点和焦点的情况进一步确定双曲线的方程.

例30图

A在第一象限，利用椭圆的参数方程可设，则矩形面积

显然，当α=45°时，矩形面积最大，此时

双曲线的焦点与椭圆相同：

容易得到以F为焦点且过A点的双曲线方程为y2-x2=1.

说明：几乎所有的解析几何问题，画出图形后都会给我们直接的启发，要么启迪思路，要么简化运算.

在计算椭圆内接矩形最大面积的时候，也可以使用均值不等式.

设A（x，y），则，所以

而矩形的面积（当且仅当时取等号）.

在高中数学里，考查运算能力的最高点就是解析几何，明确运算目标、选择运算途径、简化运算过程都是对数学能力的较高要求，具备数形结合意识，往往能够有意外收获.这其实都在情理之中.

如果你对自己的运算能力有足够的自信，也可以通过研究椭圆与双曲线的交点坐标来建立内接矩形面积的目标函数.

椭圆与双曲线的半焦距均为，焦点都在y轴上，所以可设双曲线方程为：

，即

与即y2+2x2=4联立可得（加减消元法），这是一个令人振奋的结果，

所以x=b，进而，矩形的面积

接下来，可以用均值不等式和二次函数的方法得到：

矩形面积最大时，b=1.

（三）几何数列问题

数列的通项公式和前n项和公式都是特殊的函数，对它们的研究，如果结合函数图象，肯定会事半功倍的.这方面的问题我们已经比较熟悉了、现在看数列问题延伸——几何数列.

将数列中的项，按照一定的结构排列成一个几何图案.在这个图案中，给出一定的条件，要求结合数列性质和图案特征.研究相应的问题，为了表述方便，我们称其为几何数列问题.

几何数列的研究，当然离不开数形结合，需要我们在几何图形上，不断开发数列的各种性质；如果二者结合得好，问题一般都会迎刃而解.

例31 n2个正数排成n行n列：

a11 a12 a13 a14…………其中每一行的数成等差数列，

a21 a22 a23 a24…………每一列的数成等比数列，

a31 a32 a33 a34…………并且所有公比相等.

a41 a42 a43 a44………已知：，amn表示第m行第n列处的元素，

……

（1）求amn的表达式；（2）求这n2个数的和.

探究：这个问题，初看起来比较复杂，但是如果我们结合图象将题目条件标注在图案上，问题便明朗起来了

（1）请看信息最丰富的第四行，显然该等差数列的公差为，进而首项，第四项为

此时第四列的信息也丰富起来了，这是一个等比数列，显然公比为首项为2，每一列的公比都为

我们再去关注一下第一列，这也是一个等比数列，公比也为，它的第四项，所以首项

所以第一行中首项，第四项为2，这是一个等差数列，公差d=，通项公式

再看第n列，这是一个等比数列，公比为，首项，其（第m项）通项公式

（2）第一行的和为，以后每一行的和以的比例递缩，所以这些数的和为

说明：将题设条件搬运到数列图案之中，形象直观，各种关系一目了然，甚至一些计算和推理都可以在图案上进行，大大降低了探索研究的难度.

例32 （1）设{an}是集合{2s+2t|0≤s＜t且s，t∈Z}中所有的数从小到大排列成的数列，即a1=3，a2=5，a3=6，a4=9，a5=10，a6=12，….

将数列{an}各项按照上小下大，左小右大的原则写成如下的三角形数表：

①写出这个三角形数表的第四行、第五行各数；②求a100；

（2）设{bn}是集合{2r+2s+2t|0≤r＜s＜t}，且r，s，t∈Z}中所有的数从小到大排列成的数列，已知bk=1160，求k的值.

探究：请注意这样一个事实：对任意正整数n都有2n+2＞2n+1+2n，甚至2n＞2n-1+2n-2+2n-3+…+1.

（1）①用（t，s）表示2t+2s，根据列举法利用前几个数找到其规律，是每一个的横坐标从0增加到对应的行数，而纵坐标为行数，就可求出第四行、第五行各数.

表格的规律为：

3=(0，1).

5=(0，2)，6=(1，2).

9=(0，3)，10=(1，3)，12=(2，3).

第四行：17=（0，4），18=（1，4），20=（2，4），24=（3，4）.

第五行：33=（0，5），34=（1，5），36=（2，5），

40=(3，5)，48=(4，5).

②因为100=（1+2+3+4+…+13）+9，所以可以知道a100位于第14行第8列，即可求出a100=（8，14）=28+214=16640.

（2）方法1：210＜1160＜211，1160-210=136，27＜136＜28，136-27=8=23，

所以bk=1160=210+27+23.

令M={c∈B|c＜1160}（其中，B={2r+2s+2t|0≤r＜s＜t}）.

因M={c∈B|c＜210}∪{c∈B|210＜c＜210+27}∪{c∈B|210+27＜c＜210+27+23}.

现在求M的元素个数：

{c∈B|c＜210}={2r+2s+2t|0≤r＜s＜t＜10}，r，s，t是从0，1，2…9任意选取的三个不同数字的组合，所以其元素个数为C310.

{c∈B|210＜c＜210+27}={210+2s+2r|0≤r＜s＜7}.s，t是从0，1，2…6任意选取的两个不同数字的组合，所以某元素个数为C27.

{c∈B|210+27＜c＜210+27+23}={210+27+2r|0≤r＜3}.r是从0，1，2任意选取的一个数字，所以某元素个数为C13：k=C310+C27+C13+1=145.

方法2：规定2r+2s+2t=（r，s，t），bk=1160=23+27+210=（3，7，10），

则b1=20+21+22=（0，1，2），最高次数为2，则另外两个数字的选择只有C22种

最高次数为3，则另外两个数字的选择只有C23种：

(0，1，3)(0，2，3)(1，2，3).

最高次数为4，则另外两个数字的选择只有C24种：

(0，1，4)(0，2，4)(1，2，4)(0，3，4)(1，3，4)(2，3，4)…

最高次数为9，则另外两个数字的选择只有C29种….

最高次数为10，则另外两个数字的选择只能从0，1，2，…，6中选两个，有C27种，再加上（0，7，10）（1，7，10）（2，7，10）（3，7，10），共有四个，

所以k=（C22+C23+…+C29）+C27+4=145.

说明：请看充分关注并利用数列方阵中的代数和几何信息，对获得问题的思路和简化运算会有巨大的作用.几何图形的直观显示出强大的力量，它给了我们异常清新的结构提示.

把问题转化成坐标表示，除了把问题结构变得简约明快之外，也使得我们有了结构方面的依靠.

例33 将数列{an}中的所有项按每一行比上一行多一项的规则排成如下数表：

a1

a2a3

a4a5a6

a7a8a9a10

记表中的第一列数a1，a2，a4，a7，…构成的数列为{bn}，b1=a1=1.

Sn为数列{bn}的前n项和，且满足

（Ⅰ）证明数列成等差数列，并求数列{bn}的通项公式；

（Ⅱ）上表中，若从第三行起，每一行中的数按从左到右的顺序均构成等比数列且公比为同一个正数.当时，求上表中第k（k≥3）行所有项的和.

探究：（Ⅰ）注意到结论是：数列成等差数列，所以应该将bn的信息转化成的结构.

由已知，当n≥2时，所以

即，所以

又S1=b1=a1=1，

所以数列是首项为1，公差为的等差数列.

由上可知

即

所以当n≥2时，

因此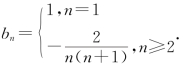

（2）设上表中从第三行起，每行的公比都为q，且q＞0.

因为，所以表中第1行至第12行共含有数列{an}的前78项，

故a81在表中第13行第三列，因此

又，所以q=2.

记表中第k（k≥3）行所有项的和为S，

则

说明：在数列图案中，位置信息甚至比代数信息更重要，因为明确了位置信息，便可以非常便捷地找到代数关系，所以这类问题的解决中数形结合特别重要.很多研究可以直接在图案中进行，运用得当，不仅事半功倍，而且在解题过程中肯定会左右逢源！

总之，数形结合包含“以形助数”和“以数辅形”两个方面，它们在数学研究中，应该不是单一的一种方式，两种方式综合起来会事半功倍.数学研究过程中，建立数形结合的自觉意识，解题过程中我们的运算和思维肯定会长出一双隐形的翅膀，带你飞，给你希望，让你所有的思想都开花.它能使你在“漫长黑暗”的探究中，不经意间带给你灵感和希望！