高中数学思想方法：三个数形结合原则解决问题

（一）等价性原则

数形结合的过程中，代数性质和几何性质的转换研究必须是等价的；否则，研究的就不是原来的问题了，解题过程要么会出现遗漏以偏概全，要么无意当中忽视问题的约束条件，放大了问题的研究范围，使得问题研究无的放矢.

要充分注意图形的局限性，它有时候不能完整地表现数的严谨性、全面性、一般性.这时，图形的性质只能是一种直观而浅显的说明，要注意其带来的负面效应.

例8 （1）圆与坐标轴都相切且过点M（1，2），这个圆的方程为_________.

（2）命题p：“当a＞1时，关于x的方程ax=logax无实数解”.命题q：“函数y=x2与y=2x的图象共有两个交点”，判断命题p∨q的真假.

例8图①

探究：（1）容易发现：点M的纵坐标是横坐标的两倍.

如例8图①，圆心N刚好在点M的正下方，N（1，1），所以圆的方程为（x-1）2+（y-1）2=1.

其实，这是一个片面的结论：根据题意应该假设圆的半径为r，则圆心坐标N（r，r），则圆的方程可设为（x-r）2+（y-r）2=r2.

将M（1，2）代入可得r=1或r=5，

所以圆的方程为：（x-1）2+（y-1）2=1.或（x-5）2+（y-5）2=25，如例8图②所示.

（2）在同一坐标系中，分别画出函数y=ax（a＞1）及y=logax（a＞1）的图象，如例8图③所示，可见它们没有公共点，所以方程确无实数解，故命题p正确.

例8图②

这是一个错误的结论，因为对不同的实数a，y=ax及y=logax的图象的延伸趋势不同.例如当a=2时，原方程无实数解；而当时，x=2便是原方程的解.这说明两图象向上延伸时，一定相交且交点就在直线y=x上.

上面的错判就是潦草作图，而画出了个以偏概全的图形，你能画出与的图象吗？如例8图④，（2，2），（4，4）就是它们的交点.

在指数函数与其反函数y的图象上，不仅在直线y=x上有一个交点，而且和这两点也应在它们图象上，所以它们应该至少有三个交点.问题比我们的直观想象复杂得多！

例8图③

例8图④

函数y=x2与y=2x的图象其实有三个交点，但是如果草率作图会误以为只有两个交点.如例8图⑤所示.如果结合函数的变化率，后者指数函数在x＞0时增长得更快，y轴右侧第一个交点后，还会再相交一次，y轴左侧一个交点，y轴右侧两个交点：（2，4），（4，16）.这样一来，命题p∨q为假.

例9 椭圆方程为

例8图⑤

（1）点P在椭圆上，P到椭圆短轴的上顶点A的距离为2，这样的点P共有多少个？说明原因.

（2）过椭圆短轴的上顶点A作两条互相垂直的直线另交椭圆于B，C，若|AB|=|AC|，这样的直线有多少组？求其方程.

探究：如果画出图形，很容易发现：椭圆的上顶点坐标为A（0，1），当点P成为椭圆的下顶点P（0，-1）的时候，P到椭圆短轴上顶点的距离为2；当过点A的两条直线关于y轴对称且互相垂直的时候，|AB|=|AC|.此时它们的方程为y=x+1，y=-x+1.

这是问题的唯一答案吗？好像有点太过简单了，我们应该利用代数方法严谨推算，才能将答案“一网打尽”.

例9图

（1）设点P（x，y），|PA|=2，所以x2+（y-1）2=4.

又，所以联立可得3y2+2y-1=0，所以y=-1或

代回原方程可得所求的点一共有三个：

（2）假设直线AB和AC的方程分别为：y=kx+1和0）.

将y=kx+1代入椭圆方程可得（1+4k2）x2+8kx=0，

所以x=0或所以

同理可得

所以

所以k3-4k2+4k-1=0.

依据前面的图象可知这个方程肯定有一根为1，

所以上式可以因式分解为（k-1）（k2-3k+1）=0，所以

这样一来，所求的两条直线共有三组.

说明：上面几个问题的举证，完全得益于我们全面严谨的思考.代数推理和计算的严谨性，使它的方法总能把结论“一网打尽”，而几何方法很有可能以偏概全.

但是，如果仅仅考虑问题的代数特征，由于代数特征的隐蔽性和复杂抽象性，我们可能看不到它的全部信息而贸然下结论，也可能以偏概全导致失误.

例10 “x＞1且y＞1”是“x+y＞2且xy＞1”的（ ）.

A.充要条件 B.充分不必要条件

C.必要不充分条件 D.既不充分又不必要条件

探究：看到该题，可能考虑不到问题的全貌，往往可能误以为“x＞1且y＞1”与“x+y＞2且xy＞1”是等价的.

对后者的解仅限于表面的粗浅的理解，当然有些同学会根据几个特例反例来验证二者的非等价关系.其实，如果画出图形，如图所示，由图可以看出“x＞1且y＞1”是“x+y＞2且xy＞1”的子集，答案明显为B.

例10图

说明：几何图形有形象、直观的优点，适合于对问题进行定性分析，但在定量研究方面还必须借助代数的计算；特别是对于较复杂的“形”，不但要正确地把图形数字化，而且还要留心观察图形的特点，发掘题目中的隐含条件，充分利用图形的性质或几何意义，把“形”正确表示成“数”的形式，进行精确的分析和计算.

图形虽然直观、形象，但它只是一个部分而不是全部，甚至有些图形是有误差的，并不准确，所以我们不能以偏概全，不能简单地根据图形获取答案；就是要用到图形，我们在作图时也要注意细节的精准，要注意函数图象的延伸趋势，甚至结合代数推理进行确认.

几何作图不能代替代数证明，证明某些代数结论，其实也就是证明其相应的几何特征；如果用直观图形来证明，其实是一个逻辑循环，用结论来证明结论显然不可信.

（二）互补性原则

在数形转换的过程中，不要刻板地、单纯地使用代数法或者几何法，组合拳更有威力.既要进行几何的直观分析，又要进行相应的代数的抽象探求；既要关注问题的代数特征，又要联想问题的几何含义.仅仅研究问题的几何背景或者代数意义，往往举步维艰；代数几何双方互相印证、互相补充，才能使解题更精准更高效.

例11 小明、小林和小颖共解出100道数学题，每人都解出了其中的60道，如果将其中只有1人解出的题叫作难题，2人解出的题叫作中档题，3人都解出的题叫作容易题，那么难题比容易题多几道？

探究：如图：

假设容易题数为x，中档题数为y，难题数为z.

由题意结合图形可得x+y+z=100.……①

但是，三个人总共解出了180道题，其中容易题是正中间部分，被数了三次，中档题在图中被覆盖过两次，最边缘的部分为难题，所以3x+2y+z=180.……②

此时，我们应该把目光从图形上转移到上述两个方程上来，兼顾到结论，消去y是正常选择：①×2-②可得z-x=20，也就是难题比容易题多20道.

说明：结合图形能比较容易地发现两个方程，兼顾到结论的要求，在代数结构中，把y消掉，很可能就得到结论了.这是一种很自然的措施.几何方法和代数方法的优雅转换，真让我们开心！

例11图

例12 自行车选手甲、乙、丙三人同时从A点出发沿着AB，BC，CA三条直线段行进，选手甲在这三条直线上行进的速度分别为12，10，15（km/h），选手乙在这三条直线上行进的速度分别为15，15，10（km/h），选手丙在这三条直线上行进的速度分别为10，20，12（km/h）.若三名选手同时到达终点A，求sinA+sinB+sinC的值.

例12图

探究：问题有九个数据，真有些难以招架.在这种情况下，审题的第一步就是画图，把题目中的所有信息“搬运”到图形上，面对图形以及“搬运”来的代数数据，条件和结论的所有信息“尽收眼底”一目了然，数形结合便势在必行了，如图所示.

问题中有两类未知量，“每段路程（三角形的三条边长）和三个人在每一段上所用的时间”，如果研究时间，由九个未知数（太多），兼顾到结论，我们更应该关注三条边长（三段路程三个未知数）.由于三人总用时相等，这本身就是一个方程组，所以：

这是一个方程组，去掉分母是一种化简……合并同类项也是一种化简……消元更是一种化简……

把b看成已知数可得

显然，三条边长符合勾股定理，

说明：不断地在图形和问题条件结论之间进行转换，图形分析和方程组的研究方式相互印证、相互补充，就能得到不同的启发，从而使得问题的解决更有方向、更有确定性.

例13 求函数y=x2+|x-a|+1的值域.

探究：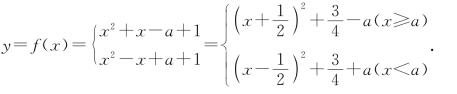

这是一个连续函数，它在x=a处也是连续的.去绝对值化为分段函数，再按直线x=a相对于两抛物线的对称轴的位置分类讨论，我们的视野和思路在图象和函数表达式之间不断地跳转.几何图象指引我们正确的方向，代数计算与之形成互补，二者可以相辅相成、相得益彰.

（1）当时，如例13图①知

（2）当时，如例13图②所示知y≥f（a）=a2+1.

（3）当时，如例13图③所示知，

综上所述，当时，值域为

当时，值域为[a2+1，+∞）；

当时，值域为(www.xing528.com)

例13图

说明：数形结合与分类讨论两大数学思想的完美结合，通过对函数图象的动态观察，结合代数表达式的分析，二者形成互补，我们对问题的整体性就有了明确认识.

例14 函数

（1）求f（x）的单调区间；

（2）f（x）在x∈[1，2]的最大值；

（3）若函数的定义域为{x|x≤-1或x≥1}且f（x）最小值为，求k的值.

探究：（1）由可得x≥k.所以函数的单调增区间为[k，+∞），而（-∞，0）和（0，k）为减区间.

（2）根据函数的单调性，可以发现f（x）在x∈[1，2]的图象为下凸函数，如图所示，

所以其最大值为f（1）与f（2）中的更大者，

最大值：

（3）结合函数的图象，当x≤-1或x≥1的时候，函数的最小值与极小值点x=k在定义域中的相对位置密切相关；

当k≥1时，函数最小值为f（-1）=1-2k3与f（k）=3k2的更小者，显然它不可能等于

例14图

当0＜k＜1时，函数最小值为f（-1）=1-2k3与f（1）=1+2k3的更小者1-2k3，所以，则

总之，

说明：请看本题的数形结合多么和谐自然.利用代数方法遇到困难的时候，我们的视野很自然地就转到几何图形上来了，在几何图形上明确思路以后，我们又可以回到代数方法上去，进行更细致、更准确的推算.

（三）有利性原则

不要为了“数形结合”而数形结合.具体解题时，一要考虑是否可行和是否有利；二要选择好突破口，适时转化；三要挖掘隐含条件，尤其要注意几何背景下的数量关系和代数语言里包含的几何图形.当我们使用代数法进展顺利的时候，可以暂时放弃几何方法；当我们在几何计算或证明方面得心应手的时候，也应该乘胜前进.只有当代数方法（几何方法）一筹莫展的时候，我们才应该考虑方法或者知识的转换.

例15 ，a，b∈R且a≠b，求证：|f（a）-f（b）|＜|a-b|.

探究1：直接联想到几何模型而进行数形结合.

因为a≠b，不妨设a＞b，构造如图所示的Rt△OAP，其中OP=1，OA=a，OB=b，

例15图

则AB=a-b.

在Rt△OAP中，有|PA-PB|＜AB，

所以|f（a）-f（b）|＜|a-b|.

探究2：采用分析法，

要证|f（a）-f（b）|＜|a-b|，

也就是要证

面对上面的“呆板”的结构特征，我们最好的选择就是求变：

上式等价于（分子有理化），

也就是

该不等式显然成立，所以原不等式正确.

说明：上面两种方法，第一种极富想象力和创造性，把一个代数问题转化成了一个简单的几何问题，过程简洁明快，但这并不是人人都能做到的；第二种方法采用不等式证明的常规思路——分析法，通过分子有理化对问题进行变形，问题也得到顺利解决.

你认为上述两种方法都完美无缺吗？找到它们的遗漏并进行补充修正，这就是研究型阅读，批判性学习可以使你更快地成长.

我们是否应该对a，b的符号分类讨论一下呢？

研究数学问题的时候，不要提前设定某一种固定的方法，应该实事求是、具体问题具体分析，在问题的发展化简的过程中逐步确定其研究方法，否则会走入形而上学的死胡同.

例16 在平面直角坐标系中，A（0，0），B（3，0），C（4，3），D（0，4），P为动点，则点P到上述四点距离和的最小值为_________.

探究：如果从代数角度考虑，假设点P（x，y），构建距离和的目标函数……四个根号两个自由变量，难以为继，所以考虑转换成几何问题是一个有利的选择.

显然，点P在四边形的内部，连接PA，PC，显然当它们“拉直”（共线）的时候，PA+PC最短，如图所示.

例16图

同理，连接PB，PD，当它们共线的时候，PB+PD最短.

综上所述，当P为四边形对角线交点的时候，PA+PC+PB+PD的最小值为两条对角线长度之和，该值为10.

说明：其实，读完这道题，我们就能“听见”数形结合的“声音”了，使用几何方法一气呵成，问题得到圆满解决.

例17 求函数f（x）=（x2-3x+1）ex的最小值.

探究：f'（x）=（x2-x-2）ex≤0可得函数的单调减区间为[-1，2]，函数的单调增区间为（-∞，-1）和（2，+∞），所以函数的极大值为f（-1）=，极小值为f（2）=-e2.

根据以上信息可以画出函数的大概图象，但是这个图象可能是不确切的.我们可以根据代数表达式，进一步分析函数的性质，从而进一步丰富完善函数的图象.

例17图

由表达式可以看出函数只有两个零点.

在极大值点的左侧，也就是x＜-1的时候，f（x）＞0恒成立，结合图象不难得到函数的极小值就是最小值，如图所示.

说明：很显然，该问题的处理过程中，结合函数表达式反映出来的代数性质的分析，不断地对函数图象进行修正和完善，充分体现了有利性原则.

例18 已知函数f（x）=x3+3|x-a|（a∈R）.

（1）求函数的单调区间；

（2）若f（x）在[-1，1]上的最大值和最小值分别记为M（a），m（a），求M（a）-m（a）.

探究：（1）因为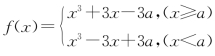，所以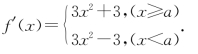

在同一坐标系中分别画出函数y=3x2+3与y=3x2-3函数的图象，如图所示，可以发现：

例18图

当a≤-1时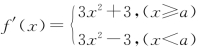，恒为正数，f（x）在R上是增函数.

当-1＜a＜1时，f'（x）在（a，+∞）上为正，在（-1，a）上为负，在（-∞，-1）上为正，

所以f（x）的增区间为（a，+∞）和（-∞，-1），减区间为（-1，a）.

当a≥1时，f'（x）在（1，+∞）上为正，在（-1，1）上为负，在（-∞，-1）上为正，

所以f（x）的增区间为（1，+∞）和（-∞，-1），减区间为（-1，1）.

（2）当a≤-1时，f（x）在[-1，1]上是增函数，f（x）=x3+3x-3a，因此M（a）=f（1）=4-3a，m（a）=f（-1）=-4-3a，M（a）-m（a）=4-3a-（-4-3a）=8.

当-1＜a＜1时：

f（x）在[-1，a]上单调递减，f（x）=x3-3x+3a；

f（x）在[a，1]上单调递增，f（x）=x3+3x-3a，

所以m（a）=f（a）=a3，

M（a）为f（1）与f（-1）的较大者.

由于f（1）-f（-1）=-6a+2，

因此，当时，M（a）-m（a）=-a3-3a+4.

当时，M（a）-m（a）=-a3+3a+2.

当a≥1时，f（x）在[-1，1]上为减函数，f（x）=x3-3x+3a，

因此M（a）=f（-1）=2+3a，m（a）=f（1）=-2+3a，

故M（a）-m（a）=2+3a-（-2+3a）=4.

说明：这是一个难题.可以看出，导函数的图象对指导原函数单调性和最值研究意义重大.第（2）题几乎完全利用第（1）题的图象和单调性结论，可以避开三次函数的图象直接进入问题的本质，这又一次体现了有利性的原则.