高中数学问题研究中数形结合思想的作用

数形结合可以明确解题思路，发现或者构造问题的简单解法.

数形转换的过程中，肯定会拓宽我们的视野，可以从代数和几何两方面观察问题的基本特征，开发利用题目隐含（代数的或者几何的）的数学属性.把问题进行适当转换，往往能够强化我们对于问题解法的预见性，从而轻松获得问题的简洁解法.

例1 （1）如例1（1）图，F1，F2是双曲线的左、右焦点，过F1的直线l与双曲线的左右两支分别交于点A，B.若△ABF2为等边三角形，则双曲线的离心率为_________.

（2）如例1（2）图①，从双曲线的左焦点F引圆x2+y2=a2的切线，切点为T.延长FT交双曲线右支于P点，若M为线段FP的中点，O为坐标原点，c为双曲线的半焦距，则MO-MT等于（ ）.

A.c-b B.b-a C.a-b D.c-a

（3）F1、F2是双曲线的左、右焦点，点P在双曲线的右支上.则△PF1F2内切圆圆心的横坐标为（ ）.

A.c-b B.a C.b D.c

例1（1）图

例1（2）图①

探究：结合题目条件和几何图形，配合双曲线的定义和性质，发现解决问题的基本思路应该不难.

（1）假设等边三角形△ABF2的边长为m，可以将m标注在图形的三条边上.

由双曲线定义可得AF1-AF2=2a，所以AF1-AB=2a，所以BF1=2a.

又因为BF2-BF1=2a，所以BF2=4a.

所以△AF1F2的三条边长分别为6a，4a，2c.

由余弦定理可得：4c2=36a2+16a2-24a2，

所以，所以离心率

（2）取双曲线右焦点F'，连接PF'，MO，TO.

应该在图形上有所作为，注意向双曲线的定义和切线性质靠拢.

Rt△OFT中，由勾股定理可得TF=b，

MO为△PFF'的中位线

例1（2）图②

例1（3）图

（3）双曲线和△PF1F2及其内切圆如图所示，M，N，H为三个切点，圆心为I，结合图象可知这两个点H，I的横坐标相等.

设△PF1F2内切圆圆心I的横坐标x.

由内切圆的性质可得PF1-PF2=HF1-HF2，

所以2a=（x+c）-（c-x），所以x=a.

说明：结合图形和双曲线的定义，将图形充分的发展，其中发展条件的辅助线对获得问题的研究方向十分重要，配合以代数的方法（余弦定理勾股定理等等），问题的思路便十分凸显了，肯定会触发灵感的，获得成功几乎是一种必然.

例2 （1985年全国高考题）设a，b是两个实数，A={（x，y）|x=n，y=na+b，n∈Z}，B={（x，y）|x=m，y=3m2+15，m∈Z}，C={（x，y）|x2+y2≤144}，讨论A∩B≠φ与（a，b）∈C能否同时成立.

探究1：集合A，B都是不连续的点集，“存在a，b，使得A∩B≠φ”的含意就是存在整数m和n使得

由此得出，存在整数n使得na+b=3n2+15，也就是3n2-an-b+15=0.

这个关于n的方程有整数解，所以其判别式Δ=a2+12b-180≥0，

所以

它的几何意义就是一条抛物线的上方区域，如图所示.

例2图

又因为（a，b）∈C，所以要确保结论成立.结合图形可知，抛物线+15必须与圆a2+b2=144有交点.

联立方程组可得b2-12b+36=0，所以b=6，代回可得：

此时，B={（x，y）|x=m，y=3m2+15，m∈Z}.A中每个点的纵坐标都是无理数，B中每个点的纵坐标都是有理数，所以A∩B=φ，也就是A∩B≠φ与（a，b）∈C不能同时成立.

探究2：换一个角度观察na+b-（3n2+15）=0有解的问题.

这个等式表明点P（a，b）在直线L：nx+y-（3n2+15）=0上（n∈Z）再抓住参数a，b，则此问题的几何意义是动点（a，b）在直线L上，且动点（a，b）在圆x2+y2=144上或者内部.如果这两个条件相容的话，应该有圆心到直线距离d≤12.

因为n为整数，所以上式不能取等号.

这就得到了两个互相矛盾的结果，所以A∩B≠φ与（a，b）∈C不能同时成立.

说明：联想转化是一种重要的数学思想，在审题的过程中就应该进行相关的工作.如果是代数条件，就应该设想它的几何背景；如果是几何条件，就应该画出图形，在对应的图形上标注所有的代数信息.代数方法和几何方法结合起来，优劣可以立刻判断出来.在两种方法中间进行转换或者选择，我们的数学解题会变得游刃有余.

例3 从“三角形的三条高线交于一点”证明方法的变迁看数形结合的价值.

探究：这个问题从初中到高中，从1980年的高考题到现在高中选修课的课堂探究，处处能看到它的身影.题目未变，我们却一直在成长.从初中的相似三角形四点共圆一直到高中的坐标法向量法，都能完成这个问题，方法越来越简洁美妙，其中的主要功劳是知识的增长和方法的迭代，数形结合是其中的主要亮点.

探究1（纯粹的几何法）：已知：△ABC的两条高BE，CF相交于点O，第三条高AD交高BE于点Q，交高CF于点P.求证：P，Q，O三点重合.

如例3图①，有大大小小的直角三角形，没有全等只有相似，所以应该从发展相似三角形开始.

因为BE⊥AC，CF⊥AB，所以∠AEB=∠AFC=90°.

又因为∠BAE=∠CAF，所以△ABE∽△ACF，

所以，所以AB·AF=AC·AE.

又因为AD⊥BC，所以△AEQ∽△ADC，△AFP∽△ADB.

同样可得AC·AE=AD·AQ，AB·AF=AD·AP.

研究上面既有的成果，可以有新的进展，结合结论的要求证明三点重合，我们的目的可以更加明确.

因为AB·AF=AC·AE，AC·AE=AD·AQ，AB·AF=AD·AP，

所以AD·AQ=AD·AP，所以AQ=AP.

因为点Q，P都在线段AD上，所以点Q、P重合，

所以AD与BE，AD与CF交于同一点.因为两条不平行的直线只有一个交点，所以BE与CF也交于此点，所以点Q，P，O重合.

例3图①

探究2（纯粹的几何法还可以利用四点共圆的方法）：已知△ABC的两条高BE，CF相交于点O，连接AO并延长交BC于点D，求证：AD⊥BC.（略）

探究3（数形结合，坐标法）：进入高中后，坐标法成了我们更加有力的工具，直线方程直接把几何问题变成了代数计算，问题的思考方式变得单纯而简洁.

探究4（也可以用坐标向量证明两条高的交点在第三条高线上，这也是数形结合的主要方式）：如例3图②，以直线BC为x轴，高AD为y轴，建立直角坐标系.设A（0，a），B（b，0），C（c，0），设高线AD与BE交于G（0，m）.

可得

例3图②

，所以=0，所以CG⊥AB，

从而CG是AB边上的高线，故三高共点.

说明：到了高中，数形结合使得问题的证明变得异常简洁优美，几何问题转化成代数计算，问题变得单一且易于把控.

数形结合可以减少运算量，缩短思维链的长度，简化推理和论证的整个流程.

充分观察开发问题中的代数和几何两个方面的特征并加以利用，往往能够提升我们的洞察力，避免那些不必要的运算，优化问题的思维方式，提高解题的自觉意识和主动性.尤其在解选择题、填空题的时候，这种思想更显现其优越性.解题过程中要积极主动地开拓自己的思维视野.

例4 （1）若关于x的不等式x2-3ax+2a-6＜0，在-1＜x＜1时恒成立，求实数a的取值范围.

（2）设A={x|1＜x＜3}，B是关于x的不等式组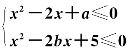的解集，试确定a、b的取值范围，使得A⊆B.

（3）若函数f（x）=mlnx+x2-mx在区间（0，+∞）内单调递增，则实数m的取值范围为（ ）.

A.[0,8] B.(0,8]

C.（- ∞,0］∪[8,+∞) D.(-∞,0)∪(8,+∞)

探究：（1）一元二次不等式的讨论常常可以借助于一元二次函数的图象，这样不仅可以避免那些烦琐的讨论，而且极有可能大大减少题目的运算量.

设f（x）=x2-3ax+2a-6（-1＜x＜1），如图所示.

只要让图象的两个端点不在x轴以上即可，问题等价于

例4图(www.xing528.com)

所以，所以-5≤a≤1.

（2）再接再厉，与刚才的思想方法完全同构：A⊆B的意思就是1＜x＜3的时候，的两个不等式都恒成立.本题的答案为a≤-3，b≥3.请放手一试.

（3）很明显，恒成立，

所以2x2-mx+m≥0对所有正数都成立.

设g（x）=2x2-mx+m.

依据上述要求画出g（x）的图象，可以发现抛物线在y轴上的截距为m，

所以m≥0此时其图象的对称轴，抛物线应该与x轴无交点或者只有一个交点，所以m2-8m≤0，

解得0≤m≤8，故选A.

说明：恒成立问题一般转化成函数的最大值最小值的讨论.函数的最值，在本题中还要对二次函数的对称轴与定义域的相对位置进行分类讨论.结合函数图象，有效地避开了这种烦琐的讨论，问题更容易理解和转化，思路清晰、运算简洁.

与二次函数、二次方程、二次不等式有关的问题，画出二次函数的图象，往往会产生意外的灵感.

例5 设M点在△ABC内部，且有，求△ABC的面积与△AMC的面积的比.

探究1（纯几何方法）：将MB延长一倍至B'，以MA，MB'为邻边做平行四边形AMB'E，ME与AB交于D点.

由△ADE∽△BDM，而且相似比为2∶1，

所以ED=2DM，进而

例5图①

所以，所以M为CD的中点.

过D做DF⊥AC于点F，过B做BG⊥AC于G，过M做MH⊥AC于H.

△ABC的面积与△AMC的面积的比为BG∶MH.

在△ABG中，DF∶BG=2∶3；在△CDF中，MH∶DF=1∶2，

所以BG∶MH=3，所以△ABC的面积与△AMC的面积的比为3∶1.

说明：这个问题，如果改变其中的系数，难度肯定还要加大，而且每个问题的方法都不尽相同，辅助线也太多了，乱花渐欲迷人眼，真有些招架不住了.

探究2：坐标法是笛卡尔的发明，很多问题在坐标系里面都变成了单纯的计算问题，这就大大缩短了我们思维链的长度，同时也大大降低了运算量！为此，可以考虑向量问题坐标化.

以A为坐标原点，AC为x轴建立直角坐标系，设C（b，0），B（a，c），M（x，y），则

例5图②

△ABC的面积与△AMC的面积的比为B点与M点的纵坐标之比.

由可得-y+2c-2y-3y=0，

即

说明：多么简洁优美的方法，这完全得益于数形结合，而且改变题目中向量的系数，思路程序运算量完全一样，完全不用再去想破脑袋了.这个结论就是著名的“奔驰定理”.

若O为△ABC内任意一点，则

如果用数形结合的坐标法证明奔驰定理，会比网络上的其他证明方法简洁许多.

设M点在△ABC内部，且有0，则△BMC，△AMC，△AMB，△ABC的面积之比为1∶2∶3∶6.这是奔驰定理的直接解读.

奔驰定理因为此类问题的图形与奔驰汽车的Logo相似而得名.

例5图

例6 （1）定义域为[a，b]（a，b∈Z），值域为[0，1]，那么满足条件的有序实数（a，b）共有（ ）.

A.3对 B.4对 C.5对 D.9对

探究：这是一个偶函数，当x≥0时，，函数图象是的图象左移两个单位再下移一个单位后的结果.

如例6（1）图，

例6（1）图

点A，E是图象的最低点，点C是图象的最高点，要确保函数的最大值为1、最小值为0.又因为定义域的端点都是整数，定义域内的图象可以是A，C之间，A，D之间，A，E之间，B，E之间，C，E之间，所以有序实数对（a，b）共有5对.

另外，两种重要的数学思想：等价转化与数形结合，它们可以密切配合一下，问题会变得更加优美.

的值域可以变成的值域，进而变成y=的值域，最后变成甚至y=|x|的值域.你试试呗.数学需要体验，亲自体验，心情会更爽.

（2）A（cosα，sinα），，则A与B的距离为_________.

探究：最正统的方法当然是利用两点间的距离公式和两角和的正弦余弦公式，运算量比较大，正难则反，联想三角函数的定义可以发现：

|OA|=|OB|=1，∠AOB=60°，所以△AOB为等边三角形，所以|AB|=1.

（3）设等差数列{an}的前n项和为Sn，S12＞0，S13＜0，则S1，S2，…，S12中的最大值为_________.

探究：直接研究Sn的函数表达式，显然运算量思维链的长度都较大.将结论和条件兼顾可以使我们联想到，等差数列的前n项和公式为n的二次函数，而且没有常数项，也就是其图象必过原点；又因为S12＞0、S13＜0，所以该函数的另外一个零点介于12和13之间.如例6（3）图所示，函数图象的对称轴应该等于两个零点的平均数，它介于6和6.5之间；又因为n为整数，所以再一次结合图象可得S6最大.

例6（3）图

例6（4）图

（4）求函数的最大值最小值.

探究：利用均值不等式得f（x）=（当且仅当……），函数的最大值为.因为该函数在定义域内连续，所以必定存在最大值最小值；又该函数为奇函数，其最大值最小值是一对相反数，所以函数的最小值为

你能画出该函数的图象吗？它有几个关键点？它们的参照作用非常重要！

说明：解答本例题的4个小题，都是将函数问题转化为对图象的研究，思路清晰，几乎不用运算就获得了答案，图形的直观性和先进性得到了完美的体现.在数形之间产生联想并且进行转化，是一种重要的数学思想，它应该成为我们研究数学问题的自觉意识.

数形结合可以深刻理解数学问题的本质，真正形成数学能力.

数形结合可以让我们全方位地理解和分析数学问题，在数形两个方面对数学问题进行相互印证，对其中的知识与方法的感知会更加真切、理解会更加深刻、记忆也会更加久远.

例7 （1）函数y=x2-2x+3的定义域为[a，b]，值域为[2，3]，则b-a的最大值最小值分别是_________.

探究：如例7（1）图，A（0，3），B（1，2），C（2，3），点B是图象的最低点，要确保函数的最大值为3、最小值为2，定义域内的图象至少是A，B之间或者B，C之间，至多是A，C之间，所以b-a的最大值最小值分别是2和1.

（2）函数y=|log2x|的定义域为[a，b]，值域为[0，1]，则b-a的最大值最小值分别是_________.

探究：如例7（2）图，，B（1，0），C（2，1），点B是图象的最低点，要确保函数的最大值为1最小值为0，定义域内的图象至少是A，B之间，至多是A，C之间，所以b-a的最大值最小值分别是.和

例7（1）图

例7（2）图

（3）函数y=sinx的定义域为[a，b]，值域为，则b-a的最大值最小值分别是_________.

探究：如例7（3）图，，点B是图象的最低点，要确保函数的最大值为，最小值为-1，定义域内的图象至少是A，B之间或者B，C之间，至多是A，C之间，所以b-a的最大值最小值分别是和.

例7（3）图

（4）已知，若存在实数b，使两个函数y=f（x）与y=b的图象有两个零点，则a的取值范围是________.

探究：这是一个分段函数，也需要对定义域进行分类讨论.

题目要求函数y=f（x）的图象与y=b这样的直线有两个交点.

①若a＜0，则a3＜a2，函数y=f（x）图象如例7（4）图①所示，点A高于点O显然可以满足条件要求.

②若0≤a≤1则a3≤a2，函数y=f（x）图象如例7（4）图②所示，点A高于点B，显然不满足条件要求.

③若a＞1，则a3＞a2函数y=f（x）图象如例7（4）图③所示，点A低于点B，显然可以满足条件要求.

所以，a的取值范围是a＜0或者a＞1.

例7（4）图①

例7（4）图②

例7（4）图③

说明：上述四个问题的共同特征是函数表达式是确定的，但是定义域在变化，题目要求根据函数的某种特性确定定义域的各种可能性.研究方法都是数形结合，充分运用变量思维；画出函数“完整图象”，让函数的定义域充分地动态变化.在动态的变化过程中，我们可以发现其中的变化规律，找到符合问题要求的“临界点”，在此基础上问题往往能够顺利解决.

以上问题中，数形结合、分类讨论与动态分析综合在解答过程中.对此，我们可以更加深切地感受到数形结合的魅力，也更加深刻地理解了变量思想，其中定义域的变化和动态分析对函数性质的影响和发现有着不可估量的作用.在这些问题的研究过程中，基础知识不断被夯实，思想方法逐步被强化，数学问题的研究能力稳步提高.