函数与方程是两个不同的概念,但它们之间有着密切的联系,方程f(x)=0的解就是函数y=f(x)的零点,函数y=f(x)也可以看作二元方程f(x)-y=0,通过方程进行研究.两种思想方法是相辅相成的.有关方程、不等式、最值等问题,利用函数与方程观点加以分析,可以使问题更加明朗,从而易于找到适当的解题途径.
函数思想与方程思想在一定的条件下是可以相互转化的,是相辅相成的.函数思想重在对问题进行动态的分析研究,方程思想则是在动中求静,研究系统中各种元素间的等量关系.函数与方程是一般和特殊的关系,把二者结合起来研究和处理数学问题,这就是函数与方程思想.
以函数与方程思想研究数学问题主要有以下三个方面.
(一)把函数问题和方程问题相互转化,当研究方程问题遇到困难时往往将其转化为函数问题,反之亦然
这其实就是等价转化思想的特殊表现形式.它山之石可以攻玉.直接研究某种问题遇到困难的时候,将其适当转化,新的情境往往带给我们全新的视野.这种背景下,最容易产生创新和突破.
例25 (1)关于x的方程9x+(4+a)3x+4=0恒有解,求a的取值范围;
(2)方程3x2+2(k-1)x+k+5=0在区间(0,2)内有解,求k的取值范围;
(3)已知关于x的方程x2-2cosx+a2=0有解,求a的取值范围.
探究:(1)方法1:设3x=t,则t>0.原方程有解即方程t2+(4+a)t+4=0有正根.
即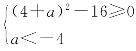 ,所以
,所以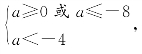
解得a≤-8.
方法2:设f(t)=t2+(4+a)t+4.
①当Δ=0时,即(4+a)2-16=0,所以a=0或a=-8.
a=0时,f(t)=(t+2)2=0,得t=-2<0,不符合题意;
a=-8时,f(t)=(t-2)2=0,得t=2>0,符合题意,
所以a=-8.
②Δ>0,即a<-8,或a>0时,因为f(0)=4,故只需对称轴![]() 0,即a<-4,所以a<-8.
0,即a<-4,所以a<-8.
综上可得a≤-8.
(2)这个问题当然可以像上一小题那样,结合二次函数图象,分类讨论对应二次函数的判别式、对称轴的范围、端点函数值的符号,但是那样太过烦琐,转化成函数问题可能会有转机.
由原方程可得:
3x2-2x+5+(2x+1)k=0,
显然,2x+1不可能为零,
所以![]()
令2x+1=t,t∈(1,5),则![]()
令![]()
k的取值范围就成了这个函数的值域,
这是一个常见的“对号函数”:
k∈(-5,-2].
(3)方法1:这个方程难以求解,只能借助于函数这个工具.
令f(x)=x2-2cosx+a2.
因为f(-x)=f(x),
所以f(x)是偶函数,
所以f(x)的图象关于y轴对称.
f'(x)=2x+2sinx.
结果还是不甚理想,但是f″(x)=2(1+cosx)≥0,
所以f'(x)为增函数.又f'(0)=0,
所以x>0时,f'(x)>0;x<0时,f'(x)<0,
所以x>0时,f(x)单调递增,x<0时,f(x)单调递减,
所以函数f(x)的最小值为f(0)=-2+a2.
结合函数的图象可知原方程有解等价于:
f(0)=-2+a2≤0,所以![]()
![]()
方法2:可以把原方程有解转化成两个函数图象y=x2+a2与y=2cos x,有交点的问题,如图所示,显然应该有a2≤2,所以![]()
例25图
说明:不能直接求解的方程问题,往往转化为函数问题.如果有时候一个函数难以研究甚至要转化成两个函数的问题.通过对对应函数对称性单调性极值点及最值的分析研究,借助函数这个强大的工具,我们对方程会有更加全面的认识,常常可使问题“拨云见日”.
对于含参方程,通常有三类解法:一是换元,将问题转化为二次方程,利用根与系数的关系或判别式,或者利用三角函数的有界性加以解决;二是分离变量构造函数,把方程有解转化为求函数的值域,再根据函数的图象和性质来解决;三是直接把方程问题转化为对应函数的零点问题,利用初等函数甚至导数的方法来研究.
例26 (1)关于x的方程ex-x+k=0有两个不等实根,求实数k的取值范围.
(2)关于x的方程![]() 有实数根,求实数k的取值范围.
有实数根,求实数k的取值范围.
探究:(1)不会解的方程当然要转化成函数问题.
假设f(x)=ex-x+k,它的零点就是原方程的根,由题意可知它有两个零点.
f'(x)=ex-1.
显然x>0时,f'(x)>0,f(x)单调递增;x<0时,f'(x)<0,f(x)单调递减.f(x)最小值为f(0)=k+1.
结合函数图象可得k+1<0,所以k<-1.
例26(1)图
例26(2)图
(2)显然,我们不会解这个方程,只能转化为函数问题.和上题不同的是:该题应该转化为两个函数问题,因为如果变成一个函数,可能太过复杂,
也就是函数![]() 与函数g(x)=ex-1+e1-x+k的图象有交点.
与函数g(x)=ex-1+e1-x+k的图象有交点.
因为![]() ,所以当x∈(0,1)时,f'(x)>0;当x∈(1,+∞)时,f'(x)<0,(https://www.xing528.com)
,所以当x∈(0,1)时,f'(x)>0;当x∈(1,+∞)时,f'(x)<0,(https://www.xing528.com)
所以函数f(x)在区间(0,1)上为增函数,在区间(1,+∞)为减函数,
所以函数f(x)的最大值为f(1)=1.g'(x)=ex-1-e1-x.
显然,x>1时,g'(x)>0,g(x)为增函数;x<1时,g'(x)<0,g(x)为减函数.
所以,当x=1时,函数g(x)取得最小值为g(1)=k+2.两个函数的极值点是相同的.结合两个函数的图象可知,二者有交点等价于k+2≤1,即k≤-1,所以实数k的取值范围是k≤-1.
说明:对不会解的方程一般都可转化成函数问题,结合函数的导数、单调性、奇偶性、极值与最值和函数图象,问题一般都能顺利解决.但是,方程转化为一个函数还是两个函数,需要我们认真研究方程结构,确定所选函数的研究难度.
(二)函数与方程的结合问题
在研究函数的时候,需要构建方程去沟通函数中的各种变量间的关系,使得函数更明确更简洁,在研究方程的时候,利用函数性质去研究方程中各种未知数的相互依存关系.
在很多综合问题中,往往不是单一的研究方程或者函数,而是将二者结合起来,二者可能互为因果、相互补充、交叉推算.
函数与方程的思想也是高考的考查重点,主要考查内容如下.
1.求函数的最值或参数的取值范围.
2.已知方程的特定解,求其中参数的取值范围,一是分离参数构建函数,将方程有解转化为求函数的值域;二是换元,将复杂方程问题转化为熟悉的二次方程,进而利用二次方程解的分布情况构建不等式(组)或构造函数加以解决;三是直接把方程问题转化为对应函数的零点问题.
3.不等式恒成立能成立问题,其方法就是构造适当的函数利用函数的图象和性质解决问题.
4.最优化问题.
5.解析几何问题:直线和圆锥曲线的交点问题,经常要转化为方程问题,用方程的理论加以解决,包括联立方程组、结合韦达定理和弦长公式在发展条件中构建方程、在消元之后优化函数、最终完成函数的研究或者是方程的求解.
例27 (1997年全国高考题)设圆满足:①截y轴所得弦长为2;②被x轴分成两段圆弧,其弧长的比为3∶1,在满足条件①②的所有圆中,求圆心到直线l:x-2y=0的距离最小的圆的方程.
探究:看结论解答此题一般考虑待定系数法,前两个条件可以得到两个方程,而第三个条件应该构建目标函数进行研究.函数与方程是该题的主要考查目标.
如图:
设圆心为P(a,b),半径为r,则点P到x轴,y轴的距离分别为|b|,|a|.
设圆与y轴的两个交点为A,B,圆与x轴的两个交点为C,D.
圆P截y轴所得的弦长为2,所以在等腰三角形PAB中,由弦长为2弦心距为|a|可得r2=a2+1.从而得r2-a2=1.……①
因为圆P被x轴分成两段弧长的比为3∶1,所以圆P截x轴所得劣弧对的圆心角为90°,在等腰直角三角形PCD中,易得弦长为![]()
例27图
由①②可得2b2-a2=1.……③
又点P(a,b)到直线x-2y=0的距离为![]()
要研究该函数的最小值,最大障碍是其中的两个自变量和绝对值符号,两个自变量a,b满足③的平方关系.
所以5d2=|a-2b|2=a2+4b2-4ab.
面对这个结构,基本不等式是一种试探方向.
5d2=a2+4b2-4ab≥a2+4b2-2(a2+b2)≥2b2-a2=1.
当且仅当a=b时上式等号成立,此时5d2=1,从而d取得最小值.
由此由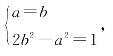
得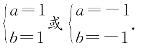
由于r2=2b2知![]() 于是,所求圆的方程是:
于是,所求圆的方程是:
(x-1)2+(y-1)2=2,或(x+1)2+(y+1)2=2.
说明:本题解法又是函数与方程思想的集中体现,通过方程沟通变量之间的联系,见缝插针地实行消元,然后通过对目标函数两边平方的方法,使之与条件③(2b2-a2=1)建立形式上的联系(二者都是平方关系),最后一步使用基本不等式获得一个定值的结论,完成了最后的穿越.这看似偶然,实则必然.
事实上,对4ab还有多种变换方式.比如,![]() ,总有一款能和条件③(2b2-a2=1)完成对接而得到一个常数.
,总有一款能和条件③(2b2-a2=1)完成对接而得到一个常数.
该题最后求解的是方程,但是中间函数的最值研究最为关键.这是函数服务于方程的范例,下面的问题也是这样的.
例28 椭圆中心在原点,焦点在x轴上,离心率为![]() ,动直线与以原点为圆心,椭圆短半轴为半径的圆相切,该直线与椭圆交成线段的最大长度为4,求椭圆的方程.
,动直线与以原点为圆心,椭圆短半轴为半径的圆相切,该直线与椭圆交成线段的最大长度为4,求椭圆的方程.
探究:求椭圆的方程只能用待定系数法.
设椭圆方程为![]()
离心率为![]() ,所以
,所以![]() ,所以a2=4b2.
,所以a2=4b2.
椭圆方程可设为![]() ,即x2+4y2=4b2,圆的方程为x2+y2=b2.
,即x2+4y2=4b2,圆的方程为x2+y2=b2.
假设切线方程为y=kx+m,所以圆心到切线的距离![]()
所以m2=b2(1+k2).……①
将直线方程和椭圆方程联立可得:
(1+4k2)x2+8kmx+4m2-4b2=0.
假设两个交点A(x1,y1)B(x2,y2),
将①代入得:
令1+4k2=t(t≥1),可得![]()
由二次函数的性质可得:
当![]() 即t=3时,|AB|取得最大值2b,所以2b=4,b=2,
即t=3时,|AB|取得最大值2b,所以2b=4,b=2,
所以椭圆的方程为![]()
说明:在高中数学里,考查运算能力的最高点就是解析几何,明确运算目标、选择运算途径、简化运算过程都是对数学能力的较高要求;而要完成这样的目标,将函数与方程结合起来,二者相辅相成,解决问题的基调便得以确立.
本题里,还是发展条件、得到方程、利用方程完成函数研究中迫切需要的消元;另外,配凑法和换元法也是函数研究中的常见方法.
总之,函数与方程是数学研究中的两位“战神”,它们都有着自己的知识背景和使用范围,但在很多情况下都可以相互转化.当方程的问题遇上函数的方法,问题可能变得非常轻松,反之也是如此.如果同一个问题用上函数与方程两种知识和方法,我们的研究会如虎添翼.
函数与方程是我们研究数学问题的首选,在数学探索处于困顿的时候,它能给我们带来一片光明,使我们的研究有章可循、有法可依,使对数学问题的成功探索几乎成为一种必然.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




