高中数学思想方法-方程思想的重要性

方程思想，是将问题要素之间的各种关系转化为方程（组），然后通过解方程（组）来获得问题的解决.许多问题中含有常量、变量和参量，可以通过适当方式，运用方程的观点去观察、分析问题的结构特点，抓住某一个关键未知量（主元），并以其为核心构造和处理上述方程.

利用方程解题不外下述三个步骤：首先是将数学问题转化为方程问题，构建常见的方程或方程组；其次是运用方程的性质求解或讨论；最后将由方程得到的结论返回到原来的问题中，还原问题的答案.

构建方程的意识和利用方程性质求解的技能，常常是问题解决过程中的核心.

方程思想是解决数学问题的重要思想之一，也是常用方法之一.在三角函数、数列、解析几何等中常用方程来解决.解方程的主要方法有配方法、换元法、加减消元法、代入消元法、平方相加法等.

例12 如果从1985年开始，我国每一年的GDP都比上一年平均增加8%，试问：至少要经过多少年我国当年的GDP能翻两番？（参考数据：lg2=0.30，lg3=0.48）

探究：“我国当年的GDP翻了两番.”这句话的信息就是方程.

“翻番”的概念：折叠一张厚度为1的白纸，第一次折叠（翻一番）后，纸张厚度为2，第二次折叠（翻两番）后，纸张厚度为4，第三次折叠（翻三番）后，纸张厚度为8……“翻n番”的意思就是变成了原来的2n倍.

假设经过n年，我国当年的GDP能翻两番，即（1+8%）n=4，

所以1.08n=4（根据题给数据，应该将其转化成常用对数，力求变成lg2和lg3的结构），

所以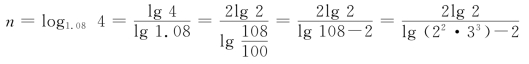

将数据代入可得n=15，即15年后我国当年的GDP会翻两番.

说明：将应用题转化成数学题的过程就是构建一个方程，它把所有的关系都集中起来了.

在对数转化的过程中，注意向着可用数据的方向发展，一切都变成lg2和lg3的形式.充分使用条件，让每一个条件都能发挥作用，是一个基本的解题原则.

例13 某地发生泥石流，需要当地所有挖掘机抢险救灾，所有挖掘机的工作效率是相同的.若这些挖掘机同时工作，24小时即可完成.但它们实际上是间隔相同的时间，从不同的地点陆续赶来，顺序投入工作的，且一旦投入，就一直进行至工作结束.已知第一台挖掘机的工作时间是最后一台的5倍，试求这项工作自始至终持续了多长时间.

探究：本题信息量较大.综合起来看，“若这些挖掘机同时工作，24小时即可完成”和“第一台挖掘机的工作时间是最后一台的5倍”都蕴含着等量关系，把它们变成方程，问题基本上就搞定了.

假设当地一共有n台挖掘机，若同时工作，累计时间为24n.

假设它们实际工作时间分别为a1，a2，a3，…，an，显然这是一个等差数列，所以a1+a2+a3+…+an=24n，所以，所以a1+an=48.

又a1=5an，所以6an=48，所以an=8，所以a1=40；也就是说，抢险救灾工作历时40小时.

说明：本题实际上是建立了一个方程组，建立了一个独立的“生态环境”.在这个环境内，问题要素（a1，an，n）之间形成了一种天然的制约关系（方程组）.

该题解法精妙，令人振奋；看似偶然，实则必然.

引进字母，把应用题转化成纯数学问题，我们的思路就会慢慢走向正轨.在方程组的研究过程中，充分使用等差数列的条件和特性，也是解答本题的关键之一.

例14 如图，∠ABC=90°，，BC=1，P为△ABC内一点，∠BPC=90°.（1）若，求PA；（2）若∠APB=150°，求tan∠PBA.

探究：Rt△ABC已经完全确定，这是一个组合图形，要求哪个元素，就应该在该元素所在的三角形内，或者直接求解，或者向相邻的三角形扩张求援，充分利用所有条件，尤其是那两个直角三角形，建立相应的方程或者方程组.

例14图

（1）Rt△PBC中，因为BC=1，，所以∠CBP=60°，所以∠PBA=30°.△PAB中，由余弦定理得：

（2）设∠PBA=α，△PAB中，∠PAB=30°-α.

要求tanα，应该把所有的角都有α表示，最终得到关于α三角函数的方程.

Rt△PBC中，∠PBC=90°-α，∠PCB=α，又因为BC=1，所以PB=sinα.

回到△PAB中，由正弦定理得

化简得，故

说明：只要把条件和结论的各种元素纳入方程之中，它们的关系就比较容易把控了.

几何问题，尤其是组合类图形，在研究过程当中，务必要扩大视野.在目标图形上求解某一元素遇到困难时，可以转化到相邻的图形内去寻找新的思路增长点.

例15 （1）已知θ为锐角，且，则

（2）锐角θ，φ，使得且为偶函数，求θ，φ的值.

探究：（1）条件就是一个方程，可以先去化简它，希望能发现有利于结论的信息.

因为cos3θ=cos（θ+2θ）=cosθcos2θ-sinθsin2θ

=cosθ(2cos2θ-1)-sinθ×2sinθcosθ

=4cos3θ-3cosθ，

可得sin3θ=3sinθ-4sin3θ.

因为，所以

所以

则

说明：三倍角公式也不是什么禁区，在方程的大环境里大胆发展，问题可能没有你想象得那么难.

（2）要考察函数的奇偶性，就应该将f（x）与f（-x）的表达式进行比对.

，此时只有x是变量，其他的都是常数.

由f（x）=f（-x）可得对任意x恒成立，所以，又因为

所以，两式平方相加可得，容易得到，进而.

说明：发展条件，转化结论，瞻前顾后，我们的解题探索会左右逢源.

要求两个未知数，除了题目给出的那个方程之外，我们还应该去寻找另一个关于它们的方程.

平方相加是三角函数中的常规消元方法，它能有效地引入新的制约机制.其实，cos2φ+sin2φ=1就是增加了一个条件，增加了一个新的方程，这就是平方相加消元的最好解释.

利用方程思想研究数学问题，要注意以下四点.

（一）坐标系与方程组

坐标系的发明，使得很多证明和计算都可以变成方程或方程组，这当然也包括用坐标法证明平面几何问题，其实就是方程思想的集中体现.坐标法不仅思路稳定，而且只要设计合理运筹得当，计算也很简单.

例16 三个圆两两相交，有三条不平行的公共弦，判断它们所在直线的位置关系并证明.

探究：这是一道初中数学竞赛试题，难度较大.但是到了高中，我们学习了直线和圆的方程，利用方程思想处理该问题，或许会曲径通幽.

假设三个圆的方程分别为：

①-②，②-③，①-③可以分别得到三条公共弦所在直线的方程：

联立方程组，求出三条交线的交点坐标，难度很大.

面对这种复杂的结构，还是那种既定的思路：观察分析这种“大块头”的结构特点，希望从中发现规律性的信息.

观察上面三条直线方程的结构可以发现：

④+⑤=⑥.

这说明若l1和l2的交点坐标（x0，y0）满足④和⑤，

则它必定满足⑥，即（x0，y0）也在l3上，

也就是三条公共弦所在直线相交于一点.

说明：请看，利用方程思想对问题进行转化会获得多么美妙的解答.当然，在这其中，对方程的宏观结构特征进行观察分析，巧妙地避开了解方程组的烦琐计算也非常重要.

方程组就是一张大网，它几乎构建了问题要素之间的全部联系.“方程恢恢疏而不漏”，方程组一旦建立，不经意间就可能完成一次转化或者跨越.

该题里，我们没有刻意地去建立特殊的坐标系，目的是让三个圆的方程呈现相似的结构.这种对称和相似的结构.在后来的表述当中条理清晰、结构统一，为我们的观察和理解带来了极大的便利.

例17 （1984年高考试题）在△ABC中，∠A，∠B，∠C所对的边分别为a，b，c，且c=10，P为△ABC的内切圆上的动点.求点P到顶点A，B，C的距离的平方和的最大值与最小值.

探究：这是当年高考的第七题，1984年高考数学试题是有史以来最难的试题.

由正弦定理得

整理得cosA×sinA=cosB×sinB，即sin2A=sin2B，

则2A=2B或2A=π-2B.

因为，所以2A=2B舍去，

所以

△ABC为Rt三角形，

a=6，b=8，

（用等面积法求三角形的内切圆半径更是通性通法，以内切圆心为顶点，以三角形的三条边为底边，可以构成三个三角形，它们的高都是内切圆的半径，它们的面积之和等于原三角形的面积）

以CA，CB为坐标轴建立坐标系.设△ABC各顶点的坐标为C（0，0），A（8，0），B（0，6），则内切圆圆心M（2，2），内切圆方程为（x-2）2+（y-2）2=4（0≤x≤4），

也就是x2+y2-4x-4y+4=0，（x2+y2=4x+4y-4）；也可以是参数方程形式：

例17图

x=2+2cosα，y=2+2sinα.

设点P到各顶点A，B，C的距离的平方和为s，则：

s=x2+y2+(x-8)2+y2+x2+(y-6)2

=3（x2+y2-4x-4y）-4x+100（把x2+y2换成4x+4y-4也可以，也是一种化简——降次）

=3×(-4)-4x+100

=88-4x(0≤x≤4).

x=0和x=4的时候，所求最大值最小值分别为88和72.

另外，如果将参数方程代入：

s=x2+y2+(x-8)2+y2+x2+(y-6)2，

更容易得到S=80-8cosα，

也容易求得所求最大值最小值分别为88和72.

说明：在方程中蕴含着很多信息（对应的边和角不等且有一定的比例关系），也有很多化简方法.用余弦定理同化为边或者用正弦定理同化为角，都是可以的.相比来说，后者更简练.通过对这个方程的连续发展，我们获得了△ABC的所有信息.

看到结论，我们还是能够想到那个几乎不变的思想——函数思想，但是坐标法给我们建立各种联系以更加广阔的视野.求出圆的方程之后，问题内部的联系变得更加明显了；最后无论是消元的参数方程法还是整体代换的降次，都是常用的化简手段.

谁也不会预见到最后的化简结果，不仅只有一个变量，而且还是一次的.“阳光总在风雨后”，数学问题的研究也往往会带给我们意外的惊喜.

（二）选择合适的未知数

列方程时，力求充分使用题目条件的特殊性，力求所列方程简洁明快，在列方程的起步阶段，就为解方程做好准备.这其中最重要的一点就是选择那些能够简单直接的未知数，有时候它们甚至不能直接表示结论，但是它们可以建立起条件和结论间的直接联系.

例18 设{an}是等差数列.已知，b1b2b3=.求等差数列{an}的通项.

探究：求等差数列{an}的通项an，就应该将条件转化成{an}的形式，也就是：

现在问题的核心就是求解该方程组，那么，未知数如何设定呢？

等差数列的连续三项往往可以设为a1=x-d，a2=x，a3=x+d.

这种设计自动完成了前三项的直接联系，而且这种对称的结构，容易在运算当中产生约分抵消等化简结果.这样一来，上述方程可化为：

进而，即

令2d=t可以整理得到4t2-17t+4=0，

所以t=4或，所以d=±2.

综合以上信息可得d=2时，a1=-1，an=2n-3；

d=-2时，a1=3，an=-2n+5.

说明：最后的方程里面，巧妙地选择未知数为后来的解方程带来了较大方便.一般来说，等比数列的连续三项可以设置为，x，xq.这种设置在研究它们的乘积时会很快约分.

总之，列方程（组）的时候，不能仅仅考虑当前的操作，还要为后续的解方程组做好铺垫，要条件结论兼顾，尽量利用题目条件结论的特殊性，在通性通法的基础上将问题进一步优化.(www.xing528.com)

（三）“设而不求”

“设而不求”是数学解题中的一种很有用的手段.采用“设而不求”的策略，往往能避开那些不必要的繁难的运算而直达目标.

整体代入是设而不求的一种方式.在解决某些多元方程问题时，要有目标意识，通过虚设的字母，绕开复杂的运算过程，整体转化至最终目标.

恰当合理地引入参数，通过参数建立方程，可使解题目标更加明确，条件和结论之间的联系更加明朗，这个参数最终可以消去不必解出而不影响结果.

例19 （1）函数y=3cosx的图象与y=4sinx的图象的交点为P，求点P到x轴的距离.

（2）函数y=6cosx的图象与y=5tanx的图象的交点为P，求点P到x轴的距离.

探究：（1）由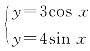得3cosx=4sinx，

两边平方可得9cos2x=16sin2x，

所以9（1-sin2x）=16sin2x，

所以

此时的x就是交点的横坐标，所以代入原函数表达式中得交点的纵坐标

所以两个函数图象交点到x轴的距离为

（2）由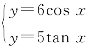得6cosx=5tanx，

所以6cosx=

所以6cos2x=5sinx，

所以6（1-sin2x）=5sinx，

所以6sin2x+5sinx-6=0，

所以（舍去）或

所以

此时的x就是交点的横坐标，所以代入原函数表达式中得交点的纵坐标

所以两个函数图象交点到x轴的距离为

说明：两个函数表达式里面的x和y都是变量，但是联立方程组之后，它们就都变成了定值，也就是交点的坐标，函数与方程在不知不觉间完成了转化，条件也就顺利地过渡到了结论.

研究方程组，我们并没有直接求出x，而是求出其某一种三角函数值，然后通过三角函数间的关系，整体代入而求出最终函数值.两个小题里面都没有把交点的横坐标求出来，尤其是第（2）小题，采用了设而不求的运算技巧，直接跳到了结论.

例20 在平面直角坐标系中，O（0，0），P（6，8），将向量按逆时针旋转后，得向量，则点Q的坐标是（ ）.

A.

B.

C.

D.

例20图

探究：因为，设以OP为终边的角为θ，

则

其中，

设Q（x，y），则向量，这是旋转后的向量，结合图形可得：

所以A选项是正确的.

说明：“设而不求”的计算技巧，不仅仅体现在解析几何中，在该题里面也体现得淋漓尽致.同时我们还可以发现，回归到三角函数的定义往往更容易发现问题的本质.

解析几何问题中，对于有关点的坐标问题、直线和圆锥曲线位置计算问题，“设而不求”都能促使问题定向，简便化归，收到以简驭繁的解题效果.

“设而不求”在研究曲线交点问题尤其是圆锥曲线问题时应用最为普遍.

例21 （1）过点P（1，0）的直线l与抛物线y=x2交于两点A，B，抛物线在这两点处的切线互相垂直，求直线l的方程.

（2）圆O的方程为x2+y2=r2，过圆外一点P（a，b）引圆的两条切线，切点分别为A，B，求直线AB的方程.

探究：（1）如例21图①：

例21图①

依据点斜式，可设直线的方程为：y=k（x-1），带入抛物线方程中得x2-kx+k=0.

假设两个交点A（x1，y1）B（x2，y2），则x1+x2=k，x1x2=k.

因为y'=2x，

所以A，B两点的切线斜率分别为k1=2x1，k2=2x2.

因为两条切线互相垂直，所以k1k2=4x1x2=-1，4k=-1，所以k=

所以直线l的方程为

（2）如例21图②：

此情此景，我们的困惑是两个切点的坐标太难求解了.可否通过设而不求的方法，避开这个复杂的运算呢？

我们的相关知识储备有将两个圆的方程做差可得它们公共弦所在直线的方程；圆O（x2+y2=r2）在切点A（x1，y1）和B（x2，y2）的切线方程分别为x1x+y1y=r2和x2x+y2y=r2.

例21图②

我们采用最后一条启发.

因为两条切线均过P（a，b），

所以ax1+by1=r2和ax2+by2=r2.

这是两个多么一致的结构！

这说明A（x1，y1）和B（x2，y2）均在直线ax+by=r2上，而过这两点的直线是唯一的，所以直线AB的方程就是ax+by=r2.

说明：大胆地引进字母，通过这些字母去建立方程，在发展和转化的过程中巧妙地避开了解方程组的复杂运算，这都是得益于我们对结论的深刻分析.在发展的过程中，我们始终关注结论的需要，将主要精力放在终极目标上，链条被一个个打开.越过“沙丘”结论正在等候.

另外，关注到两条切线长度相等，，而以P为圆心以切线长为半径的圆，与已知圆的公共弦即为AB，两个圆的方程作差可得直线AB的方程.你试一下呗！

例22 抛物线y=x2的一条动弦AB的长度为2，求AB的中点到x轴的最短距离.

探究：如图：

例22图

看结论就知道应该构建AB的中点M到x轴距离的目标函数，看条件应该联想到联立直线和抛物线的方程，二者的结合处可能就是该问题的突破点.

假设直线AB方程为y=kx+b，代入y=x2可得x2-kx-b=0.（k和b的引入，最初目的就是发展条件，将问题引入直线和圆锥曲线关系常规方法的轨道，并不一定去真正的求解它们，下面的两个交点A、B的坐标也是如此）

假设两个交点A（x1，y1）B（x2，y2），则x1+x2=k，x1x2=-b.

所以（1+k2）（k2+4b）=4，所以

（让消元成为一种习惯，k，b是我们自己引进的两个参变量，这样一来我们就得到了它们之间的直接联系）

转身再来研究结论.因为且M在直线y=kx+b上，

所以

M到x轴的距离

（这就是我们开始提出的目标函数，下一步是研究其最小值，观察函数的表达式结构，可以看出基本不等式可能是最佳选择）

配凑一下：

当且仅当即的时候，M到x轴的最小距离为

说明：本题在发展条件的时候体现的是方程思想，是解析几何问题的一般思路：联立方程组，韦达定理，弦长公式.值得一提的是消元思想，依据开始引入的两个参变数满足的方程，用k来表示b，为后期的发展提供了方便.

在研究结论M纵坐标的时候，我们是结合韦达定理得到横坐标后，代入直线方程得到纵坐标的，这也是常用方法之一，运算量一般比我们的想象要小很多.

最后把函数表达式配凑出基本不等式结构，也是一个常用技巧，基本原则是让函数表达式中的两个式子之积为定值，然后再配平整体.

在圆锥曲线问题中，设交点坐标而不求几乎是一种通法，这样的问题很多很多.

（四）千方百计地将目标元素（结论要求）“嵌入”条件方程内

发展条件的时候，有意识地将结论元素纳入方程组内.在发展条件的时候，要具备消元的自觉意识，力求嵌入目标元素而消掉其他元素.这一点看似顺理成章，但是在解题过程当中，往往不易保持清醒的头脑而乱了方寸.所以在研究中，一定要时刻关注我们的终极目标，做到每一步发展都更靠近结论.

例23 △ABC中，角A，B，C所对的边分别是a，b，c，且（Ⅰ）证明：sinAsinB=sinC；（Ⅱ）若，求tanB.

探究：（Ⅰ）条件等式里面，边角共存，而结论却是单纯的关于角度的方程，所以根据正弦定理（a=2RsinA，b=2RsinB，c=2RsinC），将条件方程转化为角度关系，获得结论应该是必然的、自然的.

，即sinAsinB=sinAcosB+cosAsinB=sin（A+B）.

又sin（A+B）=sin（π-C）=sinC，所以sinAsinB=sinC.

（Ⅱ）由已知，，根据余弦定理有：

，所以

当前情况下，要求角B，角A已经确定，所以只要把（Ⅰ）的结论看成角B的方程，从中“种下”B消去C即可：sinAsinB=sinAcosB+cosAsinB，

所以，即sinB=4cosB，故tanB=4.

说明：在发展的过程中，“种下”目标元素，消去其他元素，问题就成功了一多半，剩下的就是“瓮中捉鳖”——如何解方程了.

例24 若△ABC的三个内角A，B，C成等比数列，它们的对边分别为a，b，c.（1）求B的取值范围，（2）若c2-a2=bc，求三个内角A，B，C的度数.

探究：（1）由A，B，C成等比数列，得B2=AC，要求B的取值范围，应该消去A，C得到关于B的不等式，，即B

因为0＜B＜π，所以B的取值范围是

另外，假设题给等比数列的公比为q，则：

所以

说明：三角形的三个内角成等差数列司空见惯，但是该题变成了等比数列，因此要注意审题.

求角B的取值范围，应该得到关于它的不等式、利用均值不等式，然后消去A，C，或者利用等比数列连续三项的常规设置，都能使问题迎刃而解.

（2）由c2-a2=bc最应该联想到余弦定理：c2=a2+b2-2abcosC.

后式代入前式整理可得b-2acosC=c.

利用正弦定理可将上式化为sinB-2sinAcosC=sinC.

又sinB=sin（A+C）=sinAcosC+cosAsinC，

后式代入前式可得-sinAcosC+cosAsinC=sinC，

也就是sin（C-A）=sinC，

所以C-A=C（不可能）或C-A=π-C即A=2C-π，

所以B=π-A-C=2π-3C.（三个内角都用一个未知量表示，这就是消元，肯定会便于后续的化简推算）.

又A，B，C成等比数列，所以B2=AC，

所以（2π-3C）2=（2C-π）C.

容易解得C=π（舍去）或，此时

说明：本题的考点是三角函数与数列的小综合，问题新颖别致，考查了正余弦定理和数列的知识，也考查了三角变形能力，方程组思想和消元意识是其中的主线.

要求三角形的三个内角，就应该列出关于它们的方程组，除了内角和那个天然的方程之外，还有等比数列对应的方程.第三个就要从第二小题去寻找和发展了，三个内角用其中之一来统一表示.这种消元就是本题的中心思想.