高中数学思想方法,函数的特性与应用

函数思想指根据题目结论的需要，结合条件信息构造相应的函数，通过函数关系，利用函数知识或函数观点观察分析转化和解决问题的思想.

经常利用的函数性质是函数的单调性、奇偶性、周期性、最大值和最小值、函数图象的变换与应用等，要求我们熟练掌握的是一次函数、二次函数、幂函数、指数函数、对数函数、三角函数的具体特性.

函数的奇偶性使我们可以由函数在已知区间的性质，推断其在关于原点对称的区间上的性质，用一句成语来概括即“事半功倍”；函数的周期性使我们可以由函数在某一周期上的性质，推断其在其他周期甚至在整个定义域内的性质，用一句成语来概括即“一本万利”.

例1 （1）已知3x-3y＞2y-2x那么（ ）.

A.x＞y B.x＜y C.x+y＞0 D.x+y＜0

探究：把3x-3y＞2y-2x规范一下，让两个字母变量分别位于不等式的两侧：3x+2x＞3y+2y，不等式两边结构相同，它们分别是某一个函数的两个函数值.

令f（x）=3x+2x，这显然是一个增函数，

原条件等价于f（x）＞f（y），

所以x＞y.

（2）判断20182019与20192018的大小顺序并说明理由.

探究：关于国际象棋发明者向国王申请奖励的故事大家都知道.指数的巨大威力，大家也略知一点，所以可以大胆猜测20182019＞20192018.

（当数字较大的时候，指数的作用可能远远大于底数）

要证明猜想，只能借助于对数，因为数值太大，对天文数字，对数可以简化一下；如果要结合函数，最好是自然对数.

要证明猜想，只要证明ln20182019＞ln20192018，即2019ln2018＞2018ln2019.规范一下，让两个数字分别位于不等式的两侧：

不等式两边结构相同，它们分别是某一个函数的两个函数值！

令，“导数的味道”，可用导数研究其单调性.

可得函数的减区间为（e，+∞），所以f（2018）＞f（2019），即（1）式成立，所以猜想正确.

说明：在比较数值的大小遇到困难时，作差法和构造函数法是两种常规选择.顺应题目特征，通过构造适当的函数，利用函数的单调性或图象是一种重要方法.

这种问题的关键是观察题目特征，主动去发现和应用函数的信息.要有函数意识，相关知识要熟练，要有敏锐的“嗅觉”，尽量让相同的字母或者数值集中起来，从中发现相同或相似的函数结构，函数思想就会自动地迸发出来.

应用函数思想的几种常见情境有：遇到变量，构造函数关系，建立相关元素的直接联系；有关的不等式、方程、最小值和最大值的相关问题，利用函数，可以直截了当地确立解题目标；含有多个变量的数学问题中，选定合适的主变量，从而揭示其中的函数关系；实际应用问题里，引进字母表示相关元素，将其转化成数学语言，建立数学模型和函数关系，应用函数性质进行研究，甚至数列的通项公式、前n项和公式，都可以看成项数n的函数.

例2 （1）已知等差数列{an}的前n项和为Sn，且S7=S16，a1＞0，判断Sn有最大值还是最小值、对应的n的值为多少.

（2）等差数列{an}中，是一个与n无关的常数，则该常数的可能值的集合为（ ）.

A.{1} B. C. D.

（3）已知两个等差数列{an}和{bn}的前n项和分别为An和Bn，且对任意正整数n都成立，则使得为整数的正整数n的个数是（ ）.

A.2 B.3 C.4 D.5

探究：（1）因为S7=S16，a1＞0，

所以根据等差数列的性质可知公差d＜0.

这是一个关于n的二次函数，其图象为开口向下的抛物线.

因为S7=S16，抛物线的对称轴为

所以n=11或12时，Sn取得最大值，无最小值.

（2）我们知道：等差数列的通项公式为n的一次函数，

an=a1+（n-1）d=dn+（a1-d），可以写成an=dn+b.

这样一来，，这是一个与n无关的常数，

所以分子分母中的一次项系数或常数项为零.

这里有两种可能：b=0或d=0，即或1.

（3）由（1）可设An=an2+bn，Bn=cn2+dn，

则对一切变量n都成立，

所以an+b=k（7n+45），cn+d=k（n+3）（k为常数），

所以An=kn（7n+45），Bn=kn（n+3）.

当n＞1时，an=An-An-1=k（14n+38）.

容易验证a1=A1=52k也符合上述通式，即an=k（14n+38）（n≥1）.

同理可得bn=k（2n+2）（n≥1），

所以为整数，

所以n=1，2，3，5，11，只有5种可能.

说明：上述三个小题都是等差数列问题，其通项公式和前n项和公式分别是项数n的一次和二次函数，而且后者没有常数项.当然，它们也可以利用数列的性质求解，但是利用函数思想，无论是理解问题还是解决问题，都比原来高了一个层次，方法也很简便.

用函数方法解决问题，正是函数思想的核心.

例3 （1）若a，b是正数，且满足ab=a+b+3，求ab的取值范围.

（2）若a，b是正数，且满足ab=a+b+3，求2a+b的取值范围.

探究：（1）方法一（函数思想）：

因为ab=a+b+3，所以

因为a，b都是正数，所以a＞1，

所以

令a-1=t（t＞0），即a=t+1，

则（当且仅当t=2即a=3取等号），

所以ab的取值范围是[9，+∞）.

方法二（方程不等式思想）：

因为a，b为正数，所以

又ab=a+b+3，所以

令，则t2-2t-3≥0，

所以t≥3或t≤-1（舍去），所以，即ab≥9.

（2）面对结论的不对称的结构，均值不等式好像不能直接使用了，我们只好回归到通性通法（函数思想）上来.

因为ab=a+b+3，所以

因为a，b都是正数，所以a＞1，

所以

令a-1=t（t＞0），即a=t+1，

则（当且仅当……）.

说明：求某些元素的取值范围问题，往往要根据题设条件构建关于它的目标函数，其中很可能由题给的方程（组）完成消元的任务.

当问题中出现两个量的积与和时，这就给出了使用均值不等式的明显信号，均值不等式选用得当的话，问题往往可以获得巧妙的解法.根据题给条件和结论的启示，可以在下列选项中选用其一：当然，我们还要注意等号成立的条件以及相关元素的正负号.

上述问题（1）的变式为若a，b是正数，且满足ab=a+b+3，求a+b的取值范围.你能找到三种不同的方法吗？答案是a+b≥6.

函数思想很多时候就表现为一种价值观念和自觉意识，遇到相关背景，应该自动地联想到函数思想方法.

利用函数思想研究相应问题，除了熟练掌握和应用函数的知识和方法，具备函数应用的自觉意识，还有以下三点值得注意.

（一）定义域优先，密切关注自变量的确切范围

定义域是函数三要素中最容易被忽视的，但它是函数研究的基础.定义域出错，可能前功尽弃，也可能一筹莫展.因为定义域有时候很可能给我们有益的启示，充分利用定义域的特殊性，可能把问题带入简化的方向.

例4 正三棱锥P-ABC的三条侧棱均为1，底面为等边三角形，求其表面积的取值范围.

例4图

探究：设∠APB=θ，则△PAB中，由余弦定理可得AB2=2-2cosθ，

所以三棱锥的表面积

因为

所以，所以

说明：本题考查三角函数的基本公式、余弦定理及其变形能力，但是利用函数思想解题，尤其要注意自变量的取值范围，这对空间想象能力提出了较高要求.这是本题的难点之一，我们可以从立体图形的两种极端状态来考察定义域：当三条侧棱夹角很小的时候，当顶点P无限靠近底面时.

例5 如图，公园里有一块边长为a的正三角形ABC空地，现修成草坪，D在AB上，E在AC上，线段DE把三角形分成等面积的两块，设AD=x.如果DE是灌溉水管，希望它最短，DE应该在何处？如果DE是参观线路，希望它最长，DE的位置又应该在哪里？

探究：要研究DE的长度的最值，当然是函数思想.题目已经给定了自变量：AD=x，所以我们可以大胆地去发展条件：

DE等分三角形的面积.

由题意得：2S△ADE=S△ABC，

即

例5图

由上式可得（一切都统一成自变量x的形式）.

设DE=y，在三角形ADE中由余弦定理可得：

自变量x的范围怎么样呢？直观简单地看，好像应该是0≤x≤a.但是，如果结合DE等分三角形面积这个条件，你会发现DE是一块“跷跷板”，当点D在最底部B的时候，E应该在AC的中点处；反之，当E下行至底部C处时，D恰好在AB的中点处，

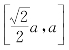所以f（x）在上单调递减，在上单调递增.

当时f（x）最小为，DE最短为

当时，当x=a时

所以当或者x=a时f（x）最大为，DE最长为(www.xing528.com)

也就是说，当DE平行于底边BC时，它最短；当DE成为一条中线时，它最长.

说明：函数的定义域，不能简单地静态判定，而应该用联系发展变化的观点去分析，要考虑各种要素之间的联系和变化.

这个问题在求最小值的时候，可使用均值不等式，但均值不等式无法确定最大值.这从一个侧面说明了函数思想的全面性和优势，它是真正的通性通法.

（二）恰当选择自变量

函数问题中，各种变量之间都有着千丝万缕的联系，它们之间的关系都直接或间接地体现着一定的规律.所有的变量中，目标变量一般来说就是因变量（函数值），我们应该选择那个与其他元素都有联系的元素作为自变量，而且这些联系最好是直接的，或者是容易求解的.

如果你认真分析，问题中总会有那个能与外界普遍联系的“一般等价物”，它就是我们需要的自变量.

自变量选择得当，不仅仅能快速简单的建立函数关系式，而且对后来的求解更有重要意义.

例6 某公司经营甲乙两种产品所得利润分别为P（万元）、Q（万元），利润P等于投资额，利润Q等于投资额的算术平方根的2倍，公司现有10万元资金可用于这两种产品的经营，问：如何分配投资才能获得最大利润？最大利润是多少？

探究：总利润y=P+Q，Q肯定是一个无理式，所以最应该让它简单一点，可以假设乙产品投资额为x（万元），则

甲产品投资额为10-x，P=10-x.

说明：选择自变量，首先让最复杂的部分得以简化，这就为后续函数的化简和研究带来了方便.其实这道题里，假设甲产品投资额为x，则总利润y，问题稍微复杂一点，但是依然可以求解，依然可以用换元法.你试试呗！

例7 圆锥的母线为1，其底面半径和高为多少时，其体积最大？

探究：如图，按照函数思想，应该构建体积的目标函数，那么，自变量选择圆锥的高还是其底面的半径呢？

将来计算体积，底面半径应该是平方运算，所以可设高为x，

则由勾股定理得底面半径

例7图

圆锥体积

导数是函数思想的重要工具，容易得到时，圆锥的最大体积为

说明：在上面的背景下，如果你假设底面半径为x，最后的体积函数将是一个比较复杂的无理式，求解难度会增大不少：圆锥体积（0＜x＜1），看起来比较复杂.你试试看，换元法可能使你豁然开朗.

在问题的研究过程中，我们要用发展的眼光去探测前进道路上的“暗礁”，防患于未然.本题里，也可以母线与高线的夹角为自变量，换元法可能起到大作用，你应该尝试一下.

例8 两县城A和B相距20km，现计划在两县城外以AB为直径的半圆弧上选择一点C，建造一座垃圾处理厂.调查表明：垃圾处理厂对城A城B的影响度分别与所选地点到城A城B的距离的平方成反比，比例系数分别为4，9；在上确定一点，使建在此处的垃圾处理厂对城A和城B的影响度之和最小.

探究：如图：

例8图

构建目标函数是必需的，要紧的是如何选择自变量和如何研究函数的最小值.这两个问题是相互关联的，自变量选择得当，函数性质的研究可能会降低不少难度.

方法1：设垃圾处理厂为C，∠CAB=θ，

则Rt△ABC中，AB=20，AC=20cosθ，BC=20sinθ.

根据题意，垃圾处理厂对两座县城的影响度之和：

（θ为锐角）.

如何研究该函数的最小值？

观察这个函数的结构特征，能看到cos2θ+sin2θ=1，你会闻出“均值不等式的味道”.

方法2：设垃圾处理厂为C，CA=x.

根据题意，垃圾处理厂对两座县城的影响度之和：

可以利用导数来研究函数的最小值，但是展望一下求导过程，很难不让人知难而退.果真如此吗？让我们试试看.

由可得：

18x4≥8（400-x2）2，所以9x4≥4（400-x2）2，所以3x2≥2（400-x2），

所以，所以函数的增区间为，减区间为

所以时函数取得最小值，

也就是垃圾处理厂到县城A的距离为

说明：一般来说，我们会根据结论适当结合条件来选择自变量，其中的自变量可能是角度、长度、时间等等.同等情况下，角变量优先，因为这样一来，灵活多变的三角公式就有了用武之地，它们可能会给我们带来极大的便利.

方法2给我们的启示是很多困难可能是我们想象出来的，扎扎实实地去做，不断关注能使问题简化的细节并加以应用，往往能从“山重水复”通向“柳暗花明”.

方法2中，如果结合一下换元法，令x2=t，问题会简化很多.你试一下？亲自实践，才能体验到真正的快乐.

总之，自变量的选择，要体现条件的直接联系，也要体现结论的需要，要用发展的眼光去分析去选择，应该去预测一下函数表达式的化简求解过程，不断提高自己数学研究的洞察力和预见性.真正“防‘繁’于未然”.

（三）研究最值问题和取值范围问题时，首选函数

有很多数学问题是求目标元素的最大值最小值或者取值范围的，它们往往都可以用函数思想来研究.

例9 （1）在直角△ABC中，，H是边AB上的动点，AB=8，BC=10，求的最小值.

（2）对某工厂的20件产品逐一检验，设每件产品为不合格品的概率都为p（0＜p＜1），且各件产品是否合格相互独立，如果20件产品中恰检验出2件不合格，则称其为二级事故.p为何值的时候二级事故的概率最大？

探究：（1）本题有明显的坐标系背景，而且在坐标系中可以比较容易地构建结论和条件的联系.

以A为坐标原点，AB为x轴，AC为y轴，建立平面直角坐标系，则A（0，0），B（8，0），C（0，6），设点H（x，0），则x∈[0，8]，

所以=（8-x，0）（-x，6）=-x（8-x）=x2-8x，

所以当x=4时，的最小值为-16.

例9图

说明：向量问题坐标化，不仅仅会给我们一种通用的计算方法，而且会大大简化思维的过程.

（2）这其实是一个独立重复试验，二级事故的概率f（p）=C220p2（1-p）18（0＜p＜1）.

要研究其最大值，最好对该目标函数进行求导.

由此可得函数的减区间为，增区间为

所以时，二级事故的概率最大.

说明：函数思想使得我们的思维变得明确起来，而且目标函数表达式看似复杂，但是利用导数，问题还是被顺利地化解了.只要研究最值问题，往往是构建函数，当然包括导数的方法，尽管该题属于概率内容.

例10 当时，关于x的不等式cos2x-mcosx+2m-2＞0有解，求实数m的取值范围.

探究：“不等式有解”就是个“能成立”问题，应该转化成函数的最值问题.

原不等式可化为m（2-cosx）＞2-cos2x，

所以

令2-cosx=k，则cosx=2-k，1≤k≤2，2-cos2x=2-（2-k）2=-k2+4k-2，

所以在1≤k≤2内有解，

所以

令，则：

f'（k）=，可得

所以f（k）在上为增函数，在上为减函数，

所以k∈[1，2]时，f（k）最大值为

最小值为f（1）=1，f（2）=1中的更小者，

所以m的取值范围是m＞1.

说明：不等式能成立（有解）和恒成立问题，一般都能转化成函数的最大值或者最小值问题.其中，把常数和变量分离，将问题转化成没有参变数的“规则函数”，问题一般会更加简便.

另外，本题中，在研究最小值的时候，面对这个典型的均值不等式结构，我们却不能使用均值不等式直接求出最小值，只能借助于函数的单调性.这再一次证明了函数的全面性的优势.函数方法就是最普遍的工具，但是如果改变问题为“求使cos2x-mcosx+2m-2＞0在x∈内恒成立的实数m的取值范围”，问题可能就简单多了.“能成立”问题变成了“恒成立”问题，则最小值问题应该变成最大值问题了，估计均值不等式的直接方法也应该能用得上了.你试试看？答案为

上面“恒成立”与“能成立”两类问题中，如果题目的其他信息完全相同，你能看出：如果其中一个转化成了最大值问题，则另一个肯定要转化成最小值问题.这是必然的吗？

例11 已知半径为3cm的球内有一个内接四棱锥S-ABCD，四棱锥S-ABCD的侧棱长相等，底面是正方形，当四棱锥S-ABCD的体积最大时，求它的底面边长和高.

探究：要研究四棱锥的最大体积，一般都要构造它的目标函数，按照结论要求可选底面边长x为自变量.

如图，假设四棱锥的高为SM，则M为底面的中心，球心O应该在线段SM上，连接OA，MA，则OS=OA=3，

例11图

Rt△OMA中，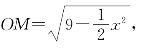

所以

四棱锥的体积

显然，这个表达式够烦人的.但是，从上述研究过程中我们可以发现，如果设四棱锥的高为x，则底面边长应该是一个二次根式，底面积便没有了根号，问题可能会大大简化.

假设四棱锥的高为SM=x，则OM=x-3.

Rt△OMA中，

所以

四棱锥的体积

这个函数表达式就简单多了，利用导数的方法，不难得到：当x=4时，体积取得最大值.

此时四棱锥的高和底面边长均为4.

说明：由此可见，自变量的选择还是有些讲究的.“多看几步棋”，选择得当的话，总可以“防‘繁’于未然”.

另外，在第一种选择中，，研究这个函数真的那么困难吗？可否用“换元法”试一下？

令，则x2=18-2t2，则

说明：这是一个三次函数，利用导数的方法，其实不像你想象的那么困难.做事要耐心细致，做题也是如此，坚持一下，可能马上会“雨过天晴”！