数学归纳法与其他数学方法结合，威力倍增

多种数学方法结合，不仅仅能降低问题的难度，也能让我们更轻松地发现问题的思路，快速地找到问题的解决办法.在n=k+1的证明当中，作差法、分析法大有用武之地.例8已经在一定程度上说明了这一点，所以数学归纳法考查的是综合能力.

作差法便于进行统一的推理和运算，而分析法的规范表述就体现出化简的原则：要证明一个复杂的结论，只要证明一个简单一点的结论，直到一个数学常识或者问题的条件.

例9 设正数数列{an}满足关系式an+1≤an-a2n，证明：对一切正整数n有

探究：（1）当n=1时，因为{an}是正数数列，所以a1-a21≥a2＞0，

所以0＜a1＜1，命题成立.

当n=2时，由于，所以命题成立.

（2）假设当n=k（k≥2）的时候，命题成立，即

则当n=k+1的时候，有（二次函数的最值问题）.

要证，只要证，k2-1＜k2，这显然成立，即当n=k+1的时候命题也成立，因此对一切正整数n都有

说明：在上面的论证中，对“ak+1≤ak-a2k”的研究，一是采用了配方法加以发展；二是在配方法之后，可以参考结论需要，合理地放缩到要证的结论.发展条件的时候注意到了结论的需要，首尾兼顾，问题也能解决，但是“n=k+1”的证明，最好使用分析法或作差法.这样一来，达成目标便会合理自然、水到渠成.

当n=k+1时，要证明，只要证明即可.

由此可见，作差法比原来的配凑法更自然、更流畅、更容易.

例10 对一切正整数n，判断并证明3n与n2+3n的大小关系.

探究：n=1时，3＜1+3，

n=2时，32=9＜4+6=10，

n=3时，33=27＞9+9=18.

结合两边的指数函数和二次函数图象可猜想：

n≥3时，3n＞n2+3n.

证明：假设当n=k（k≥3）的时候命题成立，即3k＞k2+3k，

则n=k+1时，要证明3k+1＞（k+1）2+3（k+1），作差法是一种常规方法.

3k+1-[（k+1）2+3（k+1）]=3×3k-[（k+1）2+3（k+1）]＞3（k2+3k）-[（k+1）2+3（k+1）]=2k2+4k-4＞0，即n=k+1时命题也成立.因此，对一切正整数n≥3，都有3n＞n2+3n.

说明：其实，我们都知道最后要证明的具体内容，利用作差法或分析法就能把要证结论的两边纳入同一个运算系统，进而采用统一的推理和运算.这种统一的系统会给我们带来极大的便利，而配凑法把两边割裂开来，人为因素太多、难度较大，不利于程序性地推理和运算.

例11 证明：（1）

(2)

探究：（1）n=2时，左边=，不等式成立.

假设n=k时不等式成立，即

则n=k+1时，

要证明

只要证明即可，

进而只要证明：，也就是即可，这显然成立，

所以n=k+1时，命题成立，

所以不等式对任意的n∈N，n≥2都成立.

（2）当n=1时，左边=1，右边=2，不等式成立.(www.xing528.com)

假设n=k时，不等式成立，即

那么当n=k+1时，

要证明，只要证明

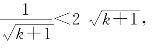
进而只要证明，即即可.接下来，问题便易如反掌了.

这就是说，当n=k+1时，不等式成立，

所以原不等式对任意正整数n都成立.

说明：在明确证明目标的前提下，分析法显然降低了问题的难度，使我们有章可循、有法可依了.

这里要注意：当n=k+1时，应该明确要证的目标；当代入归纳假设后，问题就被转化成另一个更简单的不等式了.认清当前目标后，运用分析法解答便是一个再正常不过的选择了.当然，利用配凑的方法解答也可以达到目标，但显然不及上述方法自然流畅.

例12 已知数列{bn}是等差数列，b1=1，b1+b2+…+b10=145.

（1）求数列{bn}的通项bn；

（2）设数列{an}的通项（其中a＞0，且a≠1），Sn是数列{an}的前n项和.试比较Sn与的大小，并证明你的结论.

探究：（1）设数列{bn}的公差为d，由题意得：

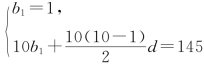，解得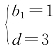，所以bn=3n-2.

（2）由bn=3n-2知，

而

因此，要比较Sn与的大小，可先比较与的大小.

取n=1，有

取n=2，有

由此推测

下面用数学归纳法证明①式.

（ⅰ）当n=1时，已验证①式成立.

（ⅱ）假设当n=k（k≥1）时，①式成立，

即

那么，当n=k+1时，

要证明

只要证明

也就是证明即可，而这等价于（3k+2）3＞（3k+1）2（3k+4）.

展开整理得9k+4＞0，这显然成立.这就是说，①式当n=k+1时也成立.

由（ⅰ）（ⅱ）知，①式对任何正整数n都成立.由此证得：

当a＞1时，，当0＜a＜1时，

说明：运用数学归纳法证明问题有两个优势：一是多了一个条件——归纳假设，二是我们很明确地知道结论是什么，而且两者之间有巨大的相同点和相似性，而作差法和分析法无疑会充分地利用这种优势.对二者规范的表述方式，将我们的证明带入既定的轨道，一切都会按照流程自动完成.

数学方法都是前人留给我们的宝贵的学科财富，它们在研究很多问题的时候都会给我们极大的便利，使得我们有章可循、有法可依.因此，对它们的学习和使用务必形成自觉意识.只有这样，才能使我们的研究顺理成章、如鱼得水.