高中数学思想方法：函数问题的放缩法

在函数与导数问题中，当指数、对数、三角函数和多项式结合到一起的时候，若要比较两个数或者两个函数值的大小，尤其是那些难度较大又无从下手的问题，常使用放缩法.其中，经常会用到x≥sinx（x≥0）、ex≥x+1、lnx≤x-1（x＞0）这几个重要结论.这三个不等式的证明用的是常规方法：作差构建函数，通过函数性质（最大值、最小值）来完成不等式的证明.它们的几何意义你知道吗？当不等式取“=”时，一次函数图象都是另一个函数图象的切线！请你把这些图象画出来，相信你的相关记忆会更加深刻.

例13 求证：ex＞3x-x2.

探究：因为ex≥x+1，所以可以借助中间变量x+1，只需证明ex≥x+1≥3x-x2，这有点太容易了！第一个等号当且仅当x=0时取得，第二个等号当且仅当x=1时取得，所以原结论中没有等号.

说明：如果不用放缩法，也可以采用作差法，构造一个新函数，用导数问题的一般方法处理.但是这样一来，运算量太大，思维链较长，中间还要设计一个“虚拟未知数”，对“设而不求”的要求也太高.

例14 求证：x+2＞0时，ex＞ln（x+2）恒成立.

探究：因为ex≥x+1（当且仅当x=0时取等号），

又因为lnx≤x-1，所以ln（x+2）≤x+1（当且仅当x=-1时取等号），所以ex＞ln（x+2）恒成立.

说明：同上，如果不用放缩法，也可以采取作差法构造新函数来处理，但是运算量要加大，思维链也要变长.其中，中间还要设计一个“虚拟未知数”.对“设而不求”的要求较高，你可以放手一试，或许会有意外的收获！

例15 （山东省2012高考理科22题）已知函数（k为常数，e=2.71828……是自然对数的底数），曲线y=f（x）在点（1，f（1））处的切线与x轴平行.

（1）求k的值；

（2）求f（x）的单调区间；

（3）设g（x）=（x2+x）f'（x），其中f'（x）为f（x）的导函数，证明：对任意x＞0，g（x）＜1+e-2.

探究：（Ⅰ）由，可得

因为曲线y=f（x）在点（1，f（1））处的切线与x轴平行，

所以f'（1）=0，即，解得k=1.

（Ⅱ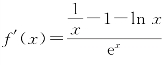），令f'（x）=0可得x=1，

而显然是个减函数.

当0＜x＜1时，，所以f'（x）＞0，f（x）单调递增；

当x＞1时，，所以f'（x）＜0，f（x）单调递减，

所以f（x）的增区间是（0，1），减区间（1，+∞）.

(Ⅲ)g(x)=(1-x-xlnx)，

显然，这个结论太熟悉了.得到这个结构，我们是故意为之）.

只须考察h（x）=1-x-xlnx＜1+e-2能否成立即可.

由h'（x）=-2-lnx＜0可得x＞e-2，

所以h（x）在x＞e-2时为减函数，在0＜x≤e-2时为增函数，

所以h（x）在x=e-2时取得最大值1+e-2，

所以

所以g（x）＜1+e-2（两次放缩过程中等号不可兼得）.

说明：对于最后一问，在函数表达式的化简过程中，一定要关注那些我们熟知的结构，让它们充分结合.这样，复杂的结论就可以转化为简单的函数问题.当然，总体上离不开放缩法的引导.

例16 已知函数f（x）=ex-1-x-ax2.

（1）当x≥0时，若不等式f（x）≥0恒成立，求实数a的取值范围；

（2）若x＞0，证明：（ex-1）ln（x-1）＞x2.

探究：（1）f'（x）=ex-1-2ax.

令h（x）=ex-1-2ax，则h'（x）=ex-2a（ex≥1）.(www.xing528.com)

①当2a≤1时，在[0，+∞）上，h'（x）≥0，h（x）递增，h（x）≥h（0）=0，

即f'（x）≥f'（0）=0，所以f（x）在[0，+∞）上是增函数.

此时f（x）≥f（0）=0，所以符合要求.

②当2a＞1时，令h'（x）=0，解得x=ln（2a）.

当x∈[0，ln（2a）]时，h'（x）＜0，h（x）单调递减，

所以x∈[0，ln（2a）]时，h（x）＜h（0）=0，即f'（x）＜f'（0）=0，

所以f（x）在[0，ln（2a）]上是减函数，所以f（x）＜f（0）=0，不合题意.

综上可得，实数a的取值范围是

（2）如果将结论用一般方法作差构建新函数，难度和运算量都太大，甚至无法进行.即使将结论变换一下，也无法继续.

两种超越函数凑在一起，会给我们制造很多麻烦！

很多综合题，当第二问遇到困难的时候，往往可以向第一问寻求援助！它们共同的结构是都有ex-1，而由第一问可知ex-1＞x+ax2，所以可以考虑放缩法：将ex-1缩小为一个二次函数.为了防止缩小过度，应该考虑a=时的结论，即x＞0时

欲证不等式（ex-1）ln（x+1）＞x2，只须证，也就是（超越函数与普通函数分离，函数之间的和与差总比函数之间的积或商更好研究）！

设

则.因为x＞0，所以F'（x）＞0恒成立，所以F（x）为增函数.又F（0）=0，所以F（x）＞0恒成立，所以结论成立.

说明：放缩法不可能一蹴而就.一般来说，难度较大的问题，会有一个不断试错纠错的过程.当然，有一些基本原则我们还是要坚持的.比如，要关注那些常见的结论；比如，放缩要尽量减少误差，只要能达到目的，误差越小越好；又如，尽量减少超越函数的种类；再如，把函数商积形式转化为和差的形式……

另外，从第一小题f（x）=ex-1-x-ax2≥0里面也可以分离出a≤，进而转化成新函数的最小值问题，难度不小，你可以试一下.

例17 已知函数

（1）若函数f（x）的最小值为0，求实数a的值；

（2）证明：ex+（lnx-1）sinx＞0.

探究：（1）

①当a≤0时，f'（x）＞0恒成立，所以f（x）在（0，+∞）上单调递增，无最小值.

②当a＞0时，f（x）在（0，a）上递减，在（a，+∞）上递增，所以fmin（x）=f（a）=lna=0，解得a=1.

综上所述，a=1.

（2）三个超越函数结合在一起，最好的办法是通过了放缩法把它们用多项式函数替换掉.当然，前一问的结论值得关注.

①当0＜x＜π时，x＞sinx＞0（这个结论容易证得），可得

由（1）得，，两边同时乘以sinx可得（lnx-1）sinx＞；又ex＞1，所以ex+（lnx-1）sinx＞0成立.

②当x≥π时，sinx≥-1，lnx-1＞0，所以（lnx-1）sinx≥-（lnx-1）=1-lnx.

欲证不等式ex+（lnx-1）sinx＞0，只须证ex-lnx+1＞0.

而此时ex＞x+1，x-1＞lnx，所以ex＞x＞lnx+1，所以ex-lnx+1＞0.

综上所述，ex+（lnx-1）sinx＞0恒成立.

说明：好像在导数不等式的证明题里面，只要结论中不带等号，是完全的不等号，它就散发着放缩法的“味道”.

在遇到和ex，lnx，sinx，cosx有关函数的时候，除了直接求导解决问题外，有的时候适当的放缩是无法被替代的.比如上述的几个例题，如果不放缩，解答起来将会非常麻烦.当然，对放缩的“度”需要认真把握.

放缩法在各种数学问题，尤其在具备一定挑战性问题的解答中有着广泛的应用.放缩也是一种化简.放缩之后，问题的结构应该更加简单、更加统一.如果能在放缩中实现消元的目的，无疑是一种进步.放缩不能随心所欲，要减少误差，要兼顾结论的需要.坚持以上原则，放缩法将会带给你意想不到的成功.实践证明，这一切都是必然的！