数列问题的解答,也经常“委托”放缩法,尤其在非常规数列的求和中,放缩法大有用武之地.
与数列求和有关的放缩法,“中间量”的选择要体现三个原则:一是熟面孔,二是便于求和与化简,三是“中间量”要介于不等式两侧之间.
先放缩再求和或先求和再放缩,哪项措施先行,取决于原表达式是否便于求和.一般来说,先求和再放缩,误差可能会小一点,也就是能求和的话尽量先求和,这也体现了化简优先的原则.但是,实际上很多时候,非常规数列不太便于求和,那就只能把它放缩成常规数列后再求和.
例6 函数![]() ,求证:
,求证:![]()
![]()
探究:由![]()
说明:此题不等式左边不易求和.此时,可根据不等式右边特征,先把分式分离变量,将分子变为常数(这样一来,不等式的左边会出现n个1,与另一边的n形成呼应),再将分式放缩成便于求和的形式(分母是单项式,与等比数列直接相关),继而求和即可.
若分子、分母同时存在变量时,要把分子配凑成分母的结构,拆分以后分子不再有变量.通常这种“分离变量”也是一种常见的化简方式.
例7 已知an=2n-1(n∈N*).求证:![]()
![]()
探究:因为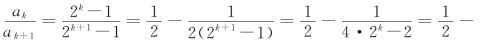
![]()
所以![]()
![]()
说明:上述过程中,我们逐项缩小.第一个化简举措是分离变量,消去分子中的字母n;第二个举措是把分母变成单项式,形成等比数列的态势,使之便于求和,从而达到证明目的,但是一定要注意到要逐项缩小,就是将减数的分母变小.
上面的两个例题中,我们都是坚持简化数列的原则:分母变成单项式,逐步靠近常见的等差、等比数列.如果能依据题目特征变成常数列,那将是更奇妙的结果.
例8 求证:![]()
探究:左边的项数为n2-n+1,要将其缩小为1,除了两端的两项之外,中间的分母都应该放大为单项式,所以左边>![]()
![]()
说明:这不是偶遇,坚持简化的基本原则,成功便会“顺理成章”.
放缩的过程中,要充分兼顾两边的需要:简化原数列,转化成单项式.这也体现另一边的需求——常数,分母尽量相同.
放缩的过程中,要尽量减少误差.要用最贴近的元素取代原来的元素.数列求和的时候,前几项最好直接计算,不要放缩.因为一般来说,放缩的过程中,前几项的误差最大.
裂项相消法是一种重要的数列求和方法,相关数列的基本特征往往是分子为常数,分母为某一等差数列的连续两项之积.
例9 (1)求证:![]()
(2)求证:![]()
探究:(1)![]()
所以![]()
![]()
(2)该题精确度要求高于第一小题,所以可以固定前几项不变,以减少误差.
说明:此题第二问采用了从第三项开始拆项放缩的技巧,比起第一问,误差大大降低了.放缩拆项时,不一定从第一项开始,须根据具体题型区别对待:放得太宽,超过限度,达不到证明目的;放得太窄,不能转化成常规数列,求和过程依然艰难.为此,要真正做到恰到好处:第一要兼顾到不等式两边的特征和需求,第二要积累相关的技巧和经验.
例10 设![]() 求证
求证![]()
![]()
探究:此数列的通项为![]()
因为![]() ,所以
,所以![]()
左边不等式的证明已经完成,如果借助于这种经验:
因为![]() ,所以Sn<2+3…+n+(n+1)
,所以Sn<2+3…+n+(n+1)![]()
但是![]() ,显然放得太大了.
,显然放得太大了.
可以用均值不等式进行放大,误差可能会小一点.
即![]() (https://www.xing528.com)
(https://www.xing528.com)
说明:1.应注意把握放缩的“度”:上述不等式右边放缩用的是均值不等式![]() ,误差较小;但是若利用数学常识
,误差较小;但是若利用数学常识![]() ,就放过“度”了!
,就放过“度”了!
2.一般来说,放缩法也应该体现化简的原则.使用均值不等式,一是可以完成放缩,二是能把“无理”数列变成了“有理”的数列.
3.放缩的“度”是可以把控的吗?
根据所证不等式的结构特征来选取所需要的放缩技巧(也包括重要不等式的使用)时,不等式另一边的信息非常重要,它很有可能就是某一个特定数列的前n项和.如果数列的前n项和是确定的,那么由此搞定它的通项公式,进一步确定放缩法的底线和目标也就易如反掌了.例10的结论中,中间是目标数列的前n项和,它的左、右两边肯定也是某两个数列的前n项和,其对应的通项公式便是我们放缩的目标.心中有目标,按图索骥总是容易得多.
因为看左边前n项和![]() ,所以通项公式bn=n,放缩方法:
,所以通项公式bn=n,放缩方法:![]()
所以右边前n项和![]() ,所以通项公式
,所以通项公式![]() ,放缩方法:
,放缩方法:![]()
例11 求证:![]()
探究:这是全国数学联赛的一道解答题,此题不易求和,所以应该将其放缩成便于求和的形式.
可否考虑我们的数学经验: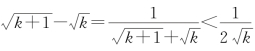 与
与![]()
![]()
该问题精确度要求较高,所以前几项应该尽量保持不变.
因为
所以![]()
![]()
因为![]()
所以![]()
![]()
说明:放缩法并不是神来之笔,它是可以把控的.只要坚持化简转化的基本原则,通过放缩法就可以把目标问题转化为常规问题.在转化的过程中,充分兼顾到不等式另一边的特征,再难的问题也能化解就在情理之中.
例12 数列{xn}中,![]()
(1)判断数列{xn}的各项与2的大小关系.
(2)求证:|x1-2|+|x2-2|+|x3-2|+……|xn-2|<2.
探究:(1)将递推公式“分离变量”,数列的发展规律就可能暴露出来.
![]() ,x1=1,则xn>0,
,x1=1,则xn>0,
且![]() ,所以xn≥1对一切正整数n都成立.(抽茧剥丝,数列的信息越来越丰富了)
,所以xn≥1对一切正整数n都成立.(抽茧剥丝,数列的信息越来越丰富了)
作差法是比较大小的通用方法.
因为![]() ,所以xn+1-2与xn-2符号相反,也就是相邻两项,一个大于2另一个必定小于2.
,所以xn+1-2与xn-2符号相反,也就是相邻两项,一个大于2另一个必定小于2.
而x1=1<2,则x2>2.
依此类推有x2n-1<2,x2n>2….
(2)根据结论特征可以猜测,这是一个无穷递缩数列的求和问题,我们可以转化成无穷递缩等比数列的求和问题.这期间,可能要用到放缩法.
因为xn≥1,所以![]() (只有n=1时,才能取到等号),
(只有n=1时,才能取到等号),
所以![]()
所以![]()
![]()
容易验证n=1时上式依然成立,所以原结论是正确的.
说明:放缩法与我们熟悉的知识和方法有机结合,会使我们的推理和计算如虎添翼.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




