高中数学：普通不等式的放缩法

由于证明不等式的需要，通过适当改变分式中分子或者分母的大小，或者多项式中增加或者减少一些项的方式，使不等式一边放大或缩小，让问题得以简化，或者让问题的结构更加整齐，朝着有益于结论的方向发展.

例1 若a，b，c，d∈R+，求证：

探究：记

观察上式的结构特征，考虑到原结论的需要，适当地将分子分母放大或者缩小，使得中间的分式容易进行求和计算，从而使表达式得以最终化简.

因为a，b，c，d∈R+，

所以（分母变大且统一），

（分母变小且统一），

所以1＜m＜2，即原式成立.

说明：=2（一个真分数的分子分母同时加上一个正数，分式值变大）也是一个不错的选择.

例2 设x＞0，y＞0，，求证：a＜b.

探究：_

说明：将左边“拆分”（通分的逆运算）比把右边通分更容易，而且给我们带来了新发现：左边的变化，终于和右边有了相同的成分和类似的结构.这样一来，找到放缩方式便水到渠成了.

例3 n＞2时，判断并证明log（n-1）n与logn（n+1）的大小关系.

探究：根据几个特例容易判断出：log（n-1）n＞logn（n+1）.

因为证明不等式最常用的方法是作差法，而且研究对数问题的时候一般遵循的是同底化原则.

所以k＞0，从而结论正确.

说明：放缩法与传统方法结合，证明过程极其优美.作差法是不等式证明的通常做法.同底化是研究对数问题的基本原则，对lg（n-1）lg（n+1）使用均值不等式，使之产生积极变化，从而完成本题的合理放缩，充分说明了一个辩证法则：变，就会有新发现.

解答下面这个问题，你是否感到容易多了呢？(www.xing528.com)

证明：当n＞2时，logn（n-1）logn（n+1）＜1，

你自己试试看，分析法与放缩法的结合会事半功倍！

当你对不等式的一边进行放缩的时候，不仅仅要考虑到有利于这边的化简和变化，还要考虑到目标结论的需求.这样，才能更好地克服盲目性，增强证明的自觉意识.

例4 已知a，b，c＞0，且a2+b2=c2，求证：an+bn＜cn（n≥3，n∈N*）.

探究：条件和结论都是齐次式，字母个数太多，考虑到这两个因素，可以将条件和结论分别变为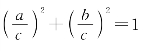和

说明：如果一个等式由齐次式构成，两边同时除以某一项，一般来说会收到化简的效果.也就是说，多个未知数的问题会变成只有一个新未知数的一元二次方程.如果两边同时除以交叉项，则会出现“均值不等式结构”，这也是齐次式的常规变化.

将条件和结论都如此转化，条件的化简结果就变成了结论放缩的中间量.

对以下问题，你是否胸有成竹了呢？先别看答案，放手一试呗！

★在△ABC中，a，b，c为三个内角A，B，C的对边，若a3+b3=c3，判断并证明该三角形是否是锐角三角形.

探究：由条件可以看出：三条边当中，c最大，所以角C是否是锐角便成了我们唯一的研究对象.

由余弦定理，只要证明a2+b2＞c2就可以确定该三角形为锐角三角形了.

所以该三角形为锐角三角形.

例5 三个不等正数a，b，c成等差数列，判断并证明an+cn与2bn的大小顺序（n是大于1的整数）.

探究：成等差数列的a，b，c三个字母一般可设a=b-d，c=b+d，三个字母减少为两个（d0）.

由二项式定理可得an+cn=（b-d）n+（b+d）n=2bn+2C2nbn-2d2+2C4nbn-4d4+…＞2bn.

看，此例中，消元法和放缩法结合得多么完美啊！

当然，这道题也可以运用数学归纳法证明.