作差法的常见应用及其探究

（一）作差法在比较代数式大小关系和证明不等式等方面大有作为

例6 （1）已知等差数列{an}的公差不为零，试比较a1a5与a2a4的大小关系.

（2）已知等比数列{an}的各项均为正数且公比不等于1，试比较a1+a5与a2+a4的大小关系.

探究：（1）设等差数列{an}的公差为d，则d≠0，则：

a1a5-a2a4=a1(a1+4d)-(a1+d)(a1+3d)=-3d2＜0，

所以a1a5＜a2a4.

（2）设等比数列{an}的公比为q，则q＞0，q≠1，

则（a1+a5）-（a2+a4）=a1（1+q4）-a1（q+q3）

=a1(1+q4-q-q3)=a1[(1-q)+q3(q-1)]

=a1(1-q)(1-q3)=a1(1-q)2(1+q+q2).

因为a1＞0，q＞0且q≠1，1+q+q2＞0，

所以a1+a5＞a2+a4.

说明：利用等差数列和等比数列的基本量（首项、公差、公比），能比较简单地表示目标元素.作差法将它们糅合成一个整体，剩下的就是代数式的变形和化简了.

例7 已知a＞0，a≠1，m＞n＞0，比较与的大小.

探究：

由题意，a＞0，a≠1.

当0＜a＜1时，

因为m＞n＞0，所以0＜am＜an＜1，0＜am+n＜1

所以

所以

当a＞1时，

因为m＞n＞0，所以am＞an＞1，am+n＞1.

所以

所以

综上可知，

说明：作差法判断大小的基本步骤是作差、变形、判号、结论，其中最关键的是“变形”.我们常把差式变形为积或商等易于判号的形式，以便于问题的向前推进.

另外，必要的分类讨论也为该题的不确定性清除了障碍.

例8 求证：x2cos2θ+y2sin2θ≥（xcos2θ+ysin2θ）2.

探究：左-右=（x2cos2θ+y2sin2θ）-（xcos2θ+ysin2θ）2

=x2cos2θ(1-cos2θ)+y2sin2θ(1-sin2θ)-2xysin2θcos2θ

=sin2θcos2θ(x2+y2-2xy)

=sin2θcos2θ(x-y)2≥0，

所以左≥右，原不等式成立.

说明：作差法之所以能给我们带来方便，是因为作差后容易进行化简，其中合并同类项、提取公因式、配方等过程都有利于我们最后解决问题.

（二）作差法可以研究两个函数间的关系

研究两个函数的交点情况，或者是研究两个函数值的大小关系，都可以运用作差法.因为这样一来，两个函数就变成了一个函数了，推理计算量就会减少很多.

例9 ，试判断x，sinx，tanx的大小顺序.

探究：方法1（作差法）：

设

因为f'（x）=1-cosx≥0在上恒成立，所以f（x）在单调递增，

所以f（x）＞f（0）=0，所以x＞sinx.

设

因为在恒成立，

所以g（x）在在单调递减，

所以g（x）＜g（0）=0，所以x＜tanx.

综上，当时，sinx＜x＜tanx.

方法2（数形结合构造法）：构造单位圆，如图，O（0，0），T（1，0），角x的终边与单位圆交于A.

做AM⊥x轴于M，NT⊥x轴交OA延长线于N.

由三角函数线可知：

例9图

因为S△OAT＜S扇形OAT＜S△ONT，所以sinx＜x＜tanx.

综上，当时，sinx＜x＜tanx.

说明：方法2太巧妙，巧妙得让我们都想不到！相比而言，方法1是通性通法，容易想，容易做.

例10 设函数f（x）=ln（1+x），g（x）=xf'（x），x≥0.其中，f'（x）是f（x）的导函数.若f（x）≥ag（x）恒成立，求实数a的取值范围.

探究：由题设得

已知f（x）≥ag（x）恒成立，即恒成立.

此时，问题如何进一步发展？

一般情况下，应该对上面的不等式进行“常变分离”.

恒成立（x=0时不等式显然成立，以下忽略x=0的情况）.问题便可由恒成立问题转化成函数（x＞0）的最小值问题.但是，当你真正研究这个函数的时候，会出现一定的困难.你试试看.

所以k（x）在（0，+∞）上为增函数.

又x＞0，所以k（x）＞k（0）=0，即x-ln（x+1）＞0恒成立，

所以h'（x）＞0恒成立，即h（x）在（0，+∞）上为增函数.

因为x＞0，所以我们要考察函数在无限接近于0时的函数值的极限，只能借助于洛必达法则：

所以a≤1

上述方法需要一定的补充知识和二次求导的复杂运算.真正研究此题的时候，我们可以改变策略.对于的发展，选择作差法是明智之举.

当a≤1时，φ'（x）≥0（当且仅当x=0，a=1时等号成立），

所以φ（x）在[0，+∞）上单调递增.其最小值为φ（0）=0，

所以φ（x）≥0在[0，+∞）上恒成立，

所以a≤1时，恒成立（当且仅当x=0时等号成立）.

当a＞1时，对x∈[0，a-1]有φ'（x）≤0，

所以φ（x）在[0，a-1]上单调递减，

所以φ（a-1）＜φ（0）=0（这一点如果结合函数此时的图象会更加明显），

即a＞1时，存在x=a-1＞0，使φ（x）＜0，

故知不恒成立.

综上可知，a的取值范围是（-∞，1].

说明：作差法的介入，使得问题的运算量大大地降低了.当然，分类讨论也对运算量的降低起到了一定的作用.当我们有两种选择的时候，作差法可能帮你省去一个大麻烦.

（三）作差法可以证明恒等式和条件等式

恒等式的证明，可以是发展化简等式的一边，推导出等式的另一边，或者是依次发展化简等式的两边.但是不管如何，当你发展一边的时候，既要关注已有成果，又要体现另一边的需要，也就是要同时兼顾到问题的两个方面.这样一来，就加大了我们探究思考的难度.

作差法证明恒等式和条件等式的时候，我们只需关注作差以后的唯一结果即可.再加上作差后的抵消、约分、并项、重组和有序排列等天然的化简效果，其难度和运算量肯定会大大降低.

例11 （1）求证：

（2）△ABC中三个内角A，B，C的对应边分别为a，b，c，

求证：

探究：（1）

所以原式成立.(www.xing528.com)

（2）在△ABC中，由正弦定理得

所以原式成立.

说明：上述两个小题都不难，可用多种方法完成，但是用作差法思路固定、方法单一，我们只需专注于运算即可，和谐自然，一切都会水到渠成.

例12 若△ABC中三个内角A，B，C都不是直角，

求证：tanA+tanB+tanC=tanAtanBtanC.

探究：△ABC中，C=π-（A+B），消元应该是最自然的选择.

观察上面的结构特点，有好多地方可以提取公因式，尤其是那两个分式，

所以原式成立.

说明：作差法有效地整合了待证等式的左右两边，使二者形成合力.需要注意的是，作差以后一定要观察其结构特征，力求变形化简.只有这样，问题才能朝着我们预期的方向发展.本题的提取公因式就让当前的表达式得到迅速的简化.

本题还有一种构造型的方法，非常简洁，只是我们不太容易想到.

因为C=π-（A+B），所以tanC=-tan（A+B），所以tanC=，去分母可得tanAtanBtanC-tanC=tanA+tanB，移项即得结论.

（四）作差法在数列问题中的作用

作差法在研究数列递推公式中，尤其是递推公式中an与Sn并存的情况下有重要作用.因为一般来说，我们认定Sn比an复杂，对于an与Sn并存的递推公式，可以将其中的任意的n代换成n-1或n+1，通过条件恒等式再制造一个等式；将得到的等式与原等式作差，不仅仅会消掉Sn，得到an与an-1或an与an+1间的“正统的”递推关系，而且可能还会有另外的惊喜——等差、等比数列可能就在不远处等着你.

例13 设{an}是正数组成的数列，其前n项和为Sn，并且对于所有的正整数n，an与2的等差中项等于Sn与2的等比中项.求数列{an}的通项公式（写出推证过程）.

探究：由条件可得，所以8Sn=（2+an）2.……①

n=1时，8S1=8a1=（2+a1）2，整理得（a1-2）2=0，即a1=2.

n≥2时，将①中的n换成n-1可得8Sn-1=（2+an-1）2.……②

①②作差可得8an=a2n+4an+4-（a2n-1+4an-1+4），

移项整理得a2n-4an-a2n-1-4an-1=0，

分组分解因式得（an+an-1）（an-an-1）-4（an+an-1）=0，

进而，（an+an-1）（an-an-1-4）=0.

因为数列{an}是正数数列，an+an-1＞0，

所以an-an-1-4=0，

所以数列{an}是以2为首项，4为公差的等差数列，

an=2+4(n-1)=4n-2.

说明：作差以后并不是就万事大吉了，应该对其结果进行全面的分析和化简.合并同类项或者分解因式会使问题产生积极有效的变化，浮云散去之后，问题的本质便会显露无遗.

例14 设数列{an}的前n项和为Sn，满足2Sn=an+1-2n+1+1（n∈N*），且a1，a2+5，a3成等差数列.

（1）求a1的值；（2）求数列{an}的通项公式.

探究：（1）n=1时，由条件可得2a1=a2-3，所以a2=2a1+3.

n=2时，由条件可得2（a1+a2）=a3-7，所以a3=2a1+2a2+7=6a1+13.

由题意可得2（a2+5）=a1+a3，所以2（2a1+8）=7a1+13，所以a1=1.

（2）n≥2时，将n代换成n-1可得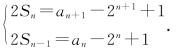

两式相减整理得2an=an+1-an-2n，

所以an+1=3an+2n，两边同时加上2n+1，可得：

an+1+2n+1=3an+2n+2n+1，

整理可得an+1+2n+1=3（an+2n）（n≥2），

又因为a1=1、a2=5满足a2+4=3（a1+2），

所以{an+2n}是等比数列，其首项为a1+2=3，公比为3，

所以an+2n=3n，所以an=3n-2n.

说明：作差以后，我们离等差或等比数列就不远了.对作差的结果进行必要的变换，使之向着等差或等比数列的方向转化，应该是我们处理这种问题的基本原则.

例15 已知数列{an}的前n项和为Sn，a1=1，an≠0，an·an+1=λSn-1，其中λ为常数.求该数列的前2m项之和.

探究：因为anan+1=λSn-1，……①

所以an+1an+2=λSn+1-1.……②

②-①可得an+1·（an+2-an）=λ（Sn+1-Sn），

即an+1·（an+2-an）=λan+1.

又因为an≠0，所以an+2-an=λ，

所以该数列的奇数项成等差数列，偶数项也是如此，公差均为λ.

直接使用条件anan+1=λSn-1，令n=1，可得a2=λ-1.

利用分组求和得

说明：好题不一定就是难题.本题考查的是对作差法的运用和分组求和的方法，难度不大，用到的知识和方法却不少.当然，在作差的过程中，因式分解等化简措施是十分必要的，它将问题间接地转化成了等差数列问题.

（五）解析几何中的作差法

平面解析几何问题的主要特征就是运算量大，审定运算目标、确定运算途径和过程、选择运算方法和工具往往是解析几何问题的中心内容.在这方面，作差法往往能独辟蹊径，前面的例4已经很好地说明了这一点.

例16 已知圆O：x2+y2=25和圆A：x2+y2-3x-4y-10=0，求两个圆的公共弦的长度.

探究：将圆O和圆A的方程作差可得直线l的方程3x+4y-15=0.

圆O：x2+y2=25和圆A：x2+y2-3x-4y-10=0显然有两个交点，两个交点都分别满足两个圆的方程，所以它们也满足直线l的方程，而经过两个交点的直线是唯一的，所以直线l就是两个圆公共弦所在直线.

在圆O中，由点到直线距离公式可得弦心距d=3，进而由勾股定理可得弦长为8.

说明：利用作差法直接得到公共弦所在的直线方程，这是解答本题的关键.

例17 （辽宁省高考题）已知椭圆上有一点F是椭圆C上的两个动点，如果直线AE与AF关于直线x=1对称，证明直线EF的斜率为定值，并求出这个定值.

探究：设E（x1，y1），F（x2，y2），又点在曲线C上.

由①②③两两作差整理得：

这个与条件中直线AE的斜率相关；

这个与条件中直线AF的斜率相关；

这个与结论中直线EF的斜率相关.

又因为直线AE与AF关于直线x=1对称，

所以kAE与kAF互为相反数，即④⑤左边之和与右边之和均为0：

将⑦⑧两式化为整式是一种化简：

两式作差的结果会更简洁：

3（x1+x2）+2（y1+y2）=0，所以

代入⑥得

说明：解决直线和曲线相交问题的关键在于用方程，对于这个“用”，人们的表现往往为直接解方程或者间接解方程.这个过程相对复杂且运算量大.而设交点坐标代入原方程作差，则是“巧用”方程，从而收到减少运算量化繁为简的神奇效果.上面的例题可充分地体现这一点.因此，在解答直线与圆锥曲线相交问题时，如果出现某条弦的斜率问题，作差法是一个简单而行之有效的选择.

本题也可以通过联立方程组求解，建议你再次体验设而不求的解题技巧，大胆地去做，问题可能没有你想象得那么难.

设直线AE方程：得：

设E（xE，yE），F（xF，yF）.

因为点与点E（xE，yE）为直线AE与椭圆的交点，其横坐标就是①的根，所以由韦达定理可得：

例17图

又直线AF的斜率与AE的斜率互为相反数，在上式中以-k代k，可得：

所以直线EF的斜率

即直线EF的斜率为定值

说明：第一种方法是作差法，只要认真观察其结构特征，就会发现或者开发出“点差法”与斜率的关系.它们不仅仅在形式上相似，而且在方法的本质上也一脉相承，可以通过运算的变换，直接得到结论.

第二种方法可以算作解答圆锥曲线问题的通法，联立方程组和韦达定理等往往都一气呵成.这种方法里面，因为两个交点中，已经知道了其中一个，所以另一个点的坐标可由韦达定理直接求出来.用上了这个特殊性，大大地简化了运算.另外，②的化简，是一个典型的大块代入，上述过程中有些省略，具体研究中一定要严格谨慎起来.

在方法2中，EF的斜率可以转化成三角形AEF的EF对应的中位线MN的斜率；其中，M为AE的中点，N为AF的中点.这样一来，研究M，N坐标的时候，中点坐标公式和韦达定理就会有一个完美的结合，运算量还会进一步降低，你不妨试一下.

本文通过案例，对高中数学中作差法的特点和用途进行了剖析和归纳.从中我们不难看到，作差法涉及的数学内容广泛，既具有我们传统理解中的比较大小的特性，又在数列、解析几何等知识中赋予了新的内涵.作差法的运用过程蕴含了函数思想、分类整合思想、化归与转化思想等，作差法在很多问题的解答中都有应用.