作差法：高中数学解题利器

作差法可以使问题产生结构性变化，在新的结构中会让我们发现并发展问题的隐含条件，推算出新的信息，激发我们的灵感，从而建立问题要素间的直接联系.

例1 O为△ABC内一点，，则O为△ABC的（ ）.

A.内心 B.外心 C.重心 D.垂心

探究：条件的发展，只能委托作差法.

因为，所以

所以，所以OB⊥CA.

同理，OA⊥BC，OC⊥AB，

所以O在△ABC三条高线上，必定是其垂心.

说明：作差法可以使问题出现新的结构和变化，我们的思路可能在这些新信息面前获得更加明确的方向.本题中，条件等式作差后，问题由数量关系转化成了位置关系，离结论更近了.

作差以后不能守株待兔，还要对作差结果进行积极的化简和分析，不断地推陈出新.

例2 数列{an}中，a1=1且an+1+an=6n-3，求数列{an}的通项公式.

探究：n=1时，a2+a1=3，因为a1=1，所以a2=2.

这不是一个标准的等差或等比数列，所以可以将递推公式“降格”后，两个等式作差可能会有所发现：n≥2时，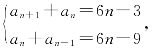

两式相减得an+1-an-1=6，

所以{an}的所有奇数项构成首项a1=1，公差为6的等差数列；

{an}的所有偶数项构成首项a2=2，公差为6的等差数列，

n为偶数时，an是所有偶数项中的第项，

n为奇数时，an是所有奇数项中的第项，(www.xing528.com)

综上所述，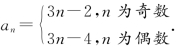

说明：正是因为作差出现的新变化，才使得问题出现了等差数列的特征，让问题的解决成为可能.

例3 已知数列{an}中，.问：数列{an}是否有最大项？若有请求出最大项；若没有，请说明理由.

探究：这是一个非常规问题，根据数列的通项公式很难求出其最大项.可以考虑根据导数进行研究，但是可能无功而返.你试一下？

令，由可得函数的单调减区间为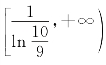、单调增区间为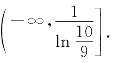

因为该题的自变量n是正整数，所以问题依然难办.

数列{an}若有最大项，设为第M项aM，最大项应该具备什么样的性质呢？

aM至少应该是个局部的最大值（“极大值”），即aM≥aM-1且aM≥aM+1.

我们看一下这样的“极大值”有多少，从中选拔出那个最大者.

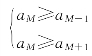等价于，解得9≤M≤10.

检验可得，这就是该数列的最大项.

这是待定系数法的思路.如果本题有多个极大值，这种方法也可以一网打尽.

我们还可以用另一种方法来考察数列这个特殊的函数：通过作差法来研究数列中相邻两项的大小关系，进而判断其“单调性”（后一项总大于前一项，则该数列当前递增；后一项总小于前一项，则该数列当前递减）.

显然，当n＜9时，an+1＞an，数列递增；当n＞9时，an+1＜an，数列递减.

当n=9时，，它们就是该数列的最大项.

说明：这个例题表明，作差法在研究比较大小的问题中优势非常明显.利用数列的特性和作差法得到的函数的单调性，数列的最大项便自动地“跳”了出来.

作差法应该是此类问题的首选，因为相邻两项的差，既不增加新的字母参数，又能看出数列的发展趋势.