高中数学思想方法：最值研究中广泛应用的换元法

例12 若4x-3·2x+1+8≤0，求y=（log2x）2-log2x2的最大值、最小值.

探究：令t=2x（t＞0），则原不等式可化为t2-6t+8≤0，

解得2≤t≤4，即2≤2x≤4，所以1≤x≤2.

令m=log2x（0≤m≤1），

则y=m2-2m=（m-1）2-1，

所以当m=1即x=2时，y有最小值，最小值为-1；

当m=0即x=1时，y有最大值，最大值为0.

例13 求函数y=cosxcos2x的最大值、最小值.

探究：y=cosx（2cos2x-1）=2cos3x-cosx.

令t=cosx∈[-1，1]，则y=2t3-t，

所以y'=6t2-1≥0，可得

所以函数y=2t3-t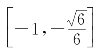在上递增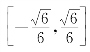，在上递减，在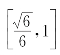上递增.

又t=-1时，y=-1，时，，

t=1时，y=1，时，，

所以函数y=cosxcos2x的最大值为1，最小值为-1.

说明：适当地选择“新元”，引进适当的代换，找到较容易的解题思路，就能使问题标准化.

例14 设F是抛物线C：y2=4x的焦点，斜率为-1的直线l交C于不同两点A，B，求的最大值.

探究：要求的最大值，首先要求它的函数关系式.

设直线l的方程为y=-x+b，将它代入y2=4x得x2-2（b+2）x+b2=0，

由题意得Δ=16（b+1）＞0得b＞-1.

设A（x1，y1），B（x2，y2），则x1+x2=2（b+2），x1x2=b2.

这是一个分式函数，并且分子是低次的、分母是高次的.这时常用的办法是令低次函数为t，然后可以将函数转化成我们更为熟知的函数.(www.xing528.com)

令t=b+3，则t＞2，

所以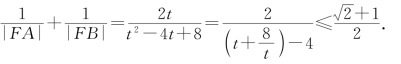

当，即时，取最大值

例15 在平面直角坐标系xOy中，已知椭圆的离心率为，左、右焦点分别是F1，F2，以F1为圆心、以3为半径的圆与以F2为圆心、以1为半径的圆相交，且交点在椭圆C上.

（1）求椭圆C的方程；

（2）设椭圆为椭圆C上任意一点，过点P的直线y=kx+m交椭圆E于A，B两点，求△ABO面积的最大值.

例15图

探究：（1）由题意知2a=4，则a=2.又，a2-c2=b2，可得b=1，所以椭圆C的方程为

（2）设A（x1，y1），B（x2，y2）.

将y=kx+m代入椭圆E的方程，可得（1+4k2）x2+8kmx+4m2-16=

据此容易得到

因为直线y=kx+m与y轴交点的坐标为M（0，m），所以△OAB的面积等于△OAM与△OBM的面积之和，即

把一切元素统一到根号之内，便于进行统一的观察分析，从而发现整体元素，进而可设，所以

将y=kx+m代入椭圆C的方程可得：

(1+4k2)x2+8kmx+4m2-4=0.

由Δ≥0可得m2≤1+4k2，所以0＜t≤1，

因此，故

当且仅当t=1，即m2=1+4k2时取得最大值

说明：最大值、最小值问题，最后往往都是在构造的目标函数中，观察那些带有规律的结构特征，发现那些高频率出现的整体元素，利用换元法，将其转化成二次函数或者均值不等式的结构.

尽管换元法可以帮助我们减少未知数的个数或者简化问题的结构特征、简化运算，但有些问题是不能用换元法解决的：研究函数的单调性奇偶性，讨论函数图象的对称性，这些问题都是对于原自变量而言的，换元法改变了自变量，形成了一个新函数，而新函数在上述方面的性质与原函数往往是不同的，所以此时再用换元法研究的就不是原来的内容了.

换元法有着极其重要的作用.换元法可以沟通数学各个分支之间的联系，可以扩大视野，培养我们的整体意识.对于一些较难的题目，我们还应当通过认真观察问题的结构特征，深入分析问题的隐含条件，采用类比、联想、猜测等手段进行适当的换元，并综合运用各方面的知识分析和解决问题.