数学方法：利用问题结构换元制造完美推理

均值换元法在这方面往往能大大地简化问题的运算.例如遇到x+y=S形式时，设，能够制造一些对称的结构；等差数列和等比数列的连续三项往往可以分别设x-d，x，x+d和，x，xq.实践证明，它们在后来的运算当中给我们省去了不少麻烦.

例3 （1）直角三角形ABC的三条边a，b，c成等差数列，求sinA+sinB+sinC的值.

（2）解方程：x4+（x-4）4=626.

（3）△ABC的三个内角A，B，C满足：B是A，C的等差中项，，求三角形三个内角的度数.（根据1996年全国理科数学试题改编）

探究：（1）不妨设c为斜边，则c2=a2+b2.

因为a，b，c成等差数列，所以可设a=b-d、c=b+d，故（b+d）2=b2+（b-d）2，整理可得b=4d，所以a=3d，c=5d，sinA+sinB+sinC=.

说明：若椭圆的长轴、短轴、焦距成等差数列，求其离心率；若双曲线的实轴、虚轴、焦距成等差数列，求其离心率.这两个问题，与刚才的问题有相同的结构，你能根据上面的推理马上给出答案吗？

（2）这是一道初中数学竞赛的题目，直接求解难度较大且很难入手，但是关注到原方程可转化为x4+（4-x）4=626，而x与4-x的平均数是常数2，原方程可转化为[2-（2-x）]4+[2+（2-x）]4=626.

我们可以考虑用平均值代换.设y=2-x，则原方程可化为（2-y）4+（2+y）4=626.(www.xing528.com)

配方可得[（2-y）2+（2+y）2]2-2（2-y）2（2+y）2=626.

整理得y4+24y2-297=0，所以（y2+33）（y2-9）=0，

所以y2=9，所以y=±3，即2-x=±3，所以x=5或x=-1.

（3）由已知容易得到

由A+C=120°进行均值换元.设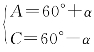（这是等差数列的常规设置，由此既可以简化条件等式——只有一个未知数的对称结构，更可以体现结论的化简需要：此时结论为cosα），代入已知等式得

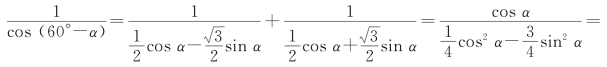
解得或（舍去），即α=±45°，所以三角形三个内角的度数分别为15°，60°，105°.

说明：利用两个元素的平均数进行换元，使得问题出现了对称的优美结构，很可能会在后来的运算中产生抵消、约分、合并等化简结果，给问题的探索和运算带来极大的便利.

对称是一种美，对美的追求，很有可能使问题变得简洁起来.