高中数学：基本量法与消元意识

金字塔

泰勒斯测金字塔高度

提及埃及这个神秘而又古老的国家，人们不约而同地会想到同样神秘的金字塔.泰勒斯游历埃及期间，看到人们都在看告示，告示上写着法老悬赏测量金字塔的高度.于是，他就去找法老……泰勒斯说只需要用一根木棍和一把尺子就能测量出金字塔的高度.他把木棍插在金字塔旁边，等木棍的影子和木棍一样长的时候，他量了金字塔影子的长度和金字塔底面边长的一半.把这两个长度加起来就是金字塔的高度了.在法老的请求下，他向大家讲解了如何从“影长等于身长”推测“塔影等于塔高”的原理.也就是今天所说的相似三角形定理.

泰勒斯（希腊语：Θαληζ，Thalês，英语：Thales，公元前约624年—约546年），希腊著名数学家和天文学家.数学上的泰勒斯定理和泰勒级数以他的名字命名.他是首次将一年的长度修定为365日的人.他亦曾准确地估量了太阳及月球的大小.

每个数学概念、定义、公式、定理都有对其起决定作用的量，即基本量.有很多数学题的解决都可归结到基本量上，找出基本量，从而应用这些基本量形成的系统来解决问题.在学习数学的过程中，我们会时常用到“木棍”和“尺子”这样的基本量.尽管人人都有这样的“基本量”，但也不是每个人都能测量金字塔的高度，所以在拥有基本量的同时还需要选择合适的方法.

数学题目中的元素可能有很多，若选择恰当的“基本量”并将所有元素都用基本量来表示，肯定会简化问题的运算，同时还便于发现和建立条件之间、条件和结论之间的联系，使得我们对数学问题的研究更有洞察力.

例1 一个正数，其整数部分是它的小数部分与其本身的等比中项（其整数部分的平方等于它的小数部分与其本身的乘积），求这个正数.

探究：这个正数的小数部分x和整数部分y就是该题的基本量.

该题富有挑战性，让我们去放手一搏.

由题意得y2=x（x+y），即x2+xy-y2=0（*），

所以（齐次式常用的处理办法），

解得（舍去负值）（此时就是黄金分割比），即

因为x是小数部分，所以0＜x＜1.

说明：整数问题常用的处理方法是列举法，所以当y=1时，x=，y=2，3，…时，x＞1不合题意，所以这个正数是（*）是齐次式，指每一项次数都相等的多项式；另外，（*）也可以看成关于x的一元二次方程（y看成任意实数）.你不妨用求根公式一试.

在解决问题的过程中，我们要有足够的耐心和信心.阳光总在风雨后.山穷水尽后的柳暗花明才是真正的成功，能坚持到最后的人才是胜利者.

对基本量的选择要坚持普遍联系和最简原则，也就是说，我们选择的基本量应该能够与题目中的其他元素建立起“体”“面”联系，基本量的个数要尽量少.

消元方法可以减少未知数或者变量的个数，起到化繁为简的作用.几乎可以肯定地说，“体”“面”的消元就是一种有效化简.一般来说，消元以后可能就更靠近结论了.

例2 设a≠b，解关于x的不等式a2x+b2（1-x）≥[ax+b（1-x）]2.

探究：该不等式中的元素个数有点多，问题有些杂乱，但是如果我们确定好问题的主要元素（基本量），问题就有可能简化.该题的主元是x，其他的不过是系数、常数而已.这样一来，解题目标便会明确下来.这是一个关于x的二次不等式，首先要将其标准化，合并同类项是主要手段.

将原不等式化为（a2-b2）x+b2≥（a-b）2x2+2（a-b）bx+b2，

移项整理得（a-b）2x2+（2ab-2b2-a2+b2）x≤0，

再整理可得（a-b）2（x2-x）≤0.

因为a≠b，即（a-b）2＞0，所以x2-x≤0，即x（x-1）≤0，

所以不等式的解集为{x|0≤x≤1}.

说明：确立主元意识，盯紧问题的基本量，就可以不断地对问题进行标准化整理，一旦变成标准问题，综合题就变成一个基本题了.

例3 一个等比数列和一个等差数列的各项都是正数，它们的首项相等，第三项也相等，判断它们的第五项的大小并说明理由.

探究：等差数列、等比数列问题的基本量，往往包括首项、公差、公比等多个元素，有点杂乱！

考虑到本题的实际情况，完全可以用它们的第一项a和第三项b来做本题的基本量.

等差数列中，第一项a、第三项b、第五项a5成等差数列，则2b=a+a5，所以a5=2b-a.

等比数列中，第一项a、第三项b、第五项b5成等比数列，则b2=ab5，所以

比较大小最常用的就是作差法，即

所以a5≤b5.

说明：解数列题常用的方法是基本量法.对此，如果能够适时地利用数列的性质，无疑能给问题的解决带来更多的机会和更多的方便.基本量法是指把条件和结论统一化归为首项和公差（或公比）的关系式，通过方程不等式（组）的变换，得到欲求的结果.这样做的缺点是有时候会产生较大的运算量，如果辅助以等差（比）数列的性质，可能更容易得到欲求的结果.一般来说，基本量是最基本的方法，只要有足够的耐心，一般涉及等差（等比）数列的问题都可以顺利解决.

例4 （1）已知等比数列{an}中，各项都是正数，且3a1、a3、5a2成等差数列，则=（ ）.

A.2 B.3 C.4 D.9

探究：设等比数列{an}的首项为a1，公比是q.

由3a1，a3，5a2成等差数列得2a3=3a1+5a2，即2a1q2=3a1+5a1q，

化简得2q2-5q-3=0，解得q=3或者（舍负值），

所以，选D.

（2）已知正数组成的等比数列{an}满足Sn=80，S2n=6560，且前n项中的最大项是54，求S10的值.

探究：设等比数列{an}的首项是a1，公比是q（a1＞0，q＞0）.

由题意得q≠1，

所以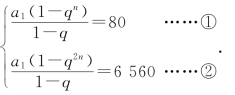

由得qn=81（作商消元是解决等比数列问题常用的方法），

所以q＞1，所以前n项中的最大项是，解得

将qn=81，代入（1）可得a1=2，q=3，

所以

（3）已知等差数列{an}，a1+a5=18，a2a4=65，则数列{an}的通项公式为_____________.

探究：数列{an}是等差数列，所以a1+a5=a2+a4=18，又a2a4=65（此时已经把四项的研究变成了两项），

解得或

所以数列{an}的通项公式为：

an=4n-3或an=21-4n.

（4）已知等比数列{an}中，且，a2a3=3，则数列{an}的通项公式为_________.

探究：数列{an}是等比数列，a2a3=a1a4=3，又（此时也是已经把四项的研究变成了两项），

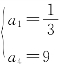解得或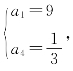

所以数列{an}的通项公式为：

an=3n-2或an=33-n.

说明：前两个题只用基本量法求解，而后两题辅以数列的性质进行转化，运算更加简洁.要综合考虑问题，单一的方法往往有一定的局限性.

形成好习惯，事半功倍.当消元成为一种习惯的时候，问题的基本量就自动形成了，很多问题的解决会水到渠成.请看下例.

例5 （1）的值为_________.

探究：观察三个角的关系25°=15°+10°，

所以

运用两角和的正、余弦公式展开整理即得：

上式=

（2）两个变量x，y满足x+y=1，求x3+y3的取值范围.

探究：由x+y=1得y=1-x，代入x3+y3中得：

说明：当然，如果你了解立方和公式a3+b3=（a+b）（a2-ab+b2），消元的过程会更简洁一些.

（3）二次函数f（x）满足f（1）=f（0）=1且f（x）≥x对一切x∈R都成立，试求f（x）的表达式.

探究：设二次函数f（x）=ax2+bx+c.

由f（1）=f（0）=1得，所以，

所以f（x）=ax2-ax+1（消元后，待定系数只剩下一个了）.

由f（x）≥x得ax2-（a+1）x+1≥0对一切x∈R都成立，

所以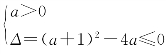，即，

所以只有a=1，f（x）=x2-x+1.

（本来是一个不等式问题，通过巧妙的消元，得到一个固定的答案）

说明：求二次函数表达式时，一般运用待定系数法.本题的待定形式还可以借助f（1）=f（0）=1直接设f（x）=ax（x-1）+1.

对上述问题的解答充分地说明，消元是一项十分重要的化简措施.当消元成了习惯，问题化简后条件结论之间的联系便一目了然了.

平面向量基本定理和空间向量基本定理实质上反映的就是基本量思想.基底就是表示该平面内的所有向量的“基本量”.向量问题的解决要善于寻找合适的基底，并将题目中所有的向量都用基底线性表示.

“平行四边形的四条边的平方和，等于两条对角线的平方和”这个问题的证明你还记得？（也是选用基本量进行发展的）空间向量的问题甚至也可以坚持这种方法.

例6 （1）在△ABC中，AB=3，AC=2，∠BAC=.

①求BC边上的中线AD的长.

②设P，Q是线段BC的三等分点，求的值.

例6图(www.xing528.com)

探究：设

①|a|=3，|b|=2，a·b=-3，

所以，所以

所以

②，所以

所以

说明：在探究中积累，在积累中总结，在总结中提高，在这个螺旋式上升的过程中，我们会越走越坚定、越走越远.

（2）若四面体ABCD有两组对棱互相垂直（如AB⊥CD，AC⊥BD），求证其第三组对棱也互相垂直（AD⊥BC）.

探究：这个问题也可以不必做辅助线，完全用向量的方法完成.

如图，我们先来构建基本向量，并由此发展条件.

设

因为AB⊥CD，所以=a·（c-b）=0，

所以a·b=a·c.

同理，由AC⊥BD可得a·b=b·c，

所以a·c=b·c.

发展条件到此结束，我们再去转化结论（AD⊥BC），

例6图

所以=c·（b-a）=b·c-a·c=0，

所以AD⊥BC.

说明：上述方法是综合法分析法的完美结合，其中的基本量（a，b，c）方法，不仅让条件得以发展结论得以转化，而且有效地沟通了它们之间的联系.

例7 已知实数a，b，c满足a+b+c=0，a2+b2+c2=1，求a的最大值.

探究：这道题在上一节已经顺利地利用配方法得以解决.换个角度会怎样？它山之石可以攻玉.本题中，元素个数太多，所以消元也应该是首选措施之一.

两个条件结合起来，尽最大努力消去b，c得到关于a的不等式，可能是解题的重要选项.

由c=-a-b，所以第二条件可化为：

a2+b2+（a+b）2=1，所以2b2+2ab+2a2-1=0.

将上述等式按照b为主元配方可得：

所以，所以

a的最大值为

代回（1）可得此时，进而

说明：请看，该题用消元法结合配方法使问题获得了更自然的解决.

其实，该题消元c以后的等式，可以看成关于b的一元二次方程.用判别式法构建关于a的不等式问题也不难解决，但是依然要验证等号成立的条件.你试一下？

例8 在△ABC中，角A，B，C的对边分别记为a，b，c（b≠1），且都是方程的根，求△ABC三个内角的度数.

探究：三角形问题中，三条边三个角就是基本量的全部，但是解题过程中，一般我们都是把这六个元素统一成三个内角或者三条边的形式，利用正弦定理或者余弦定理，达到消元减少基本量个数的目的.

解题过程中，一定要具备消元的自觉意识，见缝插针地消元，这肯定是一种进步.

由得

（同底化是解指数、对数问题的关键）

x2=4x-4，即x1=x2=2，所以

方法1：由C=2A得sinC=sin2A=2sinAcosA，

由正弦定理可得c=2acosA，

由余弦定理可得（角化边）.

又b=2a，代入上面可得

显然，a2+c2=b2，所以

方法2：由得b=2a.

由正弦定理sinB=2sinA，

因为B=π-A-C=π-3A（消元使得基本量变得单一有效），

所以上式可化为sin3A=2sinA即sin（A+2A）=2sinA，

展开得sin（A+2A）=sinAcos2A+cosAsin2A=2sinA，

所以sinAcos2A+2cos2AsinA=2sinA.

因为sinA＞0，所以cos2A+2cos2A=2，所以4cos2A=3，

因为C=2A，所以A为锐角，所以

所以

说明：两种方法，前者的基本量是边（甚至把三条边都转化成边a），后者的基本量是角.

例9 已知圆O的半径为1，P为圆外的动点，PA、PB为该圆的两条切线，A，B为两切点，求的最小值.

例9图

探究：该题的基本量应该是向量的夹角和模长，构建目标函数后，积极主动地去消元，应该是一种正确的方向.

设|PA|=|PB|=t，则=t2cos∠APB（∠APB应该转化成直角三角形中的∠APO）.

在Rt△APO中

所以，所以

令m=t2+1（m＞1），

所以（当且仅当时取等号）.

说明：解题过程中，将∠APB转化为∠APO是一个不起眼的进步，因为后者与直角三角形可以建立直接的联系.

实际上，选取|OP|=t作为本题的基本量更方便些.你试试吧.

例10 P，Q是椭圆上的两个点，O为原点，直线OP，OQ的斜率之积为，求证：|OP|2+|OQ|2为定值.

探究：解法1：设OP，OQ斜率分别为k，（这就是该题的基本量，可以用k表示与该题有关的所有因素：P，Q，|OP|，|OQ|，…）.

将OP方程y=kx代入得：

，所以，所以.

求|OQ|2的过程和结构与|OP|2的完全相同；若|OP|2=f（k），则，

所以|OP|2+|OQ|2=…=20.

说明：统一成一个量k后，一直往前走，别向两边看，就会融化在那蓝天里.按部就班的运算以后必定是问题的结论.

解法2：设P（x1，y1），Q（x2，y2），

则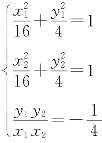，去分母就是一种化简.

结论是|OP|2+|OQ|2=x21+x22+y21+y22.怎样由条件①②③获得这种结论呢？字母太多——消元；形式不同，可将所有等式转化成同一种形式，即平方的总体结构.

考虑①②式的特征和结论的需要，可将③变形为x21x22=16y21y22.

由①②式得4y21=16-x21，4y22=16-x22，

分别代入上式得x21+x22=16.

又x21+x22=16-4y21+16-4y22，

所以y21+y22=4，所以|OP|2+|OQ|2=x21+x22+y21+y22=20.

说明：将③式平方是为了与①②式结合，同时适应结论x21+x22+y21+y22（都是平方关系）的要求，这个题也体现了代入消元的特征.

解法2里，出发点与突破口都是消元，其中的同构方法（函数思想）的应用也十分重要.

解法1利用了基本量，沟通了问题要素间的直接联系，显然比解法2更简单.

在解决数学问题的过程中，“基本量”法和消元法，都有着广泛而有效的应用，但需要我们有一双发现“基本量”的眼睛.基本量法结合消元法，就是把问题的所有信息，都统一起来集中地用基本量来表示，建立一种相对封闭的推理运算系统.在这个系统内，基本量沟通了所有问题要素的直接联系，不仅仅使得我们对问题的探究更有洞察力和预见性，而且很多时候还可以大大减少运算量.相信通过以上阐述，你会有意想不到的收获和感悟.