高中数学思想方法：韦达定理与配方法的应用

配方法运用得合理，会出现全新的结构特点.抓住这些特点，可以发现解题的捷径，避开那些不必要的计算或者简化很多烦琐的运算.

配方法是对数学式进行一种定向变形的技巧.通过配方后的新结构，可以更加清晰地观察到研究对象的性质和发展规律，取得化繁为简的效果，从而找到已知和未知之间的联系.

例1 已知△ABC的三个内角A，B，C，其中B为A，C的平均数，最大边，最小边是方程3x2-27x+32=0的两个根，求△ABC的面积和周长.

探究：2B=A+C，又A+B+C=180°，所以B=60°，最大边和最小边应该是另外两个角的对边a，c.

方程3x2-27x+32=0的两个根本来可以解出来，但是它们太“复杂”了，所以可以考虑运用韦达定理，“设而不求，瞒天过海”：a+c=9，ac=.

例1图①

如图，过A作AD⊥BC于D，直角三角形ABD中，斜边等于c，所以，三角形的面积.

例1图②

要求周长，只要搞定B的对边b即可.

请关注直角三角形.

由勾股定理可得：

所以该三角形的周长为：a+c+b=16.

注意：学了余弦定理，你肯定会找到更简洁的方法.

不过，这里还是要提醒一下：何时使用韦达定理呢？一般来说，在遇到字母系数的一元二次方程，或者尽管是数字系数但方程的解比较“复杂”的时候，应该考虑使用韦达定理.

“设而不求”就像孙子兵法里的“瞒天过海”，是一种比较高明的技巧，可以避开许多复杂的计算而直达解题目标.本题中，韦达定理和配方法为“设而不求”铺平了道路.

例2 （1）设a，b，c，x，y，z是正数，且a2+b2+c2=10……①，x2+y2+z2=40……②，ax+by+cz=20……③，则=（ ）.

A. B. C. D.

（2）已知长方体的表面积为11，其12条棱的长度之和为24，则这个长方体的一条对角线长为（ ）.

A. B. C.5 D.6

探究：（1）观察结论，我们可以猜测a，b，c与x，y，z可能有固定的倍数关系.在此基础上，我们尝试着对条件进行配方转化.面对三个条件等式右边的非零数字，可以在左边配方、右边为零这两方面进行兼顾.

①×4+②-③×4可得4a2+4b2+4c2+x2+y2+z2-4ax-4by-4cz=0，

即（2a-x）2+（2b-y）2+（2c-z）2=0，所以x=2a，y=2b，z=2c，

所以答案为C.(www.xing528.com)

（2）引进字母，将其转换成一个纯数学问题.

设长方体长、宽、高分别为x，y，z，则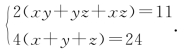

三个未知数两个方程.自由度告诉我们，一般来说，该方程组没有特定的解，而结论对角线长为.兼顾条件和结论的结构特征，可以发现条件的发展方法.

说明：对于上述两个例题，由于有意识地使用了配方法，解答过程既简单又优美.

配方法需要合理运用“裂项”与“添项”以及“配”与“凑”的技巧，从而完成配方.有时也将配方法称为“凑配法”.“凑配法”不能仅仅靠试探，综合考察条件和结论的特征并且将二者兼顾起来，可以有效地避免变换的盲目性.

配方法使用的最基本的依据是完全平方公式（a+b）2=a2+2ab+b2，灵活运用这个公式，可以得到各种基本配方形式，如：

结合其他数学知识和性质，还有另外的一些配方形式，如：

例3 已知x2-3x+1=0，求的值.

探究：该题结论复杂，所以可以从转化结论开始解答.

原式=

转化结论到此结束，下面据此发展条件，把条件等式两边同时除以x，可得，所以原式=8.

让难度再上一个台阶.除了使用刚才的配方法（从结论出发）之外，你完全可以从单一的发展条件一直通往结论.“发展”是一种数学研究原则，只不过发展条件的时候一定要结合结论的需要.

例4 x是方程x2-13x+1=0的根，则x4+x-4的个位数字为_________.

探究：发展条件：

转化结论：26887，所以个位数字是7.

例5 f（x）=ax，比较的大小.

探究：比较大小的通法是作差法.

把分数指数幂转化成我们更加熟悉的根式，可能更容易带来突破.

上式=.

说明：通分之后，你是否意识到：完全平方式可能就在你身边.这种比较大小的问题，最后往往能配成完全平方式.

你意识到该题的几何意义了吗？你画出指数函数图象，演示一下呗.