大样本平均数差异的显著性检验及其应用示例

Z检验是用正态分布的理论来推论差异发生的概率，从而比较两平均数的差异是否显著。它是通过计算两个平均数之间差的Z分数来与规定的理论Z值相比较，看是否大于规定的理论Z值，从而判定两平均数的差异是否显著的一种差异显著性检验方法。这种检验方法要求：（1）样本必须是随机抽取的；（2）变量必须是等距变量；（3）总体应呈正态分布。检验分为单总体检验和双总体检验两种。单总体检验是检验一个样本平均数与一个已知总体平均数的差异是否显著，也就是考察样本是否来自这个已知的总体。双总体检验是检验样本平均数所各自代表的总体的差异是否显著。

1.当总体服从正态分布，总体方差σ2σ已知时，要对样本平均数的总平均与总体平均数的差异性进行检验，Z检验公式为：

其中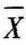是检验样本的平均数；u0是已知总体的平均数；σ是总体的方差，N是样本容量。

2.当N1、N2都是大样本容量时，两个样本相互独立，两个总体方差都已知时，要检验来自两个的两组样本平均数的差异性，从而判断它们各自代表的总体的差异是否显著。其Z值计算公式为：(www.xing528.com)

其中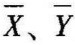，是样本1、样本2的平均数；σ1、σ2分别是两个总体的方差；N1、N2是样本1、样本2的容量。

比较计算所得Z值与理论Z值，推断发生的概率，依据Z值与差异显著性关系作出判断。

表11-4 双测Z检验统计决断规则