相关系数的计算方法与应用范围

相关是以量化的形式对客观世界中事物间普遍联系的反映。相关系数是用来描述两个变量之间变化方向和密切程度的数字特征量，一般用r表示，取值范围在﹣1.00和1.00之间。正相关是指两个变量的变化方向一致，当一个变量变动时，另一变量也发生相同方向的变化，如教师经济收入和职称高低之间的关系（在其他影响收入的因素基本相同情况下）；负相关是指两个变量的变化方向相反，当一个变量变动时，另一变量发生相反的方向变动，如某人的身体健康状况与发病率之间的关系；零相关是指两个变量之间的变化没有一定的规律，当一个变量变动时，另一变量不变或是呈现无规则变化，如某学生的成绩与他所住楼层的关系。从密切程度来看，无论两变量的变化方向如何，凡密切程度高的称为强相关或高度相关，密切程度一般的称为中度相关，密切程度弱的称为弱相关或低度相关。

应该注意的是，相关关系不等于因果关系。即使两个变量完全相关，也不能说两者之间存在因果关系。相关系数不是等距的度量值。例如我们不能说：相关系数0.5是0.25的2倍。此外，相关系数也不代表百分比，例如两变量的积差相关系数r＝0.30，不能说其间有30％的相关。

（一）积差相关系数

积差相关系数是由英国的统计学家皮尔逊（KarlPearson）提出的。它是测量两变量之间相关强度的“标准指标”。积差相关的使用条件是：（1）两列数据都是测量的数据，两列变量各自总体的分布都是正态的。（2）两变量为连续变量，即变量数值取自等距或等比量表。（3）两变量（x与y）分布具有直线关系，即一般而言，随x （或y）的增大或减小，y（或x）也呈相应的增长或减小的趋势。（4）必须是成对数据，每对数据之间相互独立。（5）N至少不能少于30，且两组数据的标准差近乎相等。它的基本公式如下：

其中，N为成对数值的个数，X为第一变量观测值，Y为第二变量观测值。

（二）等级相关

等级相关是由英国的心理学家和统计学家斯皮尔曼（Spearman）根据并延伸相关系数的概念而推导出的。等级相关是根据两列顺序变量数据中各对等级数据的差数来计算相关系数的方法。等级相关的使用条件是：（1）两列变量为等级变量。（2）两个相应的总体并不一定呈正态分布。（3）样本容量不一定大于30。可见，等级相关与积差相关相比，其优越性在于它不限制变量的分布形态及样本数量的大小，且运用范围更广，可用于顺序、等距与等比变量。缺点是等级相关的精确度一般差于积差相关。

等级相关系数的计算公式如下：

其中，D表示配对等级间的差数，∑D2表示配对等级间差数之平方和，N表示配对等级个数。(www.xing528.com)

（三）肯德尔和谐系数

肯德尔和谐系数又称肯德尔W系数，是表示多列等级相关程度的统计指标。比如说适用于多个评分者评定N个人或N件作品的等级；或者同一个人先后多次评定N个人或N件作品的等级时，计算其相关程度或信度。

计算公式为：

其中，K表示的是等级数量的列数或评价者数目，N表示的是被评价对象数目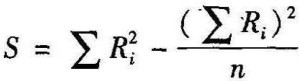，，Ri表示每一对象被评等级的总和。

（四）点二列相关

点二列相关是一种计算一列变量为量，另一列变量为质的相关统计方法。适用于两种变量中，一种为来自正态总体的等距或等比的测量数据，另一种为二分称名变量，即按内容的某一性质只能分为二类相互独立的变量。点二列相关在教育科研中常作为选择题的区分度指标。它的基本计算公式如下：

其中，p表示的是二分称名变量中某一值的变量比例；q表示的是二分称名变量中取另一值的变量比例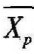；表示的是等距（比）变量中与p对应的那部分数据的平均值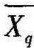；表示的是等距（比）变量中与q对应的那部分数据的平均值；Sx表示全部变量的标准差。