(1)学科交叉高频词统计及矩阵形成。
根据以上分析得到的学科之间交叉情况的数据,本章将以排名首位的两学科交叉D和F、三学科交叉D、F和G,以及四学科交叉C、D、F和G为例,分析学科交叉的热点。首先利用Bibexcel软件对从ERU采集的相关学科交叉数据进行关键词词频统计(见表6-2),然后挑选高频关键词,形成相关共词矩阵(见表6-3、表6-4、表6-5)。得到的关键词中存在一些无意义的关键词和与其他关键词联系较少的关键词,这些关键词不但对后续分析没有实质贡献,而且会影响分析结果,因此手动将其从高频关键词中剔除。对关键词作处理后,生成高频关键词共词矩阵。共词矩阵是一个N乘N的对称矩阵。共词矩阵中关键词的共现次数不仅计算在同一篇文献中共现的次数,而且还要计算同一Session ID中不同文献关键词的共现次数。对于同一篇文献中关键词的共现次数,赋值为1;同一Session ID出现的关键词的共现次数,赋值也为1。
表6-2 高频关键词分布表(降序)
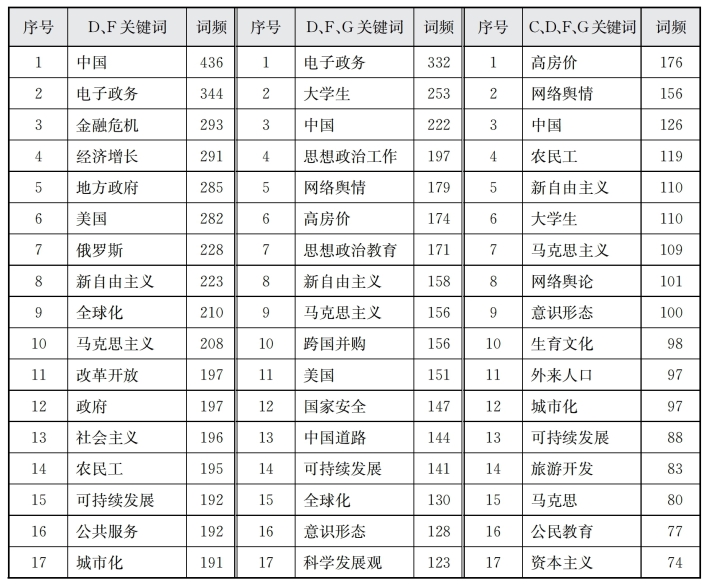
(续表)
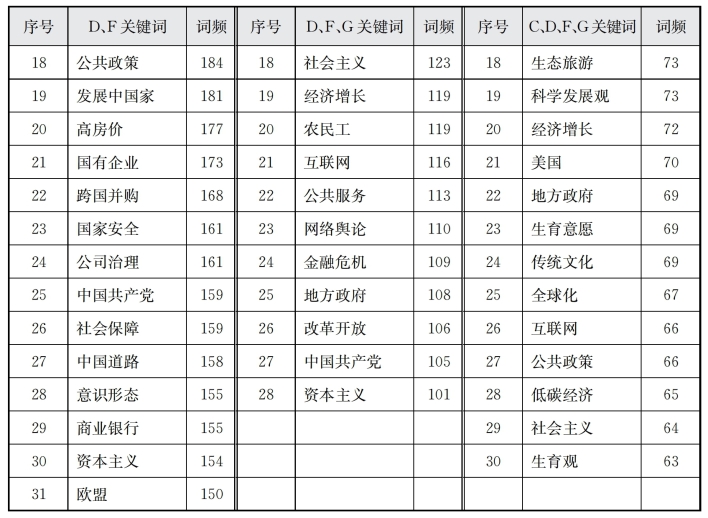
表6-3 D、F共词矩阵(部分)

表6-4 D、F、G共词矩阵(部分)
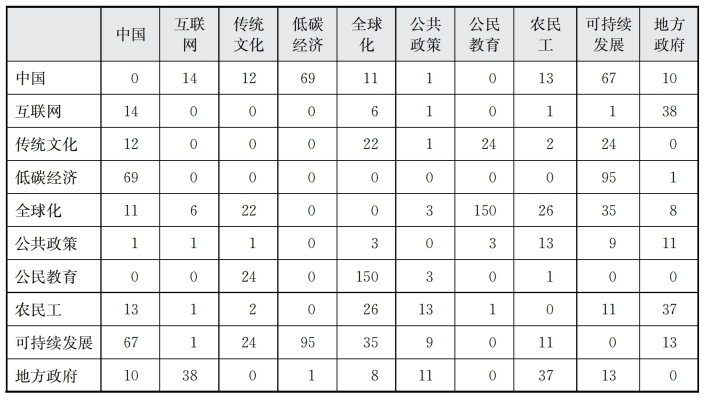
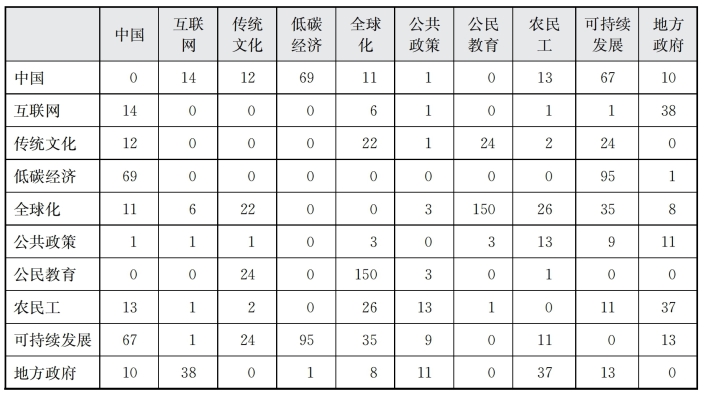
表6-5 C、D、F、G共词矩阵(部分)
(2)分析方法与步骤。
在学科交叉热点分析中,以SPSS软件作为统计分析的工具。首先,需要验证样本数据类型,通过验证,相关矩阵数据不符合正态分布和均匀分布。基于此,接下来采用与数据类型相适应的多元统计分析——因子分析和聚类分析。
在因子分析中,笔者考虑到所建矩阵包含有内在共词关系和外在共词关系的因素,而且邱均平已在其文章中验证可以将原始矩阵直接作为输入矩阵,事先不需要任何转化[15];另外,SPSS软件为了消除不同变量间量纲和数量级对结果的影响,在该过程中默认自动进行标准化处理,因此不需要对这些变量提前进行标准化处理,故本章研究的矩阵均未进行转化。在此基础上,利用主成分法、相关性矩阵与旋转——最大方差法进行因子分析。
因子分析的结果并不是最终的结果,降维是为了使我们的思路更加集中,但降维结束后得到的却未必是我们所期望的。为了更好地加以分析,我们可以在降维因子分析的基础上对得到的潜在因子进行聚类分析,加强分析结果的价值。
聚类分析中,共词矩阵也未作转化,运用系统聚类、相似性矩阵、组间连接和余弦方法进行聚类分析。
(3)结果分析。
①D、F学科交叉热点分析。
●因子分析结果
表6-6显示,提取因子后公因子方差的值均很高,表明提取的因子能很好地描述这31个关键词。表6-7因子分析方差分解表(解释的总方差)表明,前7个因子特征值大于1,这7个因子能够解释31个指标的81.229%,而仅前3个因子的信息解释量就达52.997%。图6-1的D、F因子分析碎石图也表明,从第8个因子开始,特征值差异减小。综合以上结果,提取前7个因子。
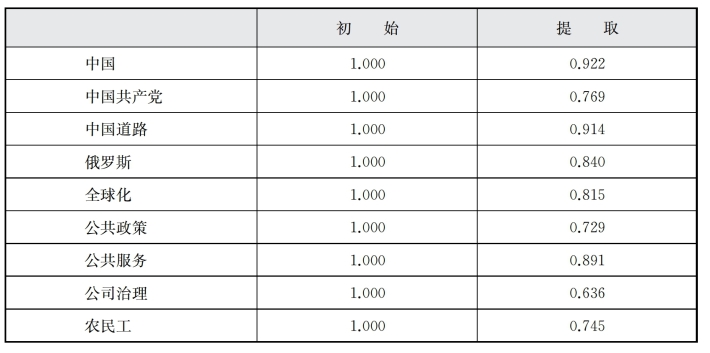
(续表)
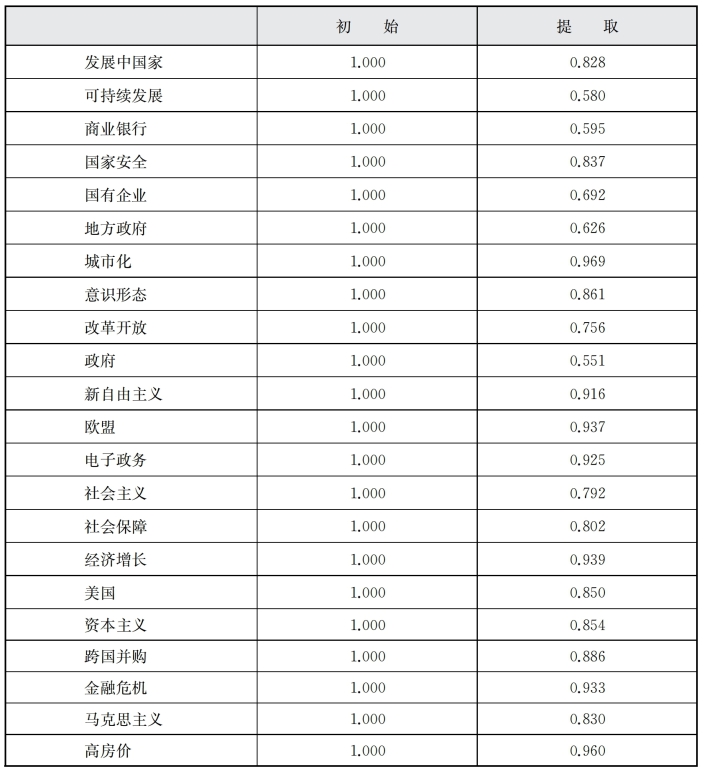
表6-7 D、F解释的总方差
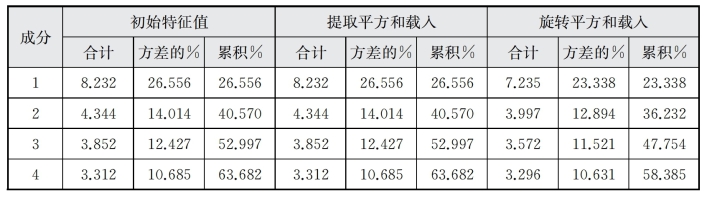
(续表)

图6-1 D、F因子分析碎石图
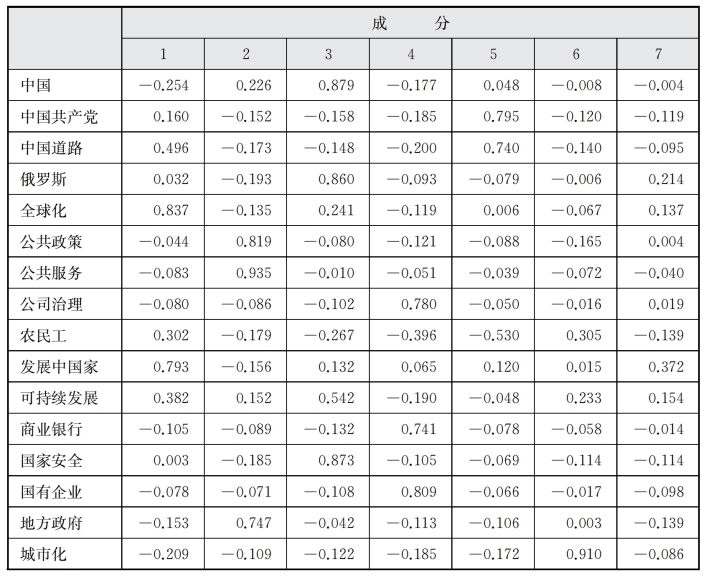
表6-8 D、F旋转成分矩阵
(续表)
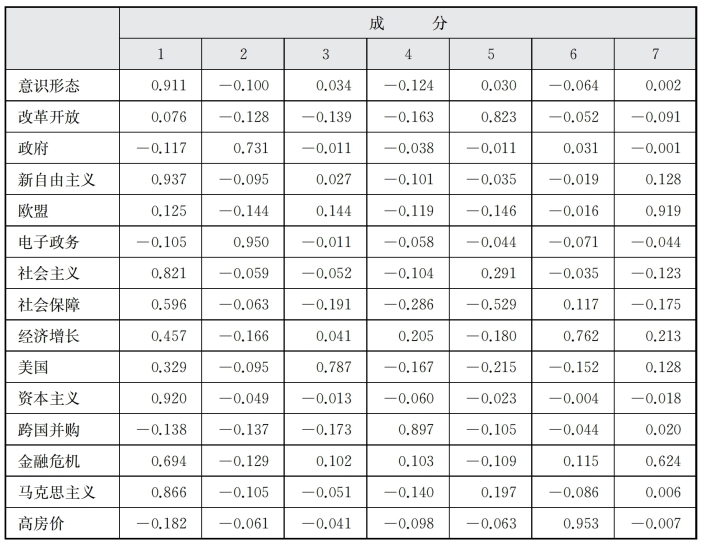
由表6-8因子分析旋转成分矩阵可以看出,经旋转后,因子便于命名和解释。为便于识别,将因子负载绝对值大于0.5的关键词制作成表6-9。
表6-9 因子分析确定的D、F学科交叉热点研究

(续表)
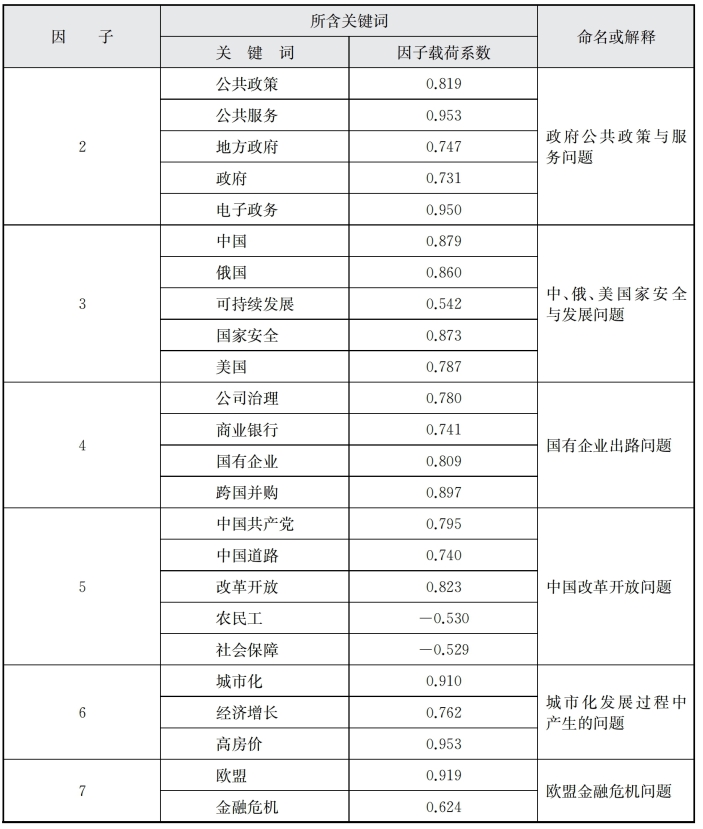
从表6-9因子分布情况可以看出,因子分析结果中的关键词总体分布有如下三个特点:
第一,绝大多数关键词都归至相应因子。根据因子载荷大于0.7就对因子解释有帮助的原则,并综合因子中其他关键词的属性,笔者对7个因子进行归类命名和解释,如表6-9所示。
第二,有2个关键词跨区分布。关键词“金融危机”同时出现在第1、第7个因子中,它们的因子载荷系数均在0.6左右,体现这两个因子——“新自由主义问题”“欧盟金融危机问题”之间的相关性。
第三,有2个关键词的因子载荷系数为负,同相应因子构成负相关关系——第5个因子中的“农民工”(因子载荷系数为-0.530)、“社会保障”(-0.529)。
●聚类分析结果
D、F关键词与序号对照见表6-10。(https://www.xing528.com)
表6-10 D、F关键词与序号对照表
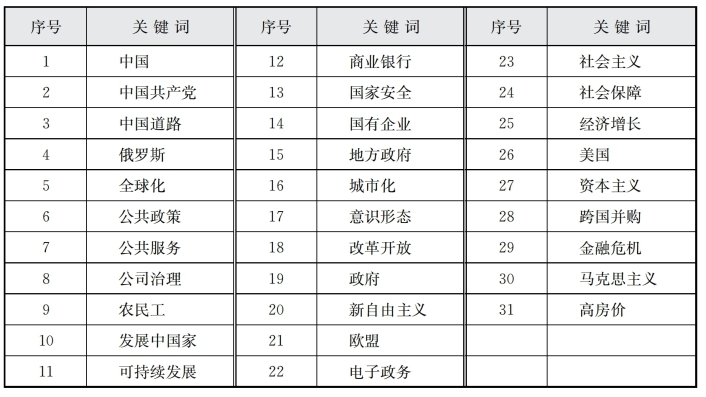
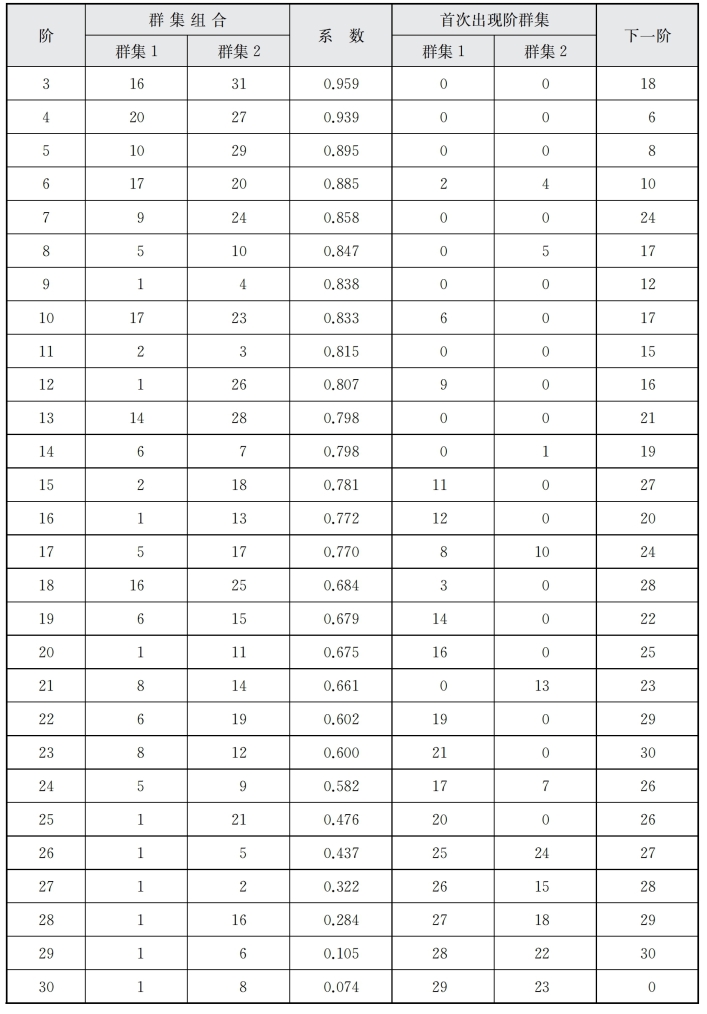
如表6-11所示,“阶”是指系统聚类分析的次序;“群集组合”的两列表示哪两个样本或小类在此步聚类;“系数”是指个体距离或小类距离;“首次出现阶集群”的两列是指此处参与聚类的是样本(0表示样本)或小类(非0表示小类);“下一阶”是指在后面哪步使用到此聚类结果。例如,在首步中,7号关键词(公共服务)与22号关键词(电子政务)聚类为一,系数(个体距离)是0.995,将在第14步中使用到本小类,同理依此可知余下聚类结果。
表6-11 D、F聚类表

(续表)
如图6-2所示,它以“树状图”的形式展示出与表6-11所示的凝聚状态表一致的系统聚类分析过程。例如,7号关键词(公共服务)与22号关键词(电子政务)距离最近,首先合并成一类,然后再与6号关键词(公共政策)合并,依此类推。
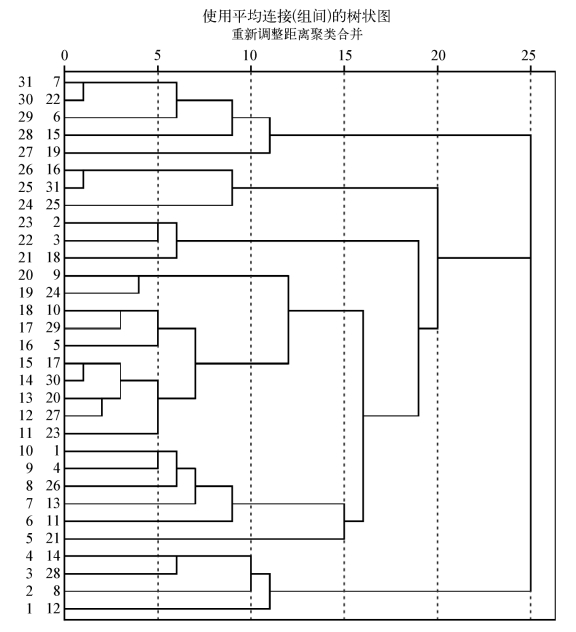
图6-2 系统聚类分析树状图
如果没有因子分析的结果作比较,仅依靠聚类分析的结果,分析难度明显较大,既无法确定分为几类合适,也无法取得对聚类的类进行命名的依据。以此结合因子分析的效果,可以明确地将关键词分为6大类:新自由主义问题、政府公共政策与服务问题、国家或区域的国家安全与发展问题、国有企业出路问题、中国改革开放问题、城市化发展过程中产生的问题。需要说明的是第9号关键词“农民工”在因子分析中与第5个因子是负相关关系,而又与其他因子没有正相关关系,但是与第24号关键词“社会保障”又是紧密相关的(都与第5个因子是负相关关系)。而第21号关键词“欧盟”所属同一个因子(第7)的第29号关键词“金融危机”是跨因子分类的,二者无法再聚类,则其与第3个因子的所有关键词聚为一类,形成国家或区域的国家安全与发展问题研究。归纳以上分析,最后确定D、F学科交叉热点分析结果如表6-12所示。
表6-12 D、F学科交叉研究热点

②D、F、G学科交叉热点分析。
此分析过程与D、F学科交叉热点分析过程相同,不再赘述。下面直接展示因子分析和聚类分析结果。
D、F、G关键词序号对照见表6-13。
表6-13 D、F、G关键词序号对照表

由表6-14可以看出,经过因子分析后,有7个因子被提取出,绝大多数关键词都归至相应因子。但是关键词“可持续发展”“跨国并购”“高房价”由于其因子载荷系数小于0.5而不能够参与分类。而第5个因子中的关键词“网络舆情”(-0.907)、“网络舆论”(-0.887)、“互联网”(-0.720)、“经济增长”(0.519)因为负相关因子较多,主题都与“网络”相关,反而成为主流。第7个因子中只有一个因子载荷系数绝对值大于0.5的关键词“农民工”(-0.783),成为一个相对独立的新主题。再结合图6-3聚类分析的结果,基本可以分为6类,见表6-15。
表6-14 D、F、G旋转成分矩阵
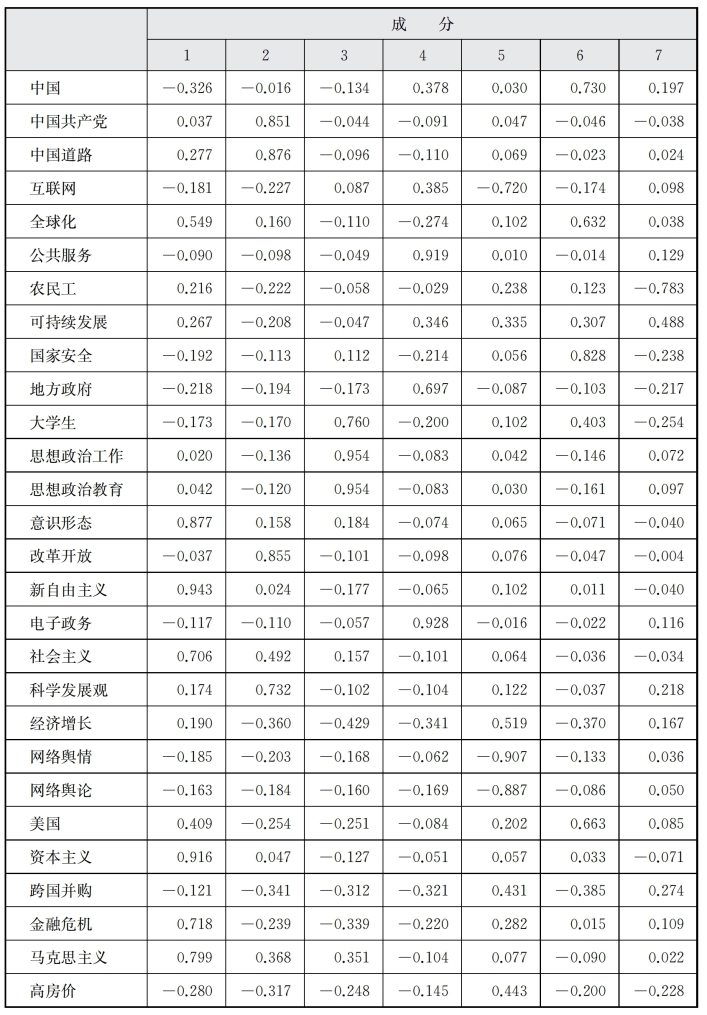

图6-3 D、F、G系统聚类分析树状图
表6-15 D、F、G学科交叉研究热点

(续表)

③C、D、F、G学科交叉热点分析。
运用相同的分析方法再对C、D、F、G学科交叉热点分析,展示因子分析和聚类分析结果。
表6-16 D、F、G关键词序号对照表
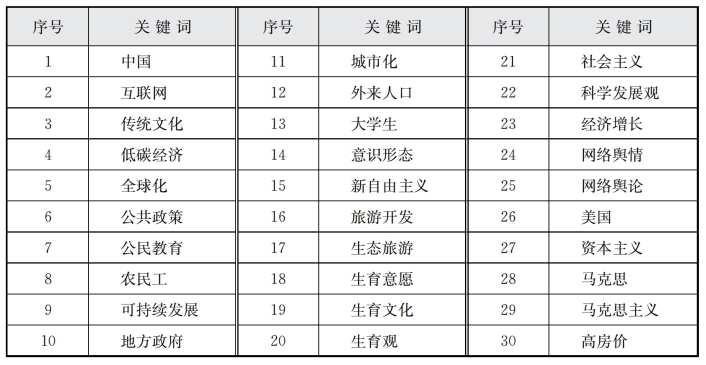
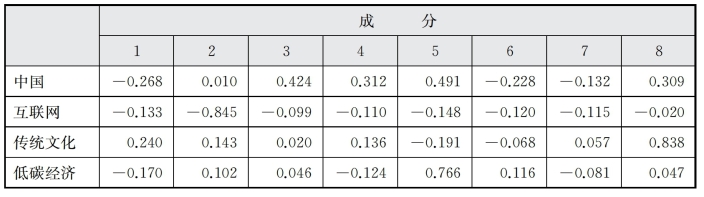
表6-17 C、D、F、G旋转成分矩阵
(续表)

D、F、G关键词序号对照见表6-16。
由表6-17可以看出,经过因子分析后,有8个因子被提取出,绝大多数关键词都归至相应因子。但是,关键词“中国”“大学生”由于其因子载荷系数小于0.5而没有参与分类。关键词“城市化”同时出现在第5、第6个因子中,它们的因子载荷系数在0.6左右,体现出“城市化问题”与“农民工问题”两个因子之间的相关性。第2个因子中的关键词“网络舆情”(-0.909)、“网络舆论”(-0.871)、“互联网”(-0.845)、“地方政府”(-0.634)均为负相关因子,仍可看作一类。第7个因子中关键词“科学发展观”(-0.523)与相应的因子之间的相关度较低。第8个因子“传统文化”成为一个相对独立的新主题。最后结合图6-4聚类分析的结果,可以分为8类,见表6-18。
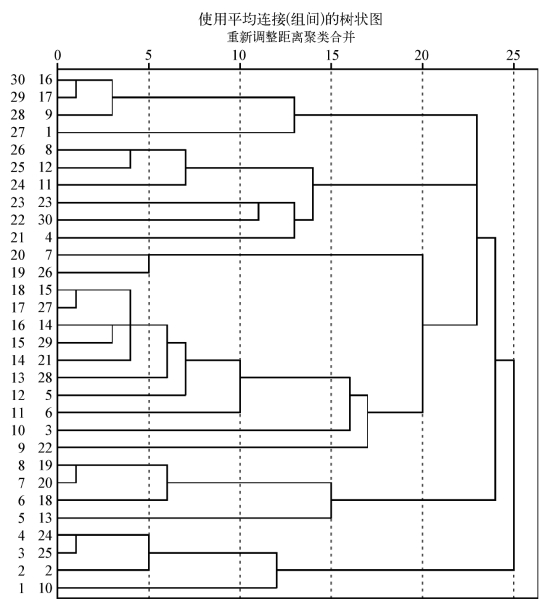
图6-4 C、D、F、G系统聚类分析树状图
表6-18 C、D、F、G学科交叉研究热点

(续表)

④学科交叉研究热点综合分析。
从表6-12、表6-15、表6-18对比分析可以看出,各个学科由于发展程度不同,研究重点不同,对于相同的问题的认识解决程度也不同。学科交叉研究热点所反映出的对于相同问题的解决,各个学科会采用不同的学科理论,同时也会运用其他学科的理论帮助问题的解决。对于某学科早已形成的成熟理论被其他学科用来解决不同学科的问题,说明前者的理论得到推广和扩展,而后者找到了理论的源头,指导解决问题的研究,说明交叉融合的学科越多,解决问题所面对的角度也就越多。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




