1.HPM教学片段
此部分内容虽然是学生的课后拓展知识，但实际上它在前面的新课内容——必修5第一章第2节第4课时“三角形的计算问题”，及其例题、习题中已有所体现.所以它可以直接融入新课的学习过程中，也使得教学过程更流畅，学生的学习一气呵成.以下为具体的教学片段.
师：现在，我们已经推导出了三角形的三个面积公式，分别为：
也就是说，已知三角形的两边及夹角，便可直接利用公式求出三角形的面积.那么就请同学们利用公式计算教材16页的例7.
好，第（1）小题，已知两边,a b及夹角B，怎么做？
生：直接利用公式
师：代入得到S=
×23.5×14.8×sin148.5°≈90.9(cm2).那么第（2）小题，已知两角B,C与一边b，怎么办呢？
生：可以利用正弦定理！
师：很好，由正弦定理得：
在这里，由三角形的内角和可直接求出角A=180°-B-C=51.5°，所以代入得到：
于是我们得出了一个结论，已知两角和一边时也可以求出三角形的面积，只不过间接使用了正弦定理而已.
那么第（3）小题呢，已知三边长，怎么求面积？同学们好好思考一下.
生：利用余弦定理和正弦定理！
师：非常好，那我们一起来整理思路.现在已知三边，便可以利用余弦定理求出任意一角的余弦值.然后由三角函数的平方公式，对应角的正弦值也可求出，最后呢？
生：直接利用三角形面积公式!
师：那我们现在就一起来计算吧，不妨求角B的余弦值.
应用公式则有：
同学们，也就是说，已知三边也是能求出三角形的面积的！但是这个过程就稍微有点复杂了，计算也更加烦琐.那么我们想啊，能不能依照这个计算过程推导出一般的三角形面积公式呢？(www.xing528.com)
现在，已知三角形的三边长为,,a b c，求它的面积S.请同学们认真推导.
生：
师：对了，按照刚刚计算的方法，有
我们继续来化简，把
代入根号中，就有
其实，这就是著名的“三斜求积”公式！它是我国南宋著名数学家秦九韶在《数学九章》中独立推出的，目的在于利用此公式来解决古代田域的问题.所以说，秦九韶重实践重创新的精神，不仅推动了我国古代数学的进步，还帮助解决了当时的田耕问题，推动了农业的发展！
不过，最早推出由三边求面积公式的不是秦九韶，是古希腊的数学家阿基米德，公式也不是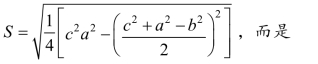
此公式被称为“海伦公式”，因为它最早被古希腊数学家海伦在其著作中记载，并给出了证明.那么同学们能不能再试着推导一下“海伦公式”呢？
（由于此公式的推导较难，所以主要由教师板书演练）
好，我们一起来推导：
现在，记
代入上式即为
同学们，现在我们推导出了我国的“三斜求积”公式和西方的“海伦公式”，以后这些公式可以直接应用于实际问题的求解过程中.虽然它们形式不同，但它们是等价的.可以看到，“海伦公式”的形式整洁，更便于我们记忆.现在就请同学们看着教材17页的例8，快速计算一下区域的面积.
生：利用“海伦公式”更简便！
师：是的，直接应用“海伦公式”可得到区域面积约为2840.8平方米.也希望同学们今后可以好好利用数学家们留给我们的宝贵财富，牢记他们所做出的杰出贡献！
2.教学分析
以上教学片段将“阅读与思考”中的材料融入了新课课堂，引导学生从教材例7第（3）小题的计算自行推出我国秦九韶的“三斜求积”公式.并讲解了它在古代数学中的作用，即解决了田域类问题，从而让学生感受到数学最根本的意义就是解决生活问题，推动社会发展.接着再给出西方与之等价的“海伦公式”，它的推导过程比较复杂，教师需慢慢引导学生，不能囫囵吞枣，只知结果，不解过程.
由于“海伦公式”的形式漂亮，便于记忆，能帮助学生更快捷地解决实际问题，故学生可直接应用于教材例8，进而让他们感受到数学家们的贡献是无价的，唤起他们的敬佩之情.
而教材上的编排是利用正余弦定理的交替使用以及三角形的面积公式来讲解这两道例题的，新课结束后再单独给出“海伦和秦九韶”的拓展内容.这里并没有去培养学生的归纳能力和解题能力，也没有利用数学史上这两大公式的简便性和实用性.所以相对而言，以上教学片段更好地去发挥了数学史的作用和学生的能力，还让他们感受到了数学成就的魅力和数学的应用意义.教材中的数学史料是值得我们深入课堂的，HPM教学也应立足于教材.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
