1.HPM教学片段
众所周知，“杨辉三角”是我国古代最璀璨的数学成果之一，课本利用它来学习二项式系数的性质，有趣又有效.
但是，“杨辉三角”的作用还不止这些，教材在本课之后的“探究与发现”中也提到了它的许多其他秘密.在新课教学中，我们也可以将其融入课堂，让同学们看到“杨辉三角”中蕴藏的更多的魅力.以下为具体的教学片段.
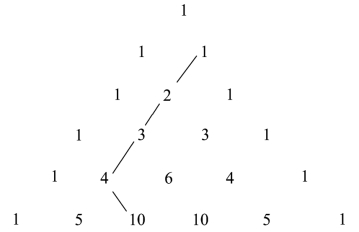
图7-11 探究一
师：前面我们学习了杨辉三角，也借助杨辉三角发现并讨论了二项式系数的一些性质.
而杨辉三角作为我国古代伟大的数学成果之一，它其中所蕴藏的奥秘还远不止这些.下面，我们继续来探究它的秘密.
同学们，观察图7-11中杨辉三角内部的连线，你们能发现什么规律？能不能归纳出一个一般性的数学结论呢？小组之间相互讨论.
生：
师：那可不可以证明呢？
生：可以，左边转化为1+2+3+…+n，即等于
师：很好，我们发现杨辉三角这一斜行之和的结论，能不能继续推广？
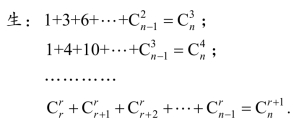
师：也就是说，现在我们得到了(www.xing528.com)
这个一般性的结论，怎么证明？
（同学们进行思考和讨论）
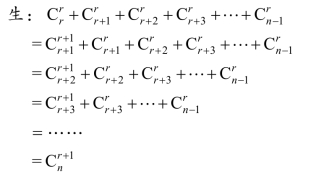
师：对了，正是利用我们前面所学的性质
来推导出来的.没想到杨辉三角不仅横看.竖看有秘密，斜着看也有秘密！
那我们继续观察，如图7-12所示，杨辉三角中的这些斜行，它们之间又有什么规律，你们能发现吗？请小组之间相互讨论.
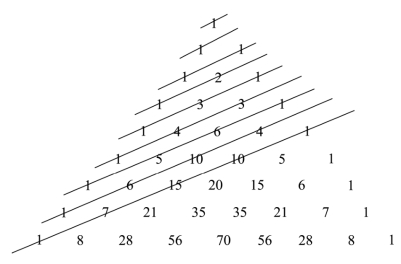
图7-12 探究二
生：每一斜行之和，排成一列即1，1，2，3，5，8，13，21，34…刚好就是斐波拉契数列!
师：是的，其实除了这些，杨辉三角中还蕴藏了许多数学知识，需要我们从不同的角度和方法观察所得，希望同学们可以在课后继续探究，领略杨辉三角更多的魅力！
2.教学分析
以上教学片段用于新课中，杨辉三角不仅可以观察二项式系数的性质，还可以通过其中不同形式的排列得到
以及斐波拉契数列等数学结论.当然，这些只是杨辉三角中的九牛一毛.此片段是基于教材中的课后知识“杨辉三角中的一些秘密”来展开新课教学的，在利用杨辉三角找到二项式系数的规律后，再和同学们一起探究出它蕴藏的更多奥秘，从而让同学们感受杨辉三角这个古代数学成就的了不起，引发他们的爱国之情和对民族的自豪感.
另外，在新课上探究更多杨辉三角的秘密，可以引起同学们对杨辉三角的探索兴趣和热情，以至于发现它所含有的更多数学规律和结论，从而培养同学们的发散思维能力和探索未知的数学研究精神.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
