毕达哥拉斯学派的三角形数和正方形数在高中数学教学中的应用

1.HPM教学片段

“形数理论”作为教学引入的确可以提高学生的兴趣.但是，数学史的应用不能只停留在“形”的表面.更多的时候，这些图形是帮助我们更形象直观地学习数列的知识.教材既然已经给出数学史料，我们便应该将它的作用发挥到极点，也让学生们感受到数学家们所做出的杰出贡献.

教材中，“数列的概念及其简单表示法”之后，紧接着讲解“等差数列”与“等差数列的前n项和”，利用高斯解决“1+2+3+…+100=?”的方法引入，再利用他的方法探究“1+2+3+…+n+…=?”的结果，从而得到一般的等差数列前n项和的求和公式：实际上，除了高斯方法，我们还可以利用毕达哥拉斯学派的“形数理论”去探究“1+2+3+…+n=?”的结果，甚至于它还能探究“1+3+5+…+(2 n-1)=?”和“2+4+6+…+2n=?”的结果，从而让同学们学会更多解决问题的途径，使其思维发散，锻炼其思维弹性.另外，在教材内容“等比数列的前n项和”的例3中，其边空备注知识延伸了公式但是课本中并没有给出证明方法，由于学生也还没有学过数学归纳法，难免会对公式产生疑惑.此时，若利用“形数理论”得以证明，既有助于他们对公式的学习，也有助于培养他们的解题能力.以下为具体的教学片段.

师：同学们，从高斯的算法中我们得到了启发，利用倒序相加的办法得到了等差数列1,2,3,…,n,…的前n项和，那么是否还有其他巧妙的办法得到前n项和的结果呢？大家还记得我们之前学过的毕达哥拉斯学派的三角形数吗？你们能不能结合它来得到呢？

（同学们认真地思考，并动手操作，有了倒序相加法的基础，有些同学便想到了再补一个倒三角形来解答.）

师：现在我们就一起来看看古希腊数学家们是如何求出1+2+3+…+n 的和的.同学们，假设现在用小石子摆一个有n行的三角形，请问总共耗费多少颗小石子呢？

生：1+2+3+…+n！

师：很好，需要用到1+2+3+…+n 颗石子，但是这个结果等于多少呢？我们继续用三角形数来探究，同学们知道怎么做吗？

（基于前面的思考和老师的点拨，同学们踊跃回答）

生：在原本的三角形旁边也摆上同样的倒立的三角形，补成一个平行四边形（见图7-4）！则有

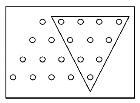
图7-4　两个三角形数的组合

2(1+2+3+…+n)=n(n+1)，

两个三角形数的和等于一个正方形数！

师：所以得到

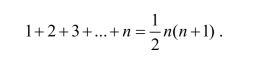
古人们也是像你们这样来解决等差数列1，2，3，…，n，…前n项和的！

同学们感受到形数理论的威力了吧，其实啊，形数理论的作用还不止这些呢！同学们再看看图7-5所示的正方形数.假设有n行n列，又能得到什么呢？

图7-5　正方形数的分割

生：1+3+5+…+(2 n-1)=n2!

师：对了，按照分割的办法，可以将一个n行的正方形数分成1,3,5,…,2 1n-，由此就得到了正奇数这个等差数列的前n项和啦.而对于正偶数的前n项和，同学们能不能也试着用n+1 行n列的长方形数来解决呢，把自己的草稿本当作沙滩，也来学习数学家们画一画.

（类比正方形的分割，很多同学都想出了办法）

好，许多同学都类比正方形的切割方法画了解决的办法，现在我们一起来看一看图7-6.等差数列2,4,6,…,2n,…的前n项和是多少呀？(www.xing528.com)

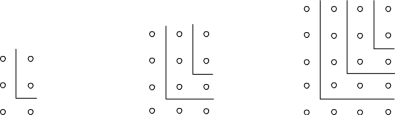
图7-6　长方形数的分割

生：2+4+6+…+2n=n(n+1)!

教学片段二：

师：同学们，现在我们知道了那么如何去证明这个结论呢？

现在，我们做出一个n行的三角形，将小石子画作圆圈，并在圆圈中填上数，第一行填上1，第二行填上2，第三行填上3，…，第1n-行的圆圈都填上1n-，第n行的圆圈都填上n，如图7-7所示.

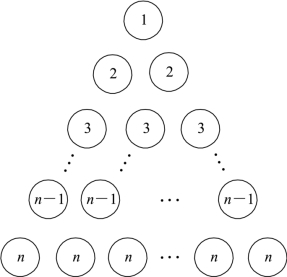
图7-7　第一个三角形

好，就像这样，我们得到这个正三角形之后，将其顺时针旋转120°，得到第二个三角形.圆圈中的数变成了从左往右每一排数依次为n,1n-,…,2,1，如图7-8所示.

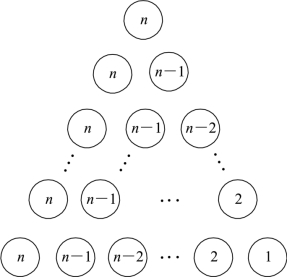
图7-8　第二个三角形

得到第二个正三角形后，再将其顺时针旋转120°，得到第三个三角形.圆圈中的数变成了从右往左每一排数依次为n,1n-,…,2,1，如图7-9所示.

图7-9　第三个三角形

现在，我们将这三个正三角形对应位置上圆圈内的数相加，则它们的和均为2 n+1，我们得到第四个正三角形.现在同学们能根据这四个三角形推导出二次幂和公式吗？如图7-10所示.

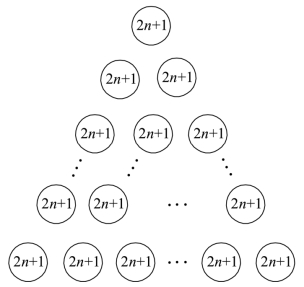
图7-10　第四个三角形

生：前三个三角形圆圈内的数相加之和为（3 12+22+32+…+n2），最后一个三角形圆圈内的数相加之和为由它们相等便有：

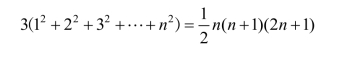
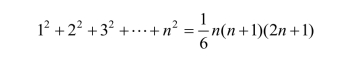
所以得以求证.

2.教学分析

以上教学片段均为教材中所出现的毕达哥拉斯学派的“形数理论”在人教A版数学教材“数列”一章的课堂应用.“形数理论”这个数学史料本身的特殊性，使得它在“数列”中的课堂活动有趣而丰富.它可以引起学生的兴趣，唤起学生的求知欲望，让他们学习用代数和图形解决数学问题，发展其开拓创新的数学思维能力.

我们也认识到了教材中的数学史如何根据教材编排的方式进入课堂，并通过“形数理论”的具体史料内容思考了更多进入课堂的方法，使得该数学史料不仅能用在引入方面，还能深入新课内容.这样学生便能学到更多的数学文化知识和应用方法，感受数学史的魅力，感受HPM教学的魅力.